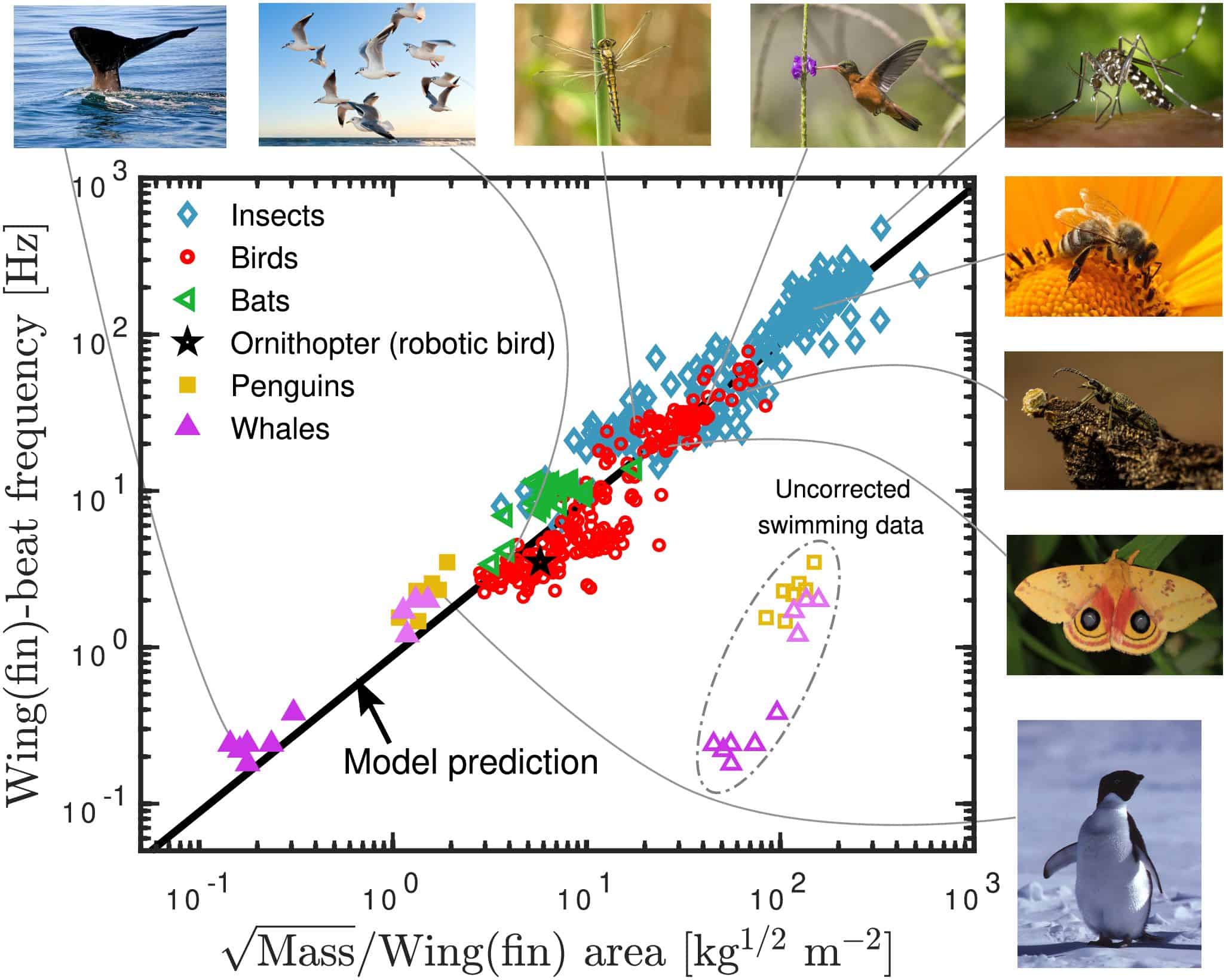
Whales gotta swim, and birds gotta fly – and when they do, they flap their wings and fins at a rate determined by the same simple mathematical expression and coefficient of proportionality. The expression, which relates wingbeat frequency to body mass and wing area, is valid regardless of the animal’s size or flying style, and the physicists who derived it say it matches biological data on insects, bats and flapping robots as well as birds and whales.
“We were surprised to see how well the data follows the prediction and kept expanding the data set to include other flying animals to see how far this universality goes,” says study leader Tina Hecksher of Roskilde University, Denmark. “When we saw that even swimming/diving animals follow the same line, we thought that this may interest a broader audience.”
Scientists have long searched for universal patterns in animal flight. In 1990, for example, the British biologist Colin James Pennycuick related wingbeat frequency f to a bird’s body mass and wing area via the expression f = 1.08(m1/3g1/2b-1A-1/4ρ-1/3), where m is the mass, g is the acceleration due to gravity, b is the wing span, A is the wing area and ρ is the density of air. His work followed that of the Australian mathematician and educator Michael Deakin, who in 1970 derived a simpler relationship for insects. Both analyses, however, were partly based on empirical observations, and neither sought to generalize them to other flying animals.
Dimensional arguments
The latest work was inspired by an exam question that asked students to explain how quickly a bird should flap its wings if it wants to remain hovering. The course was designed to teach students to “think like physicists,” Hecksher tells Physics World, and after the exam she and her Roskilde colleagues Jens Højgaard Jensen and Jeppe Dyre began to wonder whether the formula they derived using dimensional analysis would apply to real-world flight.
On the face of it, it might seem unlikely that any simple expression could capture much about an animal flapping its wings. Writing in PLOS One, the Roskilde team acknowledge that there is “obviously a significant difference” between the flight of a dragonfly and that of a bat, so past researchers had “good reasons” for focusing on similar species. Previous studies also showed that the shapes and angles a wing assumes during flight – which can be highly complex and vary widely across species – play a role in determining flapping rate.
Shapes and angles, however, are dimensionless quantities. The Roskilde physicists therefore folded these and other unknown dimensionless functions of dimensionless quantities into a single constant of proportionality. By hypothesizing that this constant must be the same for all flying animals, and ignoring minor variations in air density and gravitational field strength, they arrived at their expression: f ~ m1/2/A.
Empirical tests
To test the validity of this expression, the Roskilde team collected 414 data points from published studies that reported wing area, mass and wingbeat frequencies of birds ranging from swans to hummingbirds; flying insects such as bees, moths, dragonflies, beetles and mosquitoes; and a flapping robot called an ornithopter. The team also included data from whales and penguins. Unlike fish, which use air-filled bladders to regulate their position in the water, these animals have a positive buoyancy, and must swim to stay submerged. The physics governing their fin- and fluke-flapping frequencies should therefore be similar to the physics of wingbeat frequencies, barring a correction factor for the different densities of air and water.
When the Roskilde physicists plotted f against m1/2/A for all the animals (plus one robot) in their dataset, the result was a straight line with only a small amount of scatter in the data points. According to the team, this means that, despite huge physical differences, flying animals must have evolved in a way that keeps the relationship between their mass, wing area and wingbeat frequency relatively constant. “We were initially surprised that the data fall on the same line,” Hecksher says. “The basic relationship follows from physics. But the constant of proportionality could in principle be different for different flying styles.”
Matt Wilkinson, who did his PhD on pterodactyl flight and is now a director of studies in natural sciences at Cambridge University, UK, was also surprised, at first, that an analysis based on hovering, rather than forward flight, is so widely applicable. “There is a highly constrained relationship between wingbeat frequency and wingspan due to the enormous drop-off in efficiency when operating the wings away from their resonant frequency, but for larger flying animals, that frequency isn’t enough to support the animal’s weight on its own – some minimum forward velocity becomes essential,” he explains.

Through turbulent skies: how fluid dynamics experts are uncovering the secrets of bird flight
After some reflection, however, Wilkinson, who was not involved in the Roskilde study, suspects that this size-dependent factor “must be another phenomenon buried in the proportionality coefficient”. Identifying this coefficient is, he says, the study’s most important contribution. “Unpicking that, despite the enormous differences in wing shape and flight kinematics, is where the real insights will be found,” he concludes.
As for why no-one had uncovered this simple relationship before, Hecksher cites the study’s interdisciplinary nature. “Our formula is theoretically derived based on physics principles [and it] also devises how to compare swimming/diving animals in the same plot as the flying animals,” she notes. “This approach is less common among biologists…it takes the combination of physics and a large amount of empirical data to arrive at this result.”



