Randolf Pohl was not in a good mood, late one evening in July 2009. Sitting in a control room at the Paul Scherrer Institute (PSI) in Switzerland, he was cursing the data from a project he’d embarked on over a decade earlier. Known as the Charge Radius Experiment with Muonic Atoms (CREMA), it was designed to measure the radius of the proton more precisely than ever before. Technically very demanding, CREMA involved firing a laser beam at hydrogen atoms in which the electron had been replaced by its heavier cousin, the muon.

Pohl, who was then a postdoc at the Max Planck Institute of Quantum Optics in Garching, Germany, was trying to tweak the laser until its energy was just enough to excite these muonic hydrogen atoms from the ²S_1/2 to the ²P_1/2 levels. Quantum theory says that the energy difference between the levels, known as the Lamb shift, should depend ever so slightly on the size of the proton. The idea was to detect the X-rays emitted when the atoms were excited by the laser and decayed to a much lower energy level. The precise laser frequency at that point, combined with atomic theory, would then reveal the proton radius.

Unfortunately, having scanned what they thought was the entire frequency range corresponding to all possible radii, Pohl and his colleagues had come up empty-handed. There was no X-ray signal in sight. But then team member Aldo Antognini, who turned up for the night shift, had an inspired idea. He suggested looking at a range of frequencies seemingly ruled out by previous experiments, that CREMA had yet to explore. With potentially just a week of observation time left, the researchers quickly re-adjusted their equipment.

Amazingly, a signal emerged. Clearly visible above the background, it indicated that the proton’s radius is 0.84184 ± 0.00067 fm (where 1 fm = 10^–15 m). That made it nearly 4% smaller than the then official value set in 2006 by the Committee on Data of the International Science Council (CODATA) and, given the tiny error bars, completely at odds with it.

Puzzling times

The strange discrepancy between CREMA and previous measurements became known as the “proton radius puzzle” because it involved what appeared to be two contrasting but very well founded sets of results. On the one hand was the CODATA value, calculated on the basis of data from around two dozen experiments using two techniques: electron scattering and hydrogen spectroscopy. On the other was the CREMA result – a single, very precise spectroscopy measurement for which no obvious flaws had been found, either before or after the result’s publication in 2010 (Nature 466 213).

The disparity created great excitement among theorists, who speculated that it could be due to some previously unforeseen difference in the fundamental behaviour of electrons and muons. After all, the Standard Model of particle physics says that (apart from their masses) electrons and muons are completely alike. So if CREMA’s result was right, it raised the thrilling prospect that the Standard Model might need overhauling.

But excitement began to wane when theorists failed to find a new force that could explain the discrepancy. What’s more, by 2017 new results from the two kinds of traditional proton-radius experiments started to confirm the muon data. CREMA’s famous result now appeared not as a harbinger of revolution in physics but as a wake-up call that the earlier scattering and spectroscopy measurements had gone badly wrong. More remarkable than the discrepancy, however, was the way that new measurements from those traditional techniques seemed to fall in line – as if the field underwent a collective U-turn.

Wim Ubachs of Vrije Universiteit in Amsterdam, who is not part of CREMA, admits to being baffled by this “peculiar matter”, as he puts it, but stresses he has the “highest esteem for the people involved in the field and would not want to point to any wrongdoing or manipulating of data”. Pohl himself says that systematic errors in the earlier work must be to blame, though he is unable to identify the culprits. “It’s very strange that so many experiments could be wrong in the same way,” he says.

Others, however, think the mystery may not be all it’s cracked up to be. Some nuclear physicists even dispute the idea that researchers had no inkling of a smaller radius until CREMA came along. Among those is Ulf Meißner at the University of Bonn in Germany, who says he had first started arguing for a lower value for the proton radius in the mid-1990s. “There was a clear discrepancy,” he recalls. “But for whatever reason CODATA was always sitting on the high value.”

Indeed, the saga raises questions about how the values of the fundamental constants ought to be decided and what role CODATA should play. For Meißner, the decision-making is not transparent and depends too much on certain individuals’ tastes. “It is more psychology than physics,” he claims.

Narrowing the gap

CODATA was set up by the International Council for Science in 1966 to organize and preserve the increasing volumes of data produced by scientists around the world. It entrusts the delicate task of setting the values of nature’s most basic parameters, such as the Planck constant, electron mass or gravitational constant, to the Task Group on Fundamental Constants. Consisting of 15 or so scientists from around the world, the group usually adjusts those values every four years using the least-squares method to fit them as closely as possible to available experimental and theoretical results.

For most constants, this process is not ambiguous as different results agree among themselves within the limits of their error bars. That much seemed true when the task group first published an official value of the proton radius – or, more specifically, the average radius of the proton’s electric charge – in 2002. At that time, the radius was derived from the two more conventional types of experiment. Electron scattering measures the extent to which high-energy electrons are deflected by hydrogen nuclei (protons). Ordinary spectroscopy, meanwhile, compares the measured frequencies of one or more electronic transitions in hydrogen with the values predicted by quantum electrodynamics (QED) to obtain a value for the Lamb shift and with it the proton radius. The figure CODATA settled on in 2002 was 0.8750 ± 0.0068 fm, which changed only slightly four years later, remaining a little under 0.88 fm.

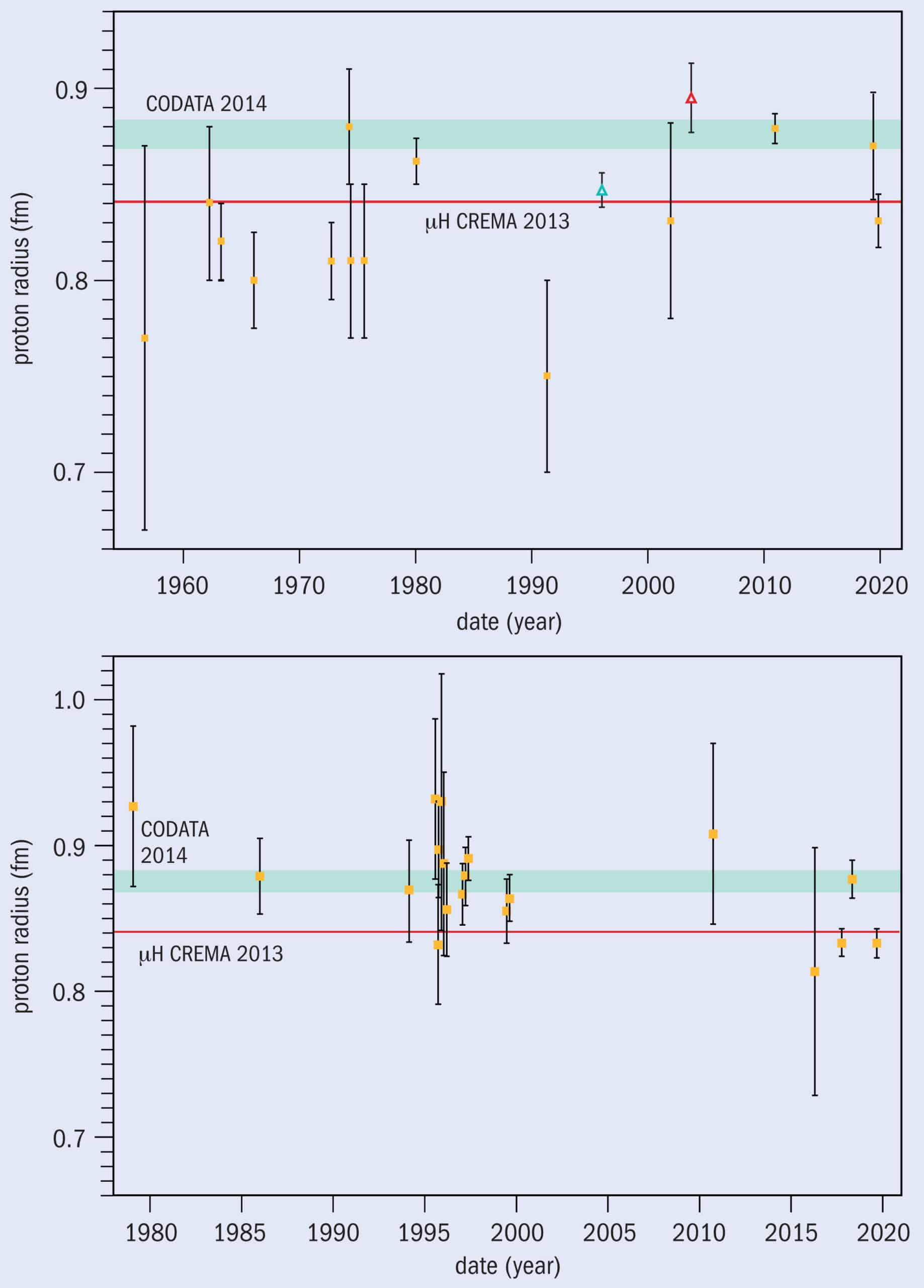
But in 2010 along came CREMA with its muonic hydrogen spectroscopy measurements. The advantage of using muons is that they are about 200 times heavier than electrons and so get closer to the proton than their lighter counterparts, making the Lamb shift more pronounced. The resulting value of around 0.84 fm was far more precise than the official number, but the CODATA task group decided to stay put. It omitted the muon data from its 2010 adjustment, partly because new, improved scattering data from the MAMI accelerator at the University of Mainz in Germany agreed with the bigger radius. And four years later the group did the same thing when its members met up in Paris. Even though a number of invited speakers had argued it was getting ever harder to identify any experimental or theoretical loopholes that could explain away the CREMA results, the group voted – by a count of eight to two – to again exclude the muon data.

It was only in 2018 that the panel changed its approach. By then, several experimental teams had either published or communicated new data from conventional hydrogen spectroscopy agreeing with CREMA – including one at the Max Planck Institute (comprising Pohl) and another at York University in Toronto, Canada. With CREMA itself having published an even more precise value of the proton radius, the task group finally incorporated the muon data. The value that emerged from its best fit that year was very similar to the muonic one alone, but with bigger error bars: 0.8414 ± 0.0019 fm.

Decisions, decisions

In deciding what to do with conflicting data, the CODATA task group aims to be neutral. Peter Mohr, a physicist from the US National Institute of Standards and Technology who chaired the group from 1999 to 2007 and is still a member, explains that it incorporates all “individually credible” results and then takes an average. “[It] does not decide whether particular data are right or wrong,” he says. “This would require superhuman powers.”

However, the panel’s handling of the proton radius raises questions. Mohr says it “made less sense to average” the large and small radii in 2014 than it did four years later, given the absence of independent confirmation at that time. But why it changed tack in 2018 is not clear. According to the minutes of that year’s meeting, again held in Paris, the panel considered recent results from conventional spectroscopy to be “inconclusive” given that, alongside the support for a smaller radius, researchers at the Kastler Brossel Laboratory in Paris again obtained the higher value when measuring hydrogen’s ¹S–³S transition.

Mohr defends the group’s decision-making process, maintaining that the situation with the proton radius was “not all cut and dried”. He and his colleagues decided ultimately to change the value, he explains, given a “preponderance of evidence” in favour of the smaller number. But he admits that the statement about the hydrogen spectroscopy results in the 2018 minutes was “poorly worded”.

Others, however, offer a different interpretation. Despite being “close to 100% convinced” in 2014 that the small radius was correct, Pohl, who gave a talk at the meeting that year, says he nonetheless supported retaining the high value. That approach, he felt, would keep the spotlight on the proton-radius puzzle and motivate further work to try and resolve it. Indeed, Simon Thomas from the Kastler–Brossel Laboratory in Paris also thinks that CODATA wanted to keep the question alive rather than obtain the most precise possible value of the radius.

As he notes, the CREMA result was not really at odds with individual spectroscopy experiments – all but one differed by no more than 1.5 standard deviations, or σ. The only significant disparity – of at least 5 σ – arose when the conventional data were averaged and the error bars shrunk. But that disparity could only be maintained if the muon result itself was kept out of the fitting process – given how much it would otherwise shift the CODATA average towards itself.

Thomas sees nothing wrong with the task group drawing attention to the puzzle rather than simply opting for the most precise values of the constants. (Indeed, Pohl reckons “no-one cares” about the exact value of the proton radius apart from spectroscopists.) He also regards the consequent boost in research funding as a necessary and healthy part of the scientific process. “It is only when both scientific and strategic motivations coincide that they [scientists] take a stance on a result,” Thomas says

A black box

It’s debatable whether the task group has always been so enthusiastic about bringing inconsistencies to light. Indeed, some nuclear physicists reckon it did just the opposite before the muon data emerged – having ignored scattering data pointing to a smaller radius (see box below). The result, they say, was a high value of the radius that appeared more solid than it really was.

The task group’s approach did not change even after CREMA published its initial muon data. In 2014 it called on “two pairs of knowledgeable researchers” to extract a value from the scattering data. These were Ingo Sick from the University of Basel in Switzerland teaming up with John Arrington of the Argonne National Laboratory in Illinois, and Michael Distler and Jan Bernauer from the University of Mainz, Germany. With both pairs calculating a high value, the scattering radius continued to be large – about 0.88 fm.

But, as before, others had arrived at a different conclusion. Douglas Higinbotham of the Thomas Jefferson National Accelerator Facility in Virginia and colleagues showed they could use linear and other simple extrapolation of low-momentum data to work out the radius, rather than the higher-order polynomials favoured by Sick and others. Their work yielded a value consistent with CREMA – indeed, they argued that “the outliers” were not the muon or scattering results but those from ordinary (rather than muonic) hydrogen.

The task group mentioned this study and two others favouring the smaller radius in its 2014 report, but dismissed them on the basis of a critical analysis by Bernauer and Distler. That pair identified what it claimed were “common pitfalls and misconceptions” in the other groups’ statistical analyses, arguing in the case of Higinbotham and co-workers that they had misunderstood tests used to justify lower-order extrapolations.

Higinbotham sees things differently. He maintains that the use of extrapolations based on higher-order polynomials “makes no mathematical sense”, adding that nuclear theorists have in fact been using dispersion relations to obtain a low value of the radius since the 1970s. But he complains that no-one from the small-radius camp was interviewed by CODATA in 2014. “It can be tough when you feel you are not getting the opportunity to discuss your point of view,” he says.

Meißner compares the task group’s approach unfavourably with that adopted in particle physics, where the international Particle Data Group, he says, lists all competing values of constants and lets users make up their own minds. CODATA’s decision-making process is, he argues, more “like a black box”, with the panel including or excluding data on the basis of “personal decision” rather than objective criteria. Indeed, Mohr has “to confess to not remembering” why the group relied so heavily on Sick’s analysis (with no explanation appearing in its various reports).

As to the use of Bernauer and Distler’s critical analysis in 2014, he says the task group was presumably “persuaded by their arguments”. But why no explanation of that choice? “That becomes a political question I guess,” he replies. “Evidently we trusted those people but to go into details about why we trusted them I can’t give concrete arguments.”

End game

Whether a different treatment of the scattering data could have ushered in a smaller proton radius before CREMA found its signal, or at least raised the uncertainty of the large value, is a moot point. Distler argues that the data simply weren’t precise enough to clearly distinguish between two different sizes, while Meißner thinks the discrepancy would have been less pronounced come 2010 but cautions that his view is “pure speculation”.

The task group itself noted in its 2010 report that, with the scattering data removed, the discrepancy between conventional and muonic results dropped from a whopping 7 σ to just 4.4 σ. Under those circumstances, Thomas reckons that the disparity would still have raised the same questions about a possible crack in the Standard Model, but would have generated much less media coverage. “I think there would still have been a puzzle, only a little less famous,” he says.

Scientists naturally continue searching for systematic errors when a result disagrees with what they expect but otherwise might not try quite so hard

As to what caused the presumed but still unidentified errors in conventional spectroscopy, Thomas suggests that scientists naturally continue searching for systematic errors when a result disagrees with what they expect, but otherwise might not try quite so hard. Or, in the words of Jean-Philippe Karr, a fellow atomic physicist at the Kastler–Brossel lab, “People are serious and continue looking, but maybe they are a bit less motivated when they are at the right value, so to speak.”

To try to work out what might have pushed up the result from their ¹S–³S measurement, Thomas and colleagues are studying the same transition in deuterium, which could reveal any missed systematic errors due to atoms’ finite velocities. Similar work is also being carried out by the group at the Max Planck Institute, which last year reported very precise measurements of the transition in hydrogen using a frequency comb – again obtaining the small proton radius.

Nuclear physicists too are busy. Researchers at the Jefferson lab are currently preparing an upgrade to the Proton Radius Experiment, having in 2019 reported a small radius in 3 σ disagreement with results from other scattering efforts. The MUSE experiment at the PSI, meanwhile, is preparing to scatter both electrons and muons off protons to establish whether the two types of lepton might behave differently after all.

In fact, there are some who continue to argue for a large proton radius. Distler, whose colleagues at Mainz are also planning fresh experiments with lower systematic errors, insists that the group’s existing results are valid. He maintains that the mismatch with the muonic data might only be apparent, and that it could be due to incomplete hydrogen energy-level corrections from QED – stemming perhaps from the production of multiple particle–antiparticle pairs. “It would mean we have two values of the radius and both would be right,” he says.

Meißner, in contrast, has no doubt that the small radius is correct. He says he doesn’t want to take anything away from the CREMA researchers, describing their experiment as “really high accuracy and great stuff”. But he resents what he regards as the lack of credit given for his work beforehand, while admitting that he can’t discuss the proton radius anymore with his counterparts at Mainz. “They can take the large value of the radius to the grave,” he says. “I don’t care.”