Samuli Siltanen explains how solving an “inverse problem” will improve the quality of life of people who can’t speak and have to use voice synthesizers – particularly women and children, whose only current option is to sound like an adult male

The première was only 30 minutes away, and my voice was alarmingly hoarse. I had come down with a common cold just as I was supposed to play the role of the devious pilot Yang Sun in Bertolt Brecht’s The Good Person of Szechuan. Our enthusiastic amateur theatre group had been practising the piece three times a week for months, and I hated the prospect of having to cancel our first public performance. Luckily, one of the cast was a doctor, and she gave me a shot of industrial-grade cough medicine. Within minutes my voice had made a miraculous recovery, and I followed through with the 90-minute vocal ordeal.
The next day, however, I couldn’t utter a word – no sound whatsoever. My regular doctor instructed me to stay completely quiet for 10 days to let me heal my vocal folds – those twin flaps of mucous membrane in the larynx that vibrate to create sound when air is forced through them. My enforced silence caused surprisingly many inconveniences. The worst was that my wife couldn’t help thinking I was mad at her, despite knowing full well that I wasn’t giving her the “silent treatment”!
What this episode illustrates is that spoken language is simply such an integral part of our everyday experience that it is hard to imagine life without it. For me, my temporary lack of voice was a minor inconvenience, but sadly there are many people who are not able to speak at all. For some of them it is a disability they were born with, while others end up with no voice as a result of a stroke, an accident or cancer.
Although the spoken sounds we utter every day are effortless to produce, they are actually extremely complex
Fortunately, it is possible to help speech-impaired people with technological aids. And in this digital age we can do far better than the infamous bicycle horn of Harpo Marx. We can programme computers to turn text input into audio output, as evidenced by Stephen Hawking’s speech synthesizer. However, mimicking human speech is not as easy as it might seem. Although the spoken sounds we utter every day are effortless to produce, they are actually extremely complex. Communicating is not only a question of what you say but also a question of how you say it, and the how part is based on very subtle nuances.
It is these human-like how features that are very difficult to design into text-to-speech algorithms. In other words, it is hard to make computers speak with versatile and natural-sounding emotional content. Another problem is that it is tricky to synthesize a woman’s or a child’s voice – as these have a higher pitch than men’s voices – meaning that many women and children who have lost their voice have to use a speech synthesizer that sounds like a man.
Computer-generated speech
Designing and programming good speech-synthesis software is a daunting task. The most straightforward approach would be to record a huge collection of sample sounds, Each word would be read by a person at several pitches, with different emotional content – angry, loving, happy, strict and so on – and possibly for several dialects. Each word would need to be spoken by women, men, girls and boys, and for each language we wish to synthesize.
This method has its drawbacks, however. Consecutive samples do not necessarily fit well together, resulting in unnatural-sounding speech, while the processing power and computer memory required may make portable devices impractical.
An alternative approach, which is computationally more efficient, is to first analyse and understand speech by dividing it up into its structural components and then to synthesize each of these. This method, which Hawking uses, lets him control many aspects of speech, such as melody, rhythm and intonation, all of which are important in distinguishing statements from questions and for expressing emotion.
There are many mathematically and computationally challenging aspects of this method. In my research I focus on generating vowel sounds, which is hard but at least it suffices to model “static” sounds. Synthesizing consonants is even harder since it always involves dynamical, fast-changing features.

A vowel sound consists of two independent ingredients. The first is the sound produced by the vocal folds flapping against each other, known as the glottal excitation signal. (The vocal folds and the gap between them are called the glottis.) The second ingredient is the modification of this sound by the vocal tract, which is the curved and intricately formed air space between the vocal folds and the lips.
Let’s try a simple musical experiment to demonstrate. While the suggested performance may not hit the charts, it illustrates the independence of the two components of a vowel sound. First, sing “Mary had a little lamb” with all the words replaced by “love”. This shows that the same vowel can be uttered using an arbitrary pitch (well, within some limits, obviously). Second, sing the words “sweet love” at the same pitch as each other. This demonstrates how the pitch can be kept the same while singing two different vowels.
The pitch of a vowel sound is measured in hertz and is the number of times the glottis closes in a second. The vocal folds are actually the fastest-moving parts of the human body, with the pitch of a typical male voice being between 85 and 180 Hz, and that of a female voice from 165 to 255 Hz. The pitch of the vowel sound comes solely from the glottal excitation signal.
As the “sweet love” example above shows, even when two different vowel sounds have the same pitch it is very easy to distinguish between them. The same goes for notes of the same pitch played by different musical instruments – think of how easy it is to tell the difference between a piano and a saxophone playing the same note, for example.
This quality of the sound that makes it identifiable – often referred to as the character or “timbre” – is best studied in the frequency domain. The simplest sound, known as a pure tone, contains only one frequency. The glottal excitation signal contains all frequencies equal to or higher than the pitch of the signal. However, the shape of a vocal tract modifies this signal to create a complex tone, in which some of these frequencies are damped and others emphasized to create a unique sound.
Figure 1
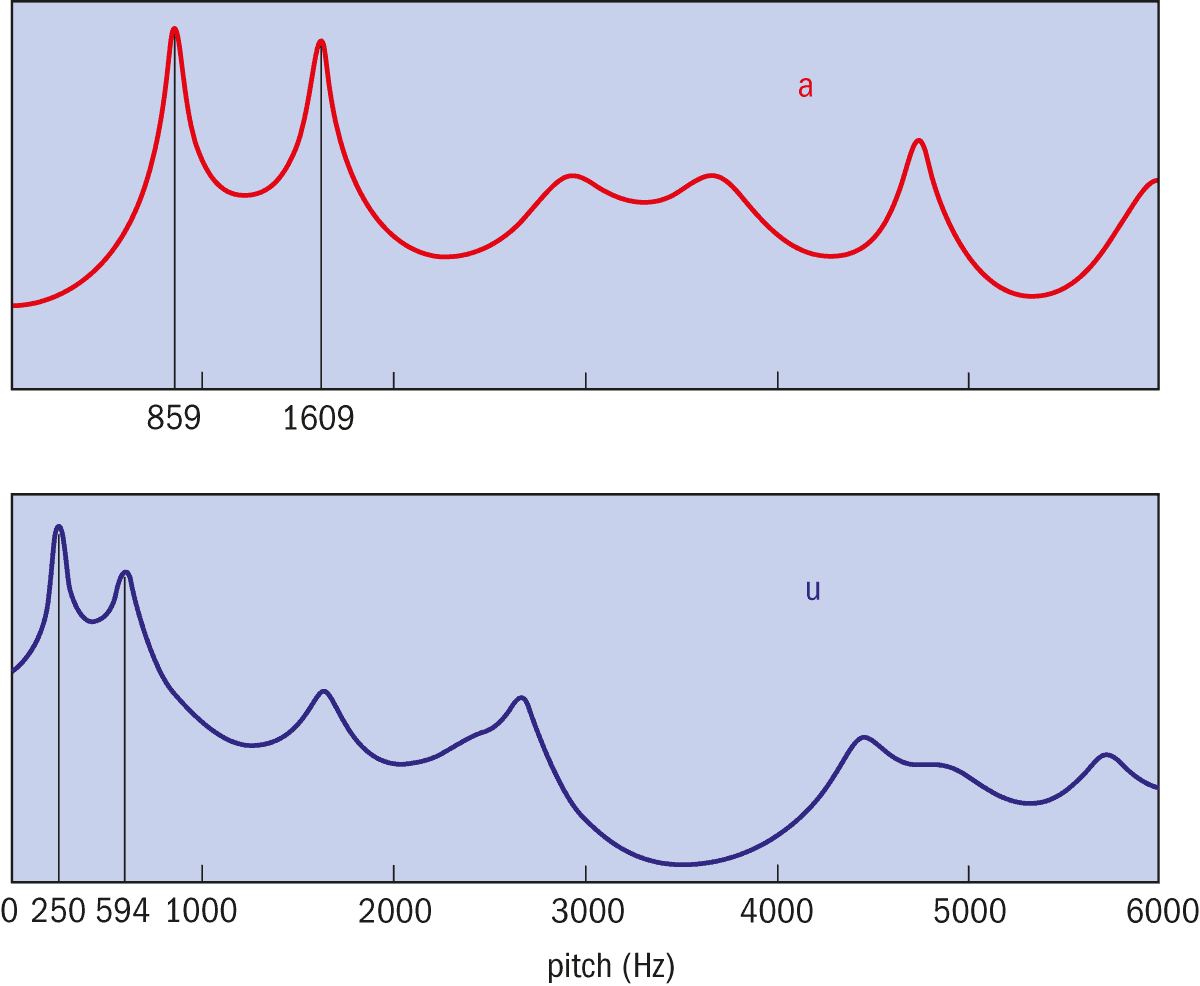
When people make vowel sounds, such as “a” in the word “car”, and “u” in the word “rule”, the effect of the vocal tract can be neatly observed in the so-called frequency domain. Similarly to a frequency equalizer on 1980s home stereos, the vocal tract emphasizes some frequencies and damps others. The most prominent frequencies are called the formants and define which vowel sound is being made. As shown here for example, the first and second formants for “a” are 859 Hz and 1609 Hz, while in “u” they are 250 Hz and 594 Hz.
Figure 1 shows examples of two vowel sounds in the frequency domain. Each vowel has two specific frequencies that are strongly emphasized, seen here as the two highest peaks: the so-called first and second formants. To make a particular vowel sound, muscles in the tongue, mouth, throat and larynx activate to give the vocal tract a particular shape in which these two formants resonate. You can observe a similar resonance when singing in a shower cubicle: certain notes seem to vibrate the whole bathroom, while others do not.
Creating natural-sounding vowels
To generate natural-sounding synthetic vowel sounds using a computer, we use a simple model for both the glottal excitation signal and the shape of the vocal tract. The excitation signal is described by a mathematical formula giving the amount of air flowing through the glottis at any given time (figure 2). Regarding the vocal tract shape, in the simulations we use circular tubes of varying radii, creating life-sized models of them for demonstration purposes (see the photo higher up this article). While these forms are far from the true anatomical shapes, they produce surprisingly natural vowel sounds.
Figure 2
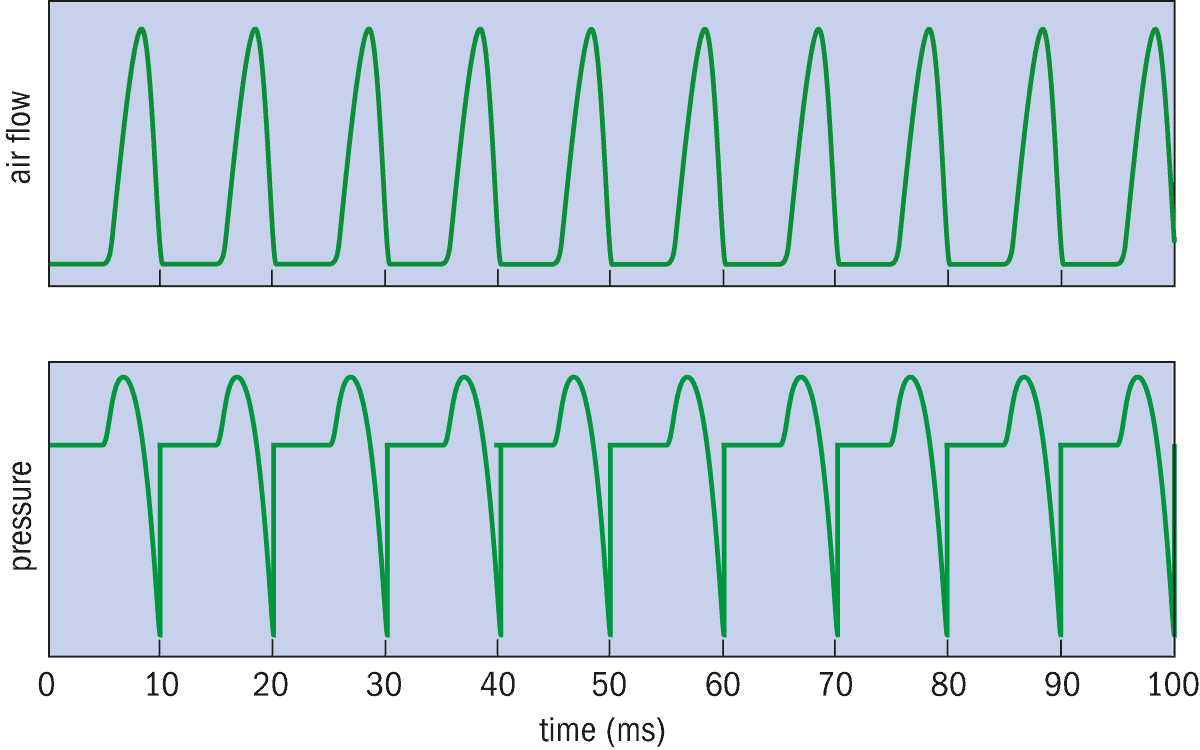
In our synthetic speech simulation at the University of Helsinki we simulate the periodic airflow through the glottis as a function of time, here with a pitch of 100 Hz (top). The vocal folds periodically flap against each other and every closure of the glottis brings the airflow abruptly to zero. Vital for our model is the pressure in the vocal tract as a function of time, known as the glottal excitation signal (bottom), which is calculated as the derivative of the airflow.
Good-quality synthetic speech needs natural samples of glottal excitations and shapes of vocal tracts. Those things are difficult to measure directly. The glottal excitation signal can be roughly recorded using a microphone attached to the Adam’s apple, and the shape of the vocal tract can be imaged using magnetic resonance imaging. It would be much nicer, however, if one could recover all that information simply from regular microphone recordings of vowel sounds. This in turn requires solving an inverse problem.
As with many inverse problems, the measurement data are not enough on their own to uniquely determine the cause
An inverse problem involves trying to recover a cause from a known effect. It is a bit like a doctor trying to find out the reason why a patient has joint pain, a cough and a fever: there are several different conditions that could lead to those symptoms. As with many inverse problems, the measurement data (i.e. the symptoms) are not enough on their own to uniquely determine the cause (i.e. the illness). Therefore, enough a priori information – such as ongoing epidemics, season and weather, the patient’s history of illness – has to be added in order to arrive at a correct solution. (A forward problem, incidentally, involves simply going from cause to effect: if the patient is known to be infected with an influenza virus, then the doctor can easily and reliably predict joint pain, a cough and a fever.)
A roulette of vowels
The inverse problem my collaborators and I are studying is called glottal inverse filtering (GIF). The starting point is a short vowel-sound recorded with a microphone and given to the computer in digital form. The aim of our method is for the computer to output a glottal excitation signal and a vocal tract shape that together produce as closely as possible the original vowel sound. The recovered excitation signal and vocal tract shape can then be used separately in many other combinations to produce a wide variety of different vowel sounds.
A simple trial-and-error approach would not work, as there are several different combinations of excitations and tract shapes that produce very closely the recorded vowel sound: in that case the effect is right but the cause, or structural components of the vowel, are wrong.
The GIF method we have developed is kind of a refined, probability-driven, trial-and-error procedure, which uses Bayesian inversion implemented as a so-called Markov chain Monte Carlo (MCMC) approach. As this gambling-related name implies, MCMC involves generating random values, which we like to think of as spinning a roulette wheel. (See the box below for more on this general method.)
For each vowel sound that we are trying to simulate, our MCMC-GIF method produces a long sequence of vowel sounds – typically 30,000 of them. The sequence is created using a random process subtly geared so that the average of all the 30,000 sounds in the sequence will be a nice solution to the inverse problem.
The gearing of the random process goes like this: the first sound in the sequence can be freely chosen. From then on, the next sound in the sequence is always defined either by accepting a candidate sound or rejecting the candidate and repeating the previous sound in the sequence. The candidate vowel sound is randomly picked by “spinning the roulette wheel”, or choosing a random glottal excitation signal and a random shape for the vocal tract. It is accepted only if it has high enough probability judged by the known measurement information (how close the candidate sound is to the original microphone recording) and the a priori knowledge (e.g. that the formants of the candidate are not too far from those of a typical vowel “a”).
Synthesizing speech by solving an inverse problem
In simulating speech using computers, we need to solve something called an inverse problem to produce natural-sounding vowels. This mathematical problem involves starting with a vowel sound and figuring out from it the initial conditions that led to that sound, i.e. the frequency at which the vocal tracts vibrated and the shape of the vocal tract.
To illustrate how this method works, here is a simple example in which we estimate the age of an imaginary girl, Jill. Suppose we have a recently taken, badly focused photo of Jill blowing out the candles on her birthday cake. It seems that there are 10 candles, but we cannot say for sure. This is our noisy measurement information: the number of candles is 10, give or take a few. We can model the uncertainty using a Gaussian bell curve centred at 10 and having a standard deviation of, say, three years.
We also have a priori information: say we know Jill won a medal in the under 32 kg division of the last International Open Judo Championship. The historical record of medallists gives empirical probabilities: for example, there is a 4% chance that Jill is 9 years old and 13% chance that she is 11. Also, from the championship rules we know that she is definitely at least 8 and at most 15.
Let us now construct a sequence of numbers that are estimates of Jill’s age. The first number is 10 – the apparent number of candles on Jill’s birthday cake. To determine the next number we spin a hypothetical roulette wheel and call the result (a randomly picked number between zero and 36) the “candidate”. Now we either accept the candidate and add it to the end of our sequence, or reject it and instead repeat the last number in the sequence.
So how do we choose whether to accept or reject the candidate? What we do is to calculate the probability of the last number in the sequence and the probability of the candidate – the latter being the product of the photo-based probability (the Gaussian bell curve centred on 10) and the judo-based probability (given by the historical percentage). If the probability of the candidate is higher than the probability of the last number in the sequence, we accept the candidate. If the candidate is less probable, we do not reject it outright but rather give it one more chance. For example, if the probability of the candidate is a third of that of the last number in the sequence, we spin the roulette wheel again and accept the candidate only if the wheel gives a number smaller than or equal to 12 (which is a third of 36).
Finally, the average of the sequence of numbers generated with the above randomized method is an estimate for Jill’s age. The longer the sequence of numbers we generate, the better estimate we get.
Of course, in our simulation we’re not trying to compute an age but the frequency and vocal-tract shape that led to a certain vowel sound (see main text).
Voice of the future
Before our new method, there were no clear samples available of high-pitched excitation signals that women and children could use for natural-sounding synthetic speech. That’s because traditional methods are unable to solve the inverse problem for high-pitched voices – they cannot separate the excitation signal and the filtering effect of the vocal tract from each other. This means that the only option for many women and children is to use a speech synthesizer with a man’s voice.
In our work, we show that the probabilistic MCMC-GIF method can recover glottal excitation signals and vocal tract shapes more accurately than traditional GIF algorithms, even for voices with high pitch. Once these new computational advances are put in place, women and children will therefore be able to express themselves via computer-generated speech better suited to their identity. We hope that, as a result, quality of life will be improved for women and children who have lost their voice.
Our new method is still in the research phase in the sense that it is computationally quite expensive. However, now that we have demonstrated that it works, we are working on the next step – using mathematical techniques to speed it up. Once this is achieved we will be able to offer it to speech-synthesizer companies, who can then make the technology available.