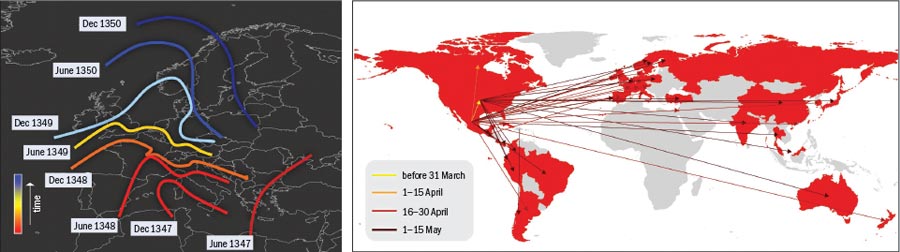
The Black Death was one of the most devastating pandemics in history. Beginning in 1347, the plague took just three years to spread from Constantinople in western Turkey to Italy and then on to the rest of Europe, leaving nearly a quarter of the continent’s population dead in its wake. Historical studies confirm that the disease diffused smoothly, generating an epidemic front that travelled through the continent as a continuous wave at a rate of about 200–400 miles per year.

In 14th-century Europe few means of transport were available and travellers could cover only relatively short distances in a day. The advent of modern transportation has dramatically altered this picture, speeding up disease transmission significantly. For example, the influenza pandemic of 1918 took just one year to spread from its US or European source to isolated Pacific islands, while the 1957 flu virus swept the globe in about six months.

On 11 June 2009 the World Health Organization (WHO) declared that a new virus, known as H1N1 influenza or “swine flu”, had become the first pandemic of the 21st century. This time, only two months passed between the first international alert and the WHO’s announcement. From a scientific and public-health perspective, such rapid transmission posed an unprecedented challenge: we and other groups working at the interface between physics, epidemiology and computational science needed to track the evolution of the pandemic in real time. Under these circumstances, there is a large degree of uncertainty in what will happen. How fast will the virus spread to new countries? What will be the impact on the population? How dangerous is it? And, most importantly, what weapons do we have to fight it?

As an interconnected, mobile society, we face a number of disadvantages in combating pandemics. Fortunately, we also have some advantages over our predecessors. These include not only significant progress in medical science, but also a powerful new epidemic-fighting weapon: computational models derived from network science, mathematical epidemiology and the statistical physics of reaction-diffusion processes. In the words of evolutionary biologist Andrew Dobson, models are now “as crucial in the study of infectious diseases as are microscopes, stethoscopes and the tools of molecular diagnosis”.

Models can be used to assess the impact of epidemics and pandemics on human health, and to predict the geographical spread of a disease, the expected number of cases and the timing of an epidemic’s peak. Numerical results from these models can help alert health officials, guide planning for social-distancing measures like school closures, and suggest strategies for the development, production and administration of vaccines. They can also allow public-health experts to assess the impact that all these interventions might have in mitigating the pandemic.

The role of physics

Physicists have long used computational approaches to solve problems involving a large number of degrees of freedom, and can now simulate material processes and physical phenomena on a wide range of scales. It is now almost routine to study, say, fracturing processes in materials by simulating over a billion atoms or to solve evolution equations for six billion finite elements in plasma fluids. Furthermore, the advent of ab initio, Monte Carlo and other simulation techniques in areas such as quantum chemistry, molecular dynamics and materials science has made it possible to calculate the behaviour of single atoms or aggregate states of matter from first principles.

Given these successes, it is natural to wonder why we are at a far more primitive stage in the quantitative forecasting of how newly detected emerging diseases (or even seasonal influenza) will evolve. The basic difference is that even though the simulation of six billion human beings is in principle computationally feasible, the models used in epidemic and contagion processes have to include social and behavioural factors, not just the (comparatively simple) physical laws governing fluids or atomic motion. So, while the theoretical foundation required to approach the spread of diseases computationally has been in place for a long time, progress has been hindered by a lack of data on how people interact, travel and behave – as well as on how communities are structured, and how they react to environmental, political, technological and cultural factors. All these layers – from the single individual to the global society and its surrounding environment – interact at multiple scales, thereby increasing the complexity of the phenomena to be modelled and creating formidable obstacles to the development of predictive computational approaches.

The last decade has, however, witnessed a sharp increase in our capacity to gather these data. This is mostly because the boundaries between real-world social behaviour and the cyberworld have started to disappear. Devices like mobile phones and personal digital assistants produce detailed traces of our daily activities. Websites have sprung up to record data, such as the dispersal of banknotes that can be used to infer human interactions and mobility, as shown by Dirk Brockmann and co-workers (see page 31, print edition only). This huge mass of data is changing our understanding of a wide range of phenomena by producing quantitative descriptions of large-scale social systems.

As a result of this data revolution and increased computer-processing power, researchers are now beginning to integrate large-scale datasets into models of mathematical epidemiology. This means that we are finally in a position to move from analysing the “social atom”, or small social groups, to analysing “social aggregate states” made up of millions of people. But in making this transition – which is equivalent to the shift from atomic and molecular physics to the physics of bulk matter – we must confront the complexity of the system that emerges from the collective behaviour of a large network of interacting units.

Networks that trace the activities of individuals, social patterns, transportation fluxes and population movements all exhibit large-scale non-uniformity that emerges spontaneously as the system evolves. The statistical distributions characterizing the fluctuations in these networks are generally “heavy-tailed”, meaning that their standard deviations are extremely large – there are no “typical” values for many of the quantities of interest. For example, the distribution that defines the probability that each node in the system (representing anything from an individual to a country, depending on the model) is connected to k neighbouring nodes is often approximated by a power-law decay. This indicates that there is an appreciable probability that some nodes may have orders of magnitude more connections than the “average” value of k for the system. A similar pattern is also observed for the intensity of the flow between connecting links, transport flows and other basic statistical quantities characterizing the network structure.

Our ability to deal with such systems – where the behaviour at any scale is the outcome of a complicated interplay among processes that occur on very different time and length scales – places an important constraint on efforts to model emerging infectious diseases. Fortunately, some of these same difficulties have already been addressed in physical systems that feature phenomena such as turbulence or critical behaviour (“tipping points”). Tools that were developed for these problems, including renormalization-group techniques, timescale-separation approaches and homogenization methods are therefore viable candidates for addressing the new challenge of pandemic modelling.

Network-based models

The network perspective itself is also creating new mathematical tools and approaches. Both physicists and epidemiologists have recognized the importance of network structure in the spreading of diseases in a globalized world and have developed models that explicitly integrate multiscale mobility networks into the description of emerging diseases. For example, although the spread of the Black Death can be adequately described mathematically using continuous differential equations with diffusive terms, in modern times the spread of epidemics is mainly determined by the human-mobility networks that allow infected people to travel across continents in less than a day (see “Speed of epidemic propagation”). The current swine-flu pandemic, therefore, cannot be simply described in terms of diffusive phenomena but must explicitly incorporate the spatial structure and deep interconnectedness of today’s modern society.

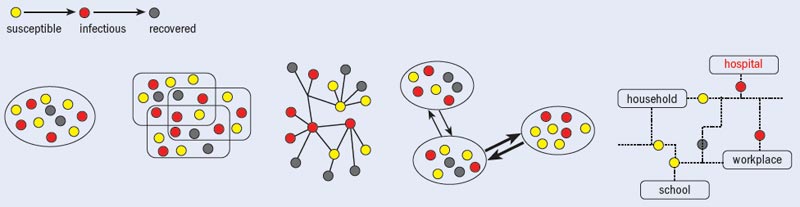
In recent years, two major classes of models have emerged that are particularly useful for simulating influenza-like illnesses (see “Model approaches”). The first, known as the agent-based approach, keeps track of each individual in a population in an extremely detailed way. Agent-based models typically take into account the fact that infection can spread among individuals by contacts between household members, school and workplace colleagues, and by random contacts in the general population. One key feature of such models is that they characterize the network of contacts among individuals based on the socio-demographic structure of the population.

The second scheme relies on meta-population models that consider the long-range mobility of people at an inter-population level, while using coarse-grained techniques at the level of individual interactions. In such models, the world is divided into geographical regions that define a sub-population network. Connections among each sub-population represent the fluxes of individual humans due to the transportation infrastructure. Infections evolve inside each urban area, and this process is described by schemes in which the discrete, stochastic dynamics of the individuals in different compartments depends on the specific causes and origins of the disease and any containment interventions.

Of these two techniques, agent-based models provide a large amount of data, but their computational cost and – most importantly – the need for very detailed input data has, to date, limited their use to a few country-level scenarios. The structured meta-population models, in contrast, are fairly scalable and can be conveniently used to provide worldwide scenarios and patterns. Although the level of information that can be extracted is less detailed than in agent-based models, the spatial and temporal ranges, and the number of realizations that can be computationally analysed, are all much larger.

Modelling a pandemic in progress

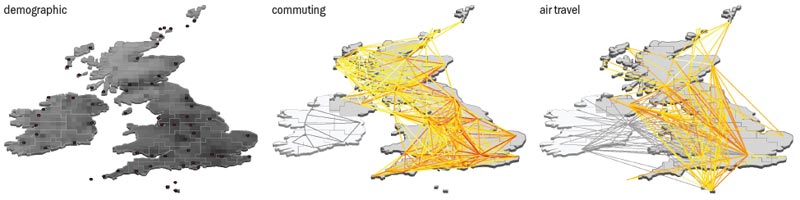
While the recent growth of computational epidemiology laid the foundations for a first-principles approach to modelling epidemics, the swine-flu pandemic represents the first time that such computational methods have been used to model the spread of an infectious disease in real time. So far, the results have been extremely encouraging: state-of-the-art, large-scale computational approaches have been able to capture the spatio-temporal pattern of the unfolding epidemic quite accurately, making projections up to three weeks in advance. In particular, it has proved possible to anticipate which urban areas or countries will observe the first local cases of the disease, and thus become “hotspots” of the epidemic. Remarkably, different methodologies – including the Northwestern University group’s proxy networks and our own approach, which is based on the integration of real transportation and mobility data (see “The GLEaM model”) – provide very similar patterns and results. This indicates that the basic elements considered in the models – population distribution and human-mobility networks – are able to capture the main features of the epidemic’s evolution.

The integration of large-scale mobility networks into epidemic models is also providing new ways to estimate the virus’ transmissibility and other basic parameters of the epidemic. Disease transmissibility, for example, is usually indicated by the mean number of secondary cases that a typical infected individual generates in a population with no immunity. This quantity is often estimated using temporal data on the number of cases detected in each country. However, the accuracy of these data depends on whether cases are spotted and properly reported to health authorities, and as a result they sometimes give a very misleading picture of an evolving epidemic. For example, several studies indicated that the official number of swine-flu cases reported by the authorities in Mexico, where the virus was first identified in April 2009, had underestimated the actual impact of the epidemic by a factor of 100–1000.

Using the mobility-network approach, we can instead calculate transmissibility using data on the first handful of cases detected in newly affected countries. These data tend to be more accurate. This new approach is possible because the chronology of the infection of new countries is determined by two factors: the number of cases generated by the epidemic in the originating country; and the mobility of people from this country to the rest of the world. The mobility-network data are defined from the outset with great accuracy, and we can therefore determine the parameters of the disease by calculating which values best fit the computational-model results for the chronology of infection in new countries. This strategy has already been used by the WHO Rapid Pandemic Assessment Collaboration, Harvard University epidemiologist Marc Lipsitch and co-workers, and by our own group to provide independent early estimates of the transmissibility of the swine-flu pandemic virus and the cumulative incidence in Mexico.

Another notable success for this strategy was that we were able to predict several months in advance that the swine-flu pandemic in the US and the northern hemisphere would peak between late October and late November 2009. Being able to anticipate such peaks is crucial for testing possible vaccination scenarios, since the effectiveness of mass-vaccination campaigns depends on having vaccines available at the right time and in the right place. In this context, data-driven computational models can shed light on the fuzzy pandemic future, and serve as in silico experiments on the effectiveness of mitigation strategies.

More to be done

The swine-flu pandemic has shown that computational tools can be used successfully and considered as a support tool in the complicated decision-making process of public-health policies. Yet even before the current pandemic started, simulation results had already fundamentally altered our understanding of the interplay between social behaviour, infrastructures and the biological processes of infectious diseases. Thanks to analysis performed by Deirdre Hollingsworth, Neil Ferguson and Roy Anderson at Imperial College London; the computational approaches of Ben Cooper and Joshua Epstein (based at the UK Health Protection Agency and the Brookings Institute, respectively); and our own analytical and simulation work, by 2006 researchers knew that travel restrictions alone would do little to contain or even slow down a global epidemic. Using reaction-diffusion techniques, we were able to show that the topology of the air-transportation network and the traffic flow through it meant that unless traffic restrictions were more than 90% effective, they would not delay the peak of a pandemic by more than two to three weeks. And, of course, such a drastic reduction in air travel would quickly lead to social and economic disruption.

The same interconnectedness that makes draconian travel restrictions impractical also reduces the effectiveness of any containment or mitigation strategies that are limited to a single country. A traditional strategy for epidemic control assumes that drugs will be used in the very few countries in the world capable of amassing stockpiles, but in a highly connected world such localized mitigation is not as effective as a coordinated global strategy. If wealthy countries are willing to share a very small fraction of their stockpiles of antiviral drugs with developing countries, in contrast, this would hugely mitigate the impact of a pandemic.

In some ways, computational approaches to the spread of epidemics are remarkably similar to the sophisticated simulation methods used in physics. In both cases the “social atoms” interact, move and react in constrained spaces. The final aggregate state (the social system and its epidemiology) is the outcome of the principles governing these microscopic processes. However, a major difference has to be factored in. Unlike a physical system, the unfolding of the epidemic is going to affect the individual’s behaviour. Indeed, even the model predictions themselves – along with news about the epidemic that is transmitted via a variety of media sources – could affect the choices people make, like deciding to travel less. This social adaptation to the available information is part of the dynamic of the system. Paradoxically, the model’s reliability produces, through its predictions, a feedback on the model itself.

This issue is still uncharted territory. Current models focus largely on situations where steady-state data are used to study the system under normal conditions, in which the social behaviour is not altered or disrupted. The next challenge is to develop formal models that can deal with the prediction–adaptation feedback loop and the possibility of their validation. This is something that goes beyond the physics of fluids, gases and particles, or the “physics” of non-adapting social atoms. And it is where a truly interdisciplinary collaboration among physicists, epidemiologists, computer and social scientists is inevitably needed.

At a glance: Modelling epidemics

• Modern pandemics spread more quickly and less uniformly than in the past, thanks to the global air-transportation network and the complex and interconnected nature of our society
• Modelling the spread of new infectious diseases requires theoretical and computational models that take into account physical and biological principles plus social and behavioural factors
• A range of new tools for simulating influenza-like illnesses has been developed in recent years, allowing researchers to predict how events like the current H1N1 flu pandemic will evolve

References

R M Anderson and R M May 1992 Infectious Diseases of Humans: Dynamics and Control (Oxford University Press)
D Balcan et al. 2009 Multiscale mobility networks and the spatial spreading of infectious diseases Proc. Natl Acad. Sci. USA 106 21484–21489
D Balcan et al. 2009 Seasonal transmission potential and activity peaks of the new influenza A(H1N1): a Monte Carlo likelihood analysis based on human mobility BMC Medicine 7 45
D Brockmann, L Hufnagel and T Geisel 2006 The scaling laws of human travel Nature 439 462–465
V Colizza and A Vespignani 2007 Invasion threshold in heterogeneous metapopulation networks Phys. Rev. Lett. 99 148701
B S Cooper et al. 2006 Delaying the international spread of pandemic influenza PLoS Med. 3 e12
J M Epstein et al. 2007 Controlling pandemic flu: the value of international air travel restrictions PLoS ONE 2 e401
N M Ferguson et al. 2006 Strategies for mitigating an influenza pandemic Nature 442 448–452
C Fraser et al. 2009 Pandemic potential of a strain of influenza A(H1N1): early findings Science 324 1557–1561
T C Germann et al. 2006 Mitigation strategies for pandemic influenza in the United States Proc. Natl Acad. Sci. USA 103 5935–5940
M C Gonzalez, C A Hidalgo and A-L Barabási 2009 Understanding individual human mobility patterns Nature 453 779–782
M E Halloran et al. 2008 Modeling targeted layered containment of an influenza pandemic in the United States Proc. Natl Acad. Sci. USA 105 4639–4644
T D Hollingsworth, N M Ferguson and R M Anderson 2006 Will travel restrictions control the international spread of pandemic influenza? Natl Med. 12 497–499
M Lipsitch et al. 2009 Use of cumulative incidence of novel influenza A/H1N1 in foreign travelers to estimate lower bounds on cumulative incidence in Mexico PLoS ONE 4 e6895
S Riley 2007 Large-scale transmission models of infectious disease Science 316 1298–1301