Six decades after the discovery of DNA’s double-helix structure, the molecules that make up the genetic code are still revealing some fascinating twists. Davide Marenduzzo, Cristian Micheletti and Enzo Orlandini explore the physics of DNA knots

Knots are very much a part of everyday life. In some cases, they are extremely useful: sailors and climbers, for example, need them for their own safety or to secure boats and equipment. But in other cases, knots are a nuisance. You may have found this yourself the last time you tried to reel in a long extension cable after, say, vacuuming your attic or mowing the lawn. Invariably, there is a knot in the cable when you want to store it away, and in order to un-knot it, you need to repeatedly pull one of its ends through the entangled region – a rather dull and lengthy procedure, as anyone who has ever tried to untangle headphone wires or Christmas tree lights can confirm.
The theory of how knots form, and how different knots can be distinguished, began as a rather abstract mathematical discipline. Developed by a trio of Scottish physicists – Peter Guthrie Tait, James Clerk Maxwell and William Thomson (later Lord Kelvin) – in the late 19th century (see September 2010 pp35–40), it was originally intended to support the now-abandoned idea that atoms might consist of knotted tubes of aether. Since then, however, physicists have also found practical applications for knot theory. One important example concerns the possible configurations of DNA molecules. Like extension cables, the filaments that make up DNA can become knotted in all sorts of ways, and research into the kinds of knots formed by DNA is telling us some interesting things about the molecule’s properties.
For example, one might imagine that DNA knots will make it difficult for proteins to read, transcribe and replicate the knotted portion of the molecule. Excessive DNA knotting can even prevent cell division and lead to cell death. Moreover, the DNA inside bacteria and human cells is so long (millimetres and metres, respectively) that one would expect to observe knots very frequently. However, certain enzymes, known as topoisomerases, have evolved to solve this problem by cutting DNA and gluing it back together. On the other hand, within some very small viruses, where there is space only for the DNA itself, knots are inevitable because of the tight confinement – yet the knots that form do not stop the virus from infecting its host. A better understanding of DNA knots may therefore give us some insights into these important cellular processes.
Loose ends
Before going into more detail about DNA knots, we first need some basic information about knot theory. Knots are grouped according to the minimum number of crossings they contain, and each knot in a group is given a number. For example, the simplest non-trivial knot, the trefoil knot, is known as 31: it has three crossings, and it bears the subscript 1 because it is the first and only possible knot with three crossings. Figure 1 shows representations of the trefoil knot along with several other simple knots. Note that in diagrams like these, it is crucial to retain information about which segment is on top at a crossing. For instance, if you flip the top and bottom segments in just one crossing of the trefoil knot, the resulting curve no longer contains any knots at all: it has become an unknot (0).
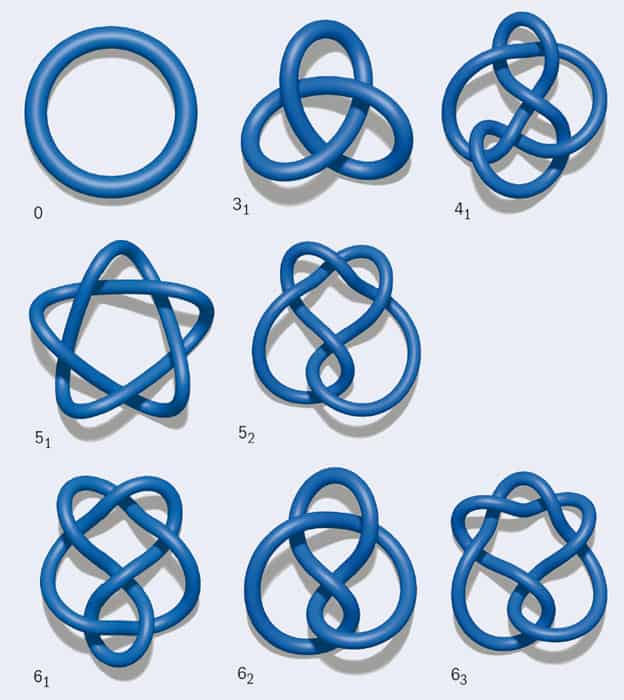
Now imagine trying to draw a knot as a closed curve on a surface. If the surface is a sphere, such as a balloon, the only knot that can be drawn without any self-intersections is the unknot. However, if the surface has the topology of a torus, such as a doughnut or a bagel, an infinite number of knots can be drawn on it (figure 2). These are called torus knots, and examples include the trefoil and 51 (cinquefoil) knots.
A second important family of knots is twist knots. To create one such knot, take a rope and hold it fixed at its two extremities. Then take the middle of the rope and twist the whole loop an integer number of times. Soon, the rope should start to look like a heavily used office telephone cord, a phenomenon known as “supercoiling”. Finally, take one of the ends, pass it through the top loop of the rope, and then link the ends so that the rope is now knotted. By increasing the number of twists, you can create a trefoil (which, notably, is a twist knot as well as a torus knot), a figure of eight (41), a three-twist (52) or a Stevedore’s knot (61).
Of these two families, twist knots are more commonly found in nature. This is because when unravelling a twisted cord, it is easy to inadvertently pass one end of the cord through a loop – and the same is true if some natural process rather than a human is doing the unravelling. A more rigorous way of saying that twist knots are easy to produce is to note that their “unknotting number” is 1. The unknotting number is the minimum number of times that a knot must be passed through itself in order to untie it. Equivalently, it is equal to the minimum number of crossings that must be flipped to obtain the unknot. With just a bit more drawing and thinking (and perhaps the aid of your headphone wires), it is fairly easy to show that the unknotting number of a 51 torus knot is 2. This knot is more difficult to form by mistake, as the cord has to pass through itself twice, rather than once.
A new twist
Based on these arguments, it seems logical to suspect that DNA molecules will frequently form twist knots, and that 52 twist knots will appear much more frequently than 51 torus knots. But how can this hypothesis be tested? After all, a DNA molecule is only about 2 nm (2 × 10–9 m) wide. When it is inside a cell or in solution, it occupies a space measured in microns; within viruses, it is even more compact. Given the tiny size of such a molecule, how can we determine which knots have formed in it?

Of course, it is possible to obtain images of a particular knotted DNA molecule directly, using electron microscopes. But if we want to know the probabilities of forming different types of knots – the “knot spectrum” – we need information about an entire population of molecules. One way to obtain this knot spectrum is through simulations. DNA molecules in solution can be made to form loops (by making their loose ends attractive to one another), so we can model them as fluctuating looped elastic rods, the bending rigidity of which matches that of DNA.
However, it is also possible to determine the knot spectrum experimentally thanks to a rather clever trick. DNA molecules are negatively charged, so one can use a weak electric field to drive them through a dilute substance called agarose gel, which is a jelly-like material filled with microscopic holes (a bit like a squishy bath sponge). As one might expect, small DNA molecules will pass through these holes more quickly than large and cumbersome ones, since bigger molecules become tangled up with the polymers that make up the agarose gel. In a simple model, one can treat the velocity of the DNA molecule in the gel as being inversely proportional to the size of the sphere that best approximates the molecule’s average shape. If the DNA under consideration is highly knotted, it will be crumpled up and smaller in size, so it will move more quickly through the gel than it would if it were unknotted. Remarkably, it is possible to separate knots with up to roughly 10 crossing numbers by looking at how fast they move in agarose gel – the first group of molecules to pass through the agarose will have 10 crossings, the next nine and so on.
This measurement technique enabled researchers to confirm in the 1990s that in solution, looped DNA molecules a few microns in length do indeed form twist knots, and that “simpler” knots with lower unknotting numbers are more probable (see, for instance, V V Rybenkov et al. 1993 PNAS 90 5307). Indeed, the statistics of the knots formed in the simulations and in the experiments are pleasingly very similar, which suggests that DNA loops could potentially be used as a test bed for probing ideas on knot theory.
However, a new twist in the field of DNA knots arrived in 2005 when Javier Arsuaga and collaborators studied DNA knots in a type of virus called a bacteriophage. Also known as phages, bacteriophages (literally “bacteria eaters”) are viruses that infect bacteria. They work in a remarkably simple fashion. Using a molecular motor, phages tightly pack DNA in their interior so that it reaches almost crystalline density. The phage then exploits the high pressure that results from this tight packing to fire the DNA into the cytoplasm of its bacterial host as soon as the protein shell containing the phage DNA (the capsid) is “untapped”.
One might naively expect that knots would be a bad thing
The only difference between phage DNA and the previously studied DNA in solution is the degree of confinement, which is much more dramatic in phages since they are so small: about 40–70 nm across. But does this confinement affect the knots that can form within the capsid?
The research of Arsuaga et al. suggests that it very much does: they found that knots occurred far more frequently in the phage DNA than in “unconstrained” DNA in a solution. More specifically, in natural or “wild-type” infective phages, about half the DNA molecules were found to be knotted. The researchers also discovered that the viral DNA often contained torus knots, while twist knots were virtually absent – quite unlike the pattern observed for DNA in solution.
Do these results tell us something more about DNA structure, at least within phages? To find out, it was necessary to extend existing models of fluctuating elastic loops to the case in which the loops are confined within a sphere of radius R – which, to be relevant for the case of phage DNA, must be much smaller than the contour length of the DNA molecule itself. These simulations did reproduce the intuitive result that confinement increases the likelihood of forming knots: the DNA molecule in the narrow space of the phage has more opportunities to cross itself several times, so knots can readily form. However, the simulations were unable to reproduce any bias in favour of torus over twist knots and, unlike in experiments, the number of 52 twist knots observed was always larger than the number of 51 torus knots. Moreover, when R was set to a realistic value of 25 nm, the DNA configurations found by simulations were very disordered and the knots formed very complicated, with far more crossings than found experimentally.
Was the disagreement between simulation and experiment the result of an incomplete understanding of DNA–DNA interactions within the bacteriophage? Or was the bias in favour of torus knots a result of some other effect – such as the “molecular motor” inside the phage, which may rotate the DNA while it is packaged, thereby potentially affecting its conformation?
Our group, as part of an interdisciplinary collaboration, found a possible answer to this question in 2009, when we simulated the packaging and ejection of DNA molecules inside a modified type of phage called a P4 cosmid (PNAS 106 22269). Though still infective, cosmids are mutants that contain only half the genome of the natural, wild-type phage. This makes them more treatable computationally, and experiments have shown that the knot spectra of P4 and P4 cosmids are qualitatively similar. To create our simulated DNA segments, we began with the fluctuating elastic rod models described earlier, but added an extra ingredient: the new simulations contained an “orienting” interaction between model DNA segments that kicked in whenever two segments got close to each other. This orienting interaction was designed to favour a small twist angle between the contacting segments. You can think of it as like the interaction that occurs when two chiral, corkscrew objects, such as pieces of fusilli, lock at an angle when forced into close contact (figure 3a).
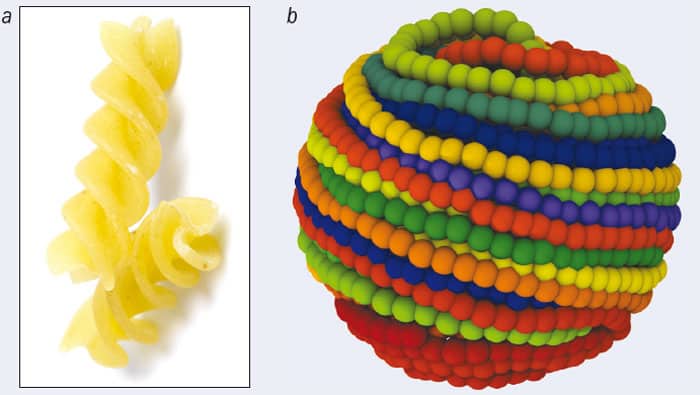
For the fusilli, the origin of the orienting interaction is geometric. For DNA, it may be mainly electrostatic, but whatever its ultimate origins, the effects of adding this interaction to our models were dramatic. When we used realistic values of parameters such as DNA rigidity (inferred from studies of DNA liquid-crystalline phases in solution), the simulations showed that, to begin with, the DNA inside the phage capsid is now ordered into a spool-like structure (figure 3b). This agrees with previous models for DNA packing and with electron microscopy pictures of phage DNA. Importantly, the twist knots are now strongly suppressed, and the knot spectrum is much more compatible with the experimental one.
Another knotty problem
While the puzzle of the twist knot absence was perhaps solved, another big question remained. One might naively expect that knots would be a bad thing for phages, because in order to be infective, they need to eject DNA from their interior into a bacterium, and the presence of knots might cause the DNA to get stuck. So how could the P4 phage have highly knotted DNA and still be infective?
A final answer to this question is still pending, but simulations suggest that the explanation may have to do with the concept of “knot localization”. If you tie a knot in a string and pull it tight, the knot will eventually localize such that it occupies a certain small region. But for DNA confined within a phage, our simulations suggest that the opposite happens: the knot delocalizes, spreading out over the whole DNA filament. In other words, the knottedness becomes a global property of the curve, one that cannot be captured by looking at a small fraction of the molecule.
This is crucial, because during the DNA ejection process, it is exactly the dynamics of such a small fraction (specifically, the bit that is close to the opening in the phage capsid) that dictates the physics of the process. If the knot is delocalized, this fragment will look no different for a torus knot than it will for an unknot, so simulations show that DNA ejection should proceed at approximately the same speed as it would if the molecule contained no knots at all. One can imagine further that torus knots may provide another advantage during ejection, as their toroidal (spool-like) geometry means that they may be readily unrolled, avoiding the formation or accumulation of self-entanglement – much as a spool helps prevent fishing lines from becoming tangled.
In bacteria, by contrast, knot localization seems to have beneficial effects. DNA molecules in bacteria are usually negatively supercoiled: in other words, the DNA helix is twisted less than it would be in a “normal” or undeformed strand, where the helical pattern repeats every 10 base pairs. Negative supercoiling is advantageous for the bacterial cell because it weakens the DNA helix, making it easier to break the hydrogen bonds keeping the helix together – something the cell must do whenever it “unzips” the DNA helix in order to transcribe and replicate it. But negative supercoiling may also help the bacterial cell remove problematic DNA knots. This is because if a knot happens to develop in a supercoiled strand, it normally becomes tight and localized, as shown in recent research by Guillaume Witz and collaborators from various institutions in Lausanne, Switzerland. This presumably makes it easier for the knot-removing topoisomerase enzyme to find, since the enzyme is attracted to regions of high DNA curvature.
The general picture we are developing is that in bacterial and human cells, DNA knots create many more problems than they do in viruses. Hence, control of these knots is very important, and we have discussed how topoisomerase enzymes have evolved to remove them. Usually, the removal of knots is a good thing, but in some circumstances we might actually prefer the DNA to remain knotted. For example, drugs that inhibit the functioning of topoisomerase enzymes have been used to treat cancer, because they prevent cells from dividing. So while topology and knot theory have already provided us with important insights into the physics of phage DNA, if we can uncover even more of the mysteries of DNA knots, it might open up new perspectives in biotechnology or even medicine. But before we get there, a lot more work has to be done.