Carbon is about to join the list of ferromagnetic elements, but the origins of its magnetic properties remain a mystery, say Michael Coey and Stefano Sanvito

Ferromagnetism, that most mysterious of the common properties of solids, has long known its place in the periodic table: down among the transition metals. These elements, which include iron and cobalt, have a net magnetic moment in the solid state because their atoms contain unpaired electrons. One of the last places you would expect to find ferromagnetism is in carbon, because its electrons love to pair up to form covalent bonds. These bonds are the antithesis of magnetic order, so how can we explain the increasing number of reports of magnetism in carbon?
Quantum mechanics links magnetism inextricably with the intrinsic angular momentum or “spin” of electrons. However, unlike classical angular momentum, which can take on any value, the spin of an electron can have only one of two values: “up” or “down”. Electrons therefore behave like tiny magnetic dipoles, and atoms have a net magnetic moment, m, if they contain more spin-up electrons than spin-down electrons, or vice versa. This often happens if the atom contains partially filled electron shells. However, matters become more complicated in the solid state.
Depending on the way the spins of different atoms in a material couple together, their magnetic moments can lead to a magnetically ordered state below what is known as the Curie temperature. Above this temperature the order is destroyed by thermal fluctuations. These exchange interactions, J, between the spins lead to two distinct phases in a solid depending on their sign: a ferromagnetic phase where the electron spins all point in the same direction, or an antiferromagnetic phase where alternate spins point in opposite directions.
Our current description of magnetic order is based on this “m–J” paradigm, but recent observations of magnetism in certain forms of carbon are stretching this picture to its limits. Furthermore, magnetic carbon could be used to make cheap, metal-free magnets for applications in medicine, nanotechnology and telecommunications, and also offers the prospect of carbon-based electronics.
Magnetic inventory
Normally the only elements that are ferromagnetic at room temperature are iron, cobalt and nickel, joined by gadolinium if the weather is not too hot. A few other rare earth elements, the “4f” series, become ferromagnetically ordered at lower temperatures, and almost all of these elements have a ferromagnetic or antiferromagnetic “ground state” at sufficiently low temperatures. Chromium and manganese, which lie in the “3d” series, are also antiferromagnetic. These series represent electron shells in the atom, which determine the overall structure of the periodic table. The innermost “1s” shell holds up to two electrons, the “2p” shell holds up to six electrons, and the 3d and 4f shells can hold 10 and 14 electrons, respectively (figure 1) .
Many useful ferromagnetic or antiferromagnetic materials are alloys of the 3d metals. Some examples are silicon steel (which is used for electromagnetic machinery), nickel iron (magnetic shielding and sensors), neodymium iron boron (high-performance permanent magnets), and iridium manganese (spin valves and magnetic tunnel junctions). The rest are oxides of the 3d elements, which have a slightly different “ferrimagnetic” order and include iron oxide (magnetic tapes) and barium iron oxide (fridge magnets and small motors).
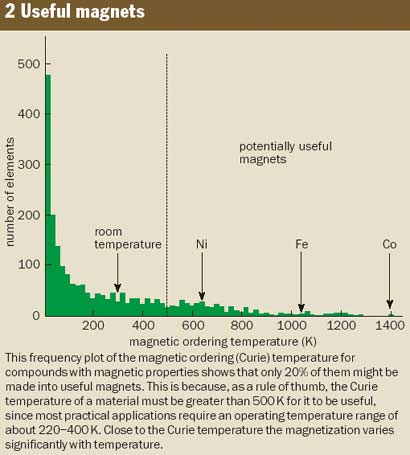
Besides these useful materials, of which no more than about a dozen are manufactured in industrial quantities, there are thousands of others that are known to have a magnetically ordered ground state. However, most of these compounds have relatively low Curie temperatures, and the chances of finding a useful new magnetic material – i.e. one that retains its order above a temperature of 500 K – is less than one in five (figure 2). Magnetic materials involve numerous chemical combinations of the 3d and 4f elements, but the overwhelming majority of magnetically ordered alloys and compounds include magnetic elements from two “islands of stability” in the periodic table. One island encompasses the 3d series and a few 4d elements, and the other includes the 4f series and a few 5f elements (see figure 1).
So where does all this leave carbon? Not only is carbon the most covalent of the elements, it is not even magnetic in the atomic state since the spin and the angular momentum of its six electrons cancel to produce a net magnetic moment of zero. Given such anti-magnetic tendencies, carbon hardly seems likely to become the ferromagnet of the future. Yet, at a glance, the magnetic periodic table suggests that there may be a third island of magnetic stability in the region of oxygen.

This is because elements such as oxygen can have a magnetic moment when they form molecules, as the molecular orbits form a spin triplet in their ground state. Drops of liquid oxygen, for example, are easily deflected by a permanent magnet, and solid oxygen orders in a complex antiferromagnetic structure when it is cooled below 44 K. Is oxygen an isolated case, or can its neighbours in the periodic table also form spin-triplet molecular states that order magnetically?
Reports of magnetic carbon
There have been a number of reports of magnetism in carbon, mostly in Russian and Japanese chemical literature. The idea is that various organic molecules can produce a ferromagnetic, carbon-based material after they have been heated in a vacuum. However, these reports have largely been ignored by physicists interested in magnetism, perhaps because the researchers were unaware of them but more likely because the results seemed implausible and were not readily reproducible. How could carbon possibly be magnetic?
The main cause for suspicion was that many of the reports claimed to have detected only small magnetic moments, which can simply be due to traces of natural magnetic contaminants. Iron, for example, is the fifth most common element in the Earth’s crust, and its black oxide magnetite is everywhere in the air. The magnetization of iron and magnetite are 220 and 100 A m2 kg-1, respectively, so a sample magnetization of 10-3 A m2 kg-1 or less can be easily dismissed as the consequence of magnetic contamination at the level of a few parts per million. Unfortunately, it is moments of just this magnitude that are often reported.
It is also difficult to separate these small moments from the underlying “diamagnetism” of carbon. This is a very weak form of magnetism exhibited by almost all forms of carbon (and, indeed, by many other elements) in the presence of an external magnetic field. The external field alters the orbital motion of electrons and induces a small magnetic moment in a direction opposite to that of the field itself. For insulating forms of carbon, such as diamond or buckyballs (carbon-60), the ratio of magnetization to applied field – the “diamagnetic susceptibility” – is very small. However, the susceptibility of conducting forms of carbon, such as graphite and some carbon nanotubes, is two orders of magnitude greater and second only to that of superconductors.
This large diamagnetism occurs because graphite is a semi-metal, which means its valence and conduction bands overlap by a tiny amount. The number of electrons and holes in small overlapping regions is only about 10-5 per carbon atom, compared with one conduction electron per atom in copper. We need to apply a magnetic field to the samples to see if they are magnetic, but for perpendicular applied fields the susceptibility of graphite sheets is so high that the diamagnetic signal completely swamps the ferromagnetic signal. The situation is even worse for conducting nanotubes. As a result, small ferromagnetic moments are most easily detected in the insulating forms of carbon, or in graphite with the magnetic field applied in the plane of the sheets.
Firm evidence
In 2003 Pablo Esquinazi and co-workers at the University of Leipzig in Germany found evidence for magnetic order in a series of graphite samples in the presence of a parallel magnetic field. The magnetization ranged in strength from 0.3-2.5 × 10-3 A m2 kg-1, and in half of their samples the magnetization was greater than could possibly be accounted for by iron impurities. But the magnetization varied from one sample to the next, which meant that is was unlikely that the ferromagnetism was an intrinsic property of the carbon.
However, it was an experiment performed two years earlier with carbon-60 that proved to be the catalyst for the current interest in magnetic carbon. Tatiana Makarova of the Ioffe Physico-Technical Institute in St Petersburg, Russia, and co-workers, including Esquinazi, found a small ferromagnetic signal in a form of carbon-60 that had a rhombohedral structure. Although the samples showed a magnetization of just 10-3 A m2 kg-1, the result suggested that pure carbon could somehow be ferromagnetic.
But where did the magnetism come from? The Curie temperature of 500 K did not correspond to that of any obvious impurity, and the magnetism appeared only in a narrow range of temperatures and pressures. Indeed, the team was not even looking for signs of magnetism in carbon but for superconductivity.
Then in 2002 one of us (MC) and co-workers at Trinity College Dublin thought of checking graphite-rich fragments from the Canyon Diablo meteorite, which crashed into the Arizona desert 50,000 years ago. We found that only about two-thirds of the magnetization – which has an average value of 20 A m2 kg-1 – in this remarkable source of extraterrestrial carbon could be accounted for by the magnetic minerals present. This meant that the rest of the magnetization was somehow associated with the carbon content of the meteorite, which had presumably existed for billions of years before experiencing the shock of the impact (see Physics World December 2002 p3).
Earlier this year, John Giapintzakis of the University of Crete and colleagues found evidence for ferromagnetism in an ultra-low-density carbon “foam”, which was prepared by blasting a high-power laser onto an extremely pure carbon target. Using electron microscopy, Giapintzakis and co-workers observed that the material consists of randomly interconnected carbon clusters with average diameters of between 6-9 nm. The “nanofoam” had a Curie temperature of 90 K and a magnetic moment of about 0.4 A m2 kg-1 at room temperature, although this disappeared within a few hours of the foam being produced (see Physics World May p3).
The suspects
One of the most likely explanations for magnetic ordering in carbon is that it is caused by some kind of defect structure. Following the m–J paradigm, researchers have therefore been trying to find out whether defects in carbon can sustain a magnetic moment, m, and whether these moments order magnetically due to some form of exchange coupling, J. If this is the case, it should be possible to start with a nonmagnetic specimen and then make it magnetic by appropriate irradiation.
In 2003 Esquinazi’s group in Leipzig did just that by irradiating spots on a sheet of highly oriented graphite with protons and alpha particles. The researchers found that irradiation with protons led to a measurable magnetic moment but alpha particles did not. Signs of magnetism also appeared in the proton-irradiated spots when they were scanned with a magnetic force microscope. Defects in irradiated graphite have also been a topic of interest in nuclear technology, because they are produced in large quantities in the graphite moderators of nuclear reactors. It seems as if some of the defects in the moderator material can trap two electrons and form a triplet state.
There are three possible defect “suspects” that might be involved in the magnetic order in graphite (figure 3). Suspect 1 is the adatom, a carbon atom that lies on a graphene plane and that, in its stable configuration, occupies a bridge-like position in the middle of a carbon-carbon bond. Two of its four valence electrons participate in covalent bonds with the graphene carbon atoms: one goes to a “dangling” sp2 orbital that forms no bond, and the other is shared between this dangling orbital and the remaining p orbital. This last orbital lies parallel to the graphene surface, where it does not form any bond but possesses a magnetic moment of about 0.5 Bohr magnetons (μB). In terms of the atomic magnetization, 1 μB per carbon atom is equivalent to a magnetization of 465 A m2 kg-1.

Suspect 2 is a carbon vacancy, which is obtained by removing an atom from the graphene sheet. Two of the three carbon atoms adjust their bonds to accommodate the vacancy and the remaining atom moves slightly out of the graphene plane. A singly occupied, dangling sp2 orbital is left, which generates a magnetic moment of about 1 μB. Earlier this year, Sumio Iijima of the National Institute for Advanced Industrial Science and Technology in Tsukuba, Japan, and co-workers visualized both adatoms and carbon vacancies with a transmission electron microscope.
The third suspect – zigzag edges in graphitic ribbons that have “flat” energy bands – has been around for 10 years, but it has generated a lot of excitement recently. This is because flat bands are known to split such that the “spin-up” band becomes lower in energy than the “spin-down” band, causing the material to become ferromagnetic.
The study of these edge states has been stimulated by a theorem developed decades ago by Elliott Lieb, now at Princeton University. This theorem states that the ground state of a lattice, such as a graphene sheet, that divides into two sublattices is magnetic. For this to happen, electrons must only be able to hop from lattice A to lattice B and vice versa, but without direct A-A or B-B hopping. The total spin is then ½ (NA–NB), where NA and NB are the number of sites on the two sublattices.
If the edge states in a graphitic ribbon with only two bonds are terminated in different ways, for example with one hydrogen atom on one edge and two hydrogen atoms on the other, then NA≠NB and the ribbon possesses a magnetic moment (see figure 3). Calculations of electronic structure have confirmed that such high-spin graphitic fragments do exist, although, interestingly, both the band formation and the magnetic ground state appear to be rather sensitive to the stacking of the graphene planes. However, there is no direct experimental evidence for these magnetic edges so far.
Indeed, there has been little progress in the search for a motive for any of these suspects to couple together to create a ferromagnetic state in carbon, since there is no obvious reason for strong exchange interactions to take place between the defects. In other words, the J part of the m–J paradigm is missing. One may speculate that the magnetic defects are coupled over long distances by indirect exchange with some conduction electrons, as happens in diluted magnetic semiconductors. However, the conduction electrons in graphite form a quasi 2D electron gas, giving a Curie temperature of about 1 K, so such a mechanism can hardly be responsible for room-temperature magnetism. The same argument applies to magnetic transition-metal impurities in graphite: they may have a high spin state but their magnetic coupling is likely to be very weak.
Clearly, the theoretical search for the suspects and motive for ferromagnetism in graphite-based systems is in its infancy. Perhaps one should consider more complex defects beyond the “usual suspects”. Or perhaps we need a completely new mechanism that goes beyond the m–J paradigm, such as a Bose-Einstein condensation of molecular triplet states.
Contact-induced magnetism
There is another way in which conducting carbon could become magnetic: by contact with a ferromagnetic metal. Whenever two metals touch, electrons flow between them in order to equalize their chemical potentials. If one of the metals is a ferromagnet with different densities of spin-up and spin-down electrons, this charge transfer is accompanied by a net transfer of spin. (The extreme case is a half-metal that contains conducting electrons with only one spin, which means that the charge transfer is completely spin polarized.) This contact-induced magnetism should always be present at interfaces, and it has been proposed as an explanation for the magnetization of graphite in the Canyon Diablo meteorite.

This year, contact-induced magnetism was demonstrated independently by two groups. In the first, Oscar Céspedes and the present authors in Dublin placed a carbon nanotube on a smooth film of a ferromagnetic metal. Provided the magnetization is uniform, the film produces no stray field (figure 4). However, if spin-polarized electrons are transferred to the nanotube, it looks like a tiny bar magnet and creates a stray field in its vicinity. The stray field was detected by the force exerted on the vibrating magnetic tip of a magnetic force microscope, which revealed that the nanotube had a magnetization of 0.5 A m2 kg-1.
In the other experiment, Hans-Christoph Mertins of the University of Applied Sciences in Munster, Germany, and co-workers produced a material made from alternating layers of iron and carbon layers with thicknesses of 2.55 and 0.55 nm. Then, by measuring the absorption of polarized electromagnetic radiation, they showed that the carbon had a magnetic moment of approximately 20 A m2 kg-1.
The crucial point in both these experiments is that no magnetism is found unless a ferromagnetic material is present (carbon nanotubes on copper or silicon substrates, for example, do not show any magnetic moment). However, a successful explanation for magnetic carbon in terms of contact-induced magnetism needs more than just the presence of high-spin impurities in carbon. We also need evidence for a ferromagnetic second phase, such as iron dispersed in tiny drops throughout the carbon.
Magnetic prospects
As we have shown, there are various pieces of evidence that suggest carbon can be magnetically ordered. But what about the other elements in the third island of stability in the magnetic periodic table? Do they exhibit high-temperature ferromagnetism too?
Some two-electron defect centres in oxides have long been known to have a spin triplet as a low-lying excited state. Recently, our group found that thin films of hafnium oxide and calcium boride are ferromagnetic, although neither compound contains magnetic ions or is magnetic in bulk form. Furthermore, the magnetization of these films does not increase with thickness beyond a few nanometres, and the moment is a few 100 μB per square nanometre of substrate area.
The origin of this magnetism seems to lie in defects in the film near the interface with the substrate. The problem, as with carbon, is less finding magnetic defect centres than finding a reason why they should order magnetically at such high temperatures.There may be a novel explanation.A clue may be provided by the hafnium-oxide films, which have a remarkable anisotropy in their magnetization that suggests there is a large orbital contribution to the magnetic moment.
Unlike the spin magnetic moment, the magnetic moments associated with the electron orbital motion are usually destroyed in solids. The prospect of ordered orbital magnetic moments is therefore an exciting one.
The possibility of creating magnetic carbon in a systematic and controllable way is a tantalizing prospect. Based on currently reported values of magnetization, however, it seems unlikely that the magnetism of carbon will ever bestrong enough to make it useful as a bulk magnetic material. A magnetization of 1 Am2 kg-1 is some two orders of magnitude lower than that of the materials used in high-performance magnets.
The prospects for spin-electronics are brighter, since carbon could, in principle, provide the way to integrate spin and molecular electronics. The weak spin-orbit and hyperfine interactions in carbon promote long diffusion lengths and coherence times, and therefore offer ideal conditions for coherent spin manipulation. In addition, the contact-induced magnetic effect paves the way for devices where the magnetic contacts used for the spin manipulation can be decoupled from the current/voltage probes. The carbon era of spinelectronics may be dawning.



