The internet appears to have taken on a life of its own ever since the National Science Foundation in the US gave up stewardship of the network in 1995. New lines and routers are added continually by thousands of companies, none of which require permission from anybody to do so, and none of which are obliged to report their activity. This uncontrolled and decentralized growth has turned network designers into scientific explorers. All previous Internet-related research concentrated on designing better protocols and faster components. More recently, an increasing number of scientists have begun to ask an unexpected question: what exactly did we create?

One thing is clear. While entirely of human design, the emerging network appears to have more in common with a cell or an ecological system than with a Swiss watch. Many diverse components, each performing a specialized job, contribute to a system that is evolving and changing at an incredible speed. Increasingly, we are realizing that our lack of understanding of the Internet and the Web is not a computer-science question. Rather it is rooted in the absence of a scientific framework to characterize the topology of the network behind it.

Networks and graphs have long been studied in a prolific branch of mathematics known as graph theory. Until recently, the absence of detailed topological information about large complex systems, such as communication networks or cells, meant that networks were modelled as “random graphs”. The most widely investigated random-graph model was introduced by Hungarian mathematicians, Paul Erdös and Alfred Rényi, in 1960. Their influential model consists of N nodes, each of which has a probability, p, of being connected to another node via a link (figure 1a).

For such a random network the probability that a node has k links follows a Poisson distribution, implying that it is exponentially rare to find a node with a high number of links. But the Erdös-Rényi model raises an important question: do we believe that networks observed in nature are truly random? Could the Internet really offer us the relatively fast and seamless service we currently enjoy if the computers were connected randomly to each other? Or, to take a more extreme example: would you be able to read this article if the chemicals in your body decided to react randomly to each other, bypassing the rigid chemical web that they normally obey?

Intuitively the answer is no – we all feel that behind every complex system there is an underlying network with non-random topology. The challenge for physicists is to unearth the signatures of order from the apparent chaos of millions of nodes and links. Following this path, in the last few years we have learned that the tools of statistical mechanics are particularly well suited to this task, offering an unexpected perspective on the structure and dynamics of many truly complex interacting systems, including the Internet and its offshoot the World Wide Web.

Complex networks

According to a recent study by Steve Lawrence of the NEC Research Institute in New Jersey and Lee Giles of Pennsylvania State University, the Web contains nearly a billion documents. The documents represent the nodes of this complex network and they are connected by locators, known as URLs, that allow us to navigate from one Web page to another.

To analyse the Web’s properties, we need to draw a map that tells us how the pages link to each other. This information is routinely collected by search engines, such as Google and AltaVista. But the companies that have developed these engines are often reluctant to share the information for research purposes. Thus we needed to obtain a map of our own. This is exactly what the current author together with Réka Albert and Hawoong Jeong, also at the University of Notre Dame, did in 1998. We wrote a robot or Web crawler that started from a given Web page, collected all the outgoing links, and followed these links to visit more pages and collect even more links. Through this iterative process we mapped out a tiny fraction of the Web, amounting to less than 0.05% of its total size.

As the Web is a “directed” network, each document can be characterized by the number of incoming, k_in, and outgoing, k_out, links. The first quantities that we investigated were the probability distributions, P(k), that a randomly selected Web page has exactly k_in or k_out links, respectively. Guided by random-graph theory, we expected that P(k) would follow a binomial distribution and would converge to a Poisson distribution when the number of nodes was large. So it was rather surprising when our data indicated that P(k) decayed via a power law – a completely different type of distribution (figures 1c and d). Indeed, we found that the probability was given by k ^{– G}, where G = 2.45 for outgoing links and G = 2.1 for incoming links, a result that was confirmed in a parallel study by Ravi Kumar and co-workers at IBM’s Almaden Research Center in California.

There are major topological differences between networks with Poisson and power-law distributions. For random networks, most nodes have approximately the same number of links, k ~ <k>, where k> represents the average value. The exponential decay of P(k) guarantees the absence of nodes with significantly more than <k> links. In contrast, the power-law distribution implies that there is an abundance of nodes with only a few links, and a small – but significant – minority that have a very large number of links.

A road map that has cities as nodes and motorways as links is a good example of an exponential network because most cities are located at the intersection of motorways. In contrast, networks that can be described by a power-law distribution look more like the airline route maps found in glossy in-flight magazines. Although most airports are served by a small number of carriers, there are a few hubs, such as Chicago or Frankfurt, from which links emerge to almost all other US or European airports, respectively. Just like the smaller airports, the majority of documents on the Web have only a few links (figures 1e and f).

Since a typical node in an exponential network has k ~ <k> links, the average number of links is an important characteristic. However, <k> is not a particularly significant quantity in a power-law distribution. This absence of an intrinsic scale in k prompted us to call networks with a power-law degree distribution “scale free”. The finding that the Web is a scale-free network raised an important question: would such inhomogenous topology also emerge in other complex systems?

Recently an answer to this question came from an unexpected direction – the Internet itself. The Internet forms a physical network, the nodes of which are “routers” that navigate packets of data from one computer to another, and groups of routers and computers that are called “domains”. The links that join the nodes together are the various physical connectors, such as phone wires and optical cables (figure 2). Due to the physical nature of the connections, this network was expected to be different from the Web, where adding a link to an arbitrary remote page is as easy as linking to a computer in the next room.

To the surprise of many, the network behind the Internet also appears to follow a power-law distribution. This result was first noticed by three brothers, Michalis Faloutsos of the University of California at Riverside, Petros Faloutsos of the University of Toronto and Christos Faloutsos of Carnegie Mellon University. When they analysed the Internet at the router and domain level, they found that the degree distribution follows a power law with an exponent of G = 2.5 for the router network and G = 2.2 for the domain map. This indicates that the wiring of the Internet is also dominated by several highly connected hubs.

Separated by 19 clicks

In 1967 Stanley Milgram, a sociologist at Harvard University in the US, surprised the world with a bold claim: any person in the world can be traced to any other by a chain of five or six acquaintances. That is, despite the six billion inhabitants of our planet, we live in a “small world”. This feature of social networks came to be known as “six degrees of separation” after John Guare’s Broadway play and movie. In addition, sociologists have repeatedly argued that nodes (i.e. people) in social networks are grouped in small clusters, representing circles of friends and acquaintances in which each node is connected to all other nodes, with only a few weak links to the world outside their own circle of friends.

While the existence of such local clustering and small-world behaviour agrees with our intuition, these features were not expected to be relevant beyond social systems. It came as a surprise, therefore, when Duncan Watts of Columbia University and Steven Strogatz of Cornell University found that many networks in nature, such as the brain of the worm C. elegans, as well as the network of movie actors in Hollywood and the network of power lines in western America, simultaneously have a small node separation and display a high degree of clustering. The question is whether the Internet and the Web follow this paradigm?

For a proper answer we need a full map of the Web. But, as Lawrence and Giles have shown, even the largest search engines cover only 16% of the Web. This is where the tools of statistical mechanics come in handy – they can be used to infer the properties of the complete network from a finite sample. To achieve this our group at Notre Dame constructed small models of the Web on a computer, making sure that the distribution of links matched the functional form that we had previously measured.

Next we identified the shortest distance between two nodes, defined as the number of clicks required to get from one page to another, and averaged over all pairs of nodes to obtain the average node separation, d. Repeating this process for networks of different sizes using a technique called “finite size scaling” – a standard procedure in statistical mechanics – we inferred that the average node separation is given by d = 0.35 + 2.06 log(N), where N is the number of nodes. This expression predicts typically that the shortest path between two pages selected at random among the 800 million nodes (i.e. documents) that made up the Web in 1999 is around 19 – assuming that such a path exists. This path, however, is not guaranteed because the Web is a directed network, i.e. a link from one page to another does not imply the existence of an inverse link. Consequently, not all pairs of nodes can be connected – a feature factored into the calculation that leads to the expression for d.

An extensive study by a collaboration between IBM, Compaq and AltaVista has subsequently found that the shortest distance between any two nodes in a sample of 200 million is 16. This value is in good agreement with our prediction of 17 for a sample of this size.

These results clearly indicated that the Web represents a small world, i.e. the typical number of clicks between two Web pages is about 19, despite the fact that there are now over one billion pages out there. And as Lada Adamic of Stanford University in the US has shown, the Web also displays a high degree of clustering. The probability that two neighbours of a given node are linked together is much greater than the value expected for a random network without clustering. Results from our group indicate that the Internet follows suit – the typical separation between two routers is nine. In other words, a packet of data can reach any router within 10 hops, and the network is highly clustered, demonstrating that the small-world paradigm has rapidly infiltrated the Earth’s newly developing electronic skin as well.

Evolving networks

Why do systems as different as the Internet, which is a physical network, and the Web, which is virtual, develop similar scale-free networks? We have recently traced the emergence of the power-law distribution back to two common mechanisms that are absent from the classical-graph models, but are present in many complex networks.

First, traditional graph-theory models assume that the number of nodes in a network is fixed. In contrast, the Web continually expands by the addition of new pages, while the Internet grows by the installation of new routers and communication links. Second, while random-graph models assume that the links are distributed randomly, most real networks exhibit a phenomenon called “preferential attachment”, i.e. they contain nodes that have a high probability of being connected to another node with a large number of links. For example, we are far more likely to link our Web page to the most popular documents on the Web, as these are the ones we know about. Meanwhile, network engineers tend to connect their company or institution to the Internet through points that have a high bandwidth, which inevitably implies a high number of other consumers, or links.

Based on these two ingredients, we constructed a simple model in which a new node was added to the network at every time step, linking it to some of the nodes already present in the system (figure 1b). The probability, Pi(k), that a new node connects to a node with k links follows preferential attachment, i.e. Pi(k) = k/Sigma_ik_i, where the denominator is summed over all nodes.

Numerical simulations indicate that the resulting network is indeed scale-free, and the probability that a node has k links follows a power law with an exponent of G = 3. This simple model illustrates how growth and preferential attachment jointly lead to the appearance of a hierarchy. A node rich in links increases its connectivity faster than the rest of the nodes because incoming nodes link to it with higher probability – this “rich-gets-richer” phenomenon is present in many competitive systems.

Traditionally networks were viewed as static objects with a constant number of nodes. In contrast, scale-free models view networks as dynamical systems that self-assemble and evolve in time through the addition and removal of nodes and links. Such a dynamical approach follows the long tradition of physics-based modelling, aiming to capture what nature did when it assembled these networks. The expectation behind these modelling efforts is that if we capture the microscopic processes that drive the placement of links and nodes, then the structural elements and the topology will follow. In addition, viewing evolving networks as dynamical systems allows us to predict many of their properties analytically. For example, in the scale-free model the rate at which a node acquires new links is given by dk/dt = mPi(k), where m is the number of links that a new node has when it joins the network. This expression predicts that each node increases its connectivity over time according to the power law k(t) = t^ß, where ß = 1/2 is the dynamic exponent.

The scale-free model is the simplest example of an evolving network. In real systems, however, the probability Pi(k) that a new node connects to one with k links can be nonlinear. As Paul Krapivsky and Sid Redner of Boston University have shown, such nonlinearities result in deviations from power-law behaviour. Moreover, links are often added to real networks between existing nodes, or nodes and links can disappear. Indeed, Jose Mendes of the University of Porto in Portugal and colleagues, plus several other groups, have demonstrated that the presence of such events can modify the exponent, G, allowing for practically any value between one and infinity. In addition, Luis Amaral and collaborators at Boston University have shown that aging and saturation effects limit the number of links that a node can acquire, thereby inducing exponential cut-offs in P(k).

Power laws regularly greet us in critical phenomena and describe, for example, the freezing of water or the ordering of spins in a magnet. But there is a crucial difference between these systems and evolving networks. In critical phenomena the exponents are fixed and universal, i.e. they cannot be tuned easily by modifying some parameters in the system. In networks, however, the exponent G can be changed continuously by changing almost every parameter that governs the link and nodes. Thus universality as we know it is absent. However, most complex systems share the same dynamical character as evolving networks, indicating that their topology and evolution cannot be divorced from each other.

Bose-Einstein condensation

In most complex systems, the nodes vary in their ability to compete for links. Some Web pages, for instance, quickly acquire a large number of links through a mixture of good content and marketing. A good example is the Google search engine, which in less than two years has become one of the most connected nodes of the Web.

This competition for links can be incorporated into the scale-free model by adding a “fitness”, eta_i, to each node, i, to describe its ability to compete for links at the expense of other nodes. A Web page with good up-to-date content and a friendly interface, for example, has a greater fitness than a low-quality page that is only updated occasionally. The probability Pi(k_i) that a new node connects to one with k_i links is then modified such that Pi(k_i) = eta_i k_i/Sigma_j eta_j k_j.

The competition generated by the various fitness levels means that each node evolves differently in time compared with others. Indeed, the connectivity of each node is now given by k_i(t) ~= t^ß(eta), where the exponent ß(eta) increases with eta. As a result, fit nodes (ones with large eta) can join the network at some later time and connect to many more links than less-fit nodes that have been around for longer.

Amazingly, such competitive-fitness models appear to have close ties with Bose-Einstein condensation, currently one of the most investigated problems in atomic physics. In an atomic gas, the atoms are distributed among many different energy levels. In a Bose-Einstein condensate, however, all the particles accumulate in the lowest energy ground state of the system and are described by the same quantum wavefunction.

By replacing each node in the network with an energy level having energy epsilon_i= exp(-ß eta_i), Ginestra Bianconi and I found that the fitness model maps exactly onto a Bose gas (figure 3). According to this mapping, the nodes map to energy levels while the links are represented by atoms in these levels.

The behaviour of a Bose gas is uniquely determined by the distribution g(epsilon) from which the random energy levels (or fitnesses) are selected. One expects that the functional form of g(epsilon) depends on the system. For example, the attractiveness of a router to a network engineer comes from a rather different distribution than the fitness of a dot.com company competing for customers.

For a wide class of g(epsilon) distributions, a “fit-get-richer” phenomena emerges. Although the fittest node acquires more links than its less-fit counterparts, there is no clear winner. On the other hand, certain g(epsilon) distributions can result in Bose-Einstein condensation, where the fittest node does emerge as a clear winner. It develops a condensate by acquiring a significant fraction of the links, independent of the size of the system. In network language this corresponds to a “winner-takes-all” phenomenon. While the precise form of the fitness distribution for the Web or the Internet is not known yet, it is likely that g(epsilon) could be measured in the near future. Eventually we may be able to answer the intriguing question: could the Web or the Internet represent a gigantic Bose condensate?

The Achilles’ heel of the Internet

As the world economy becomes increasingly dependent on the Internet, a much-voiced concern arises. Can we maintain the functionality of the network under the inevitable failures or frequent attacks by computer hackers? The good news is that so far the Internet has proven rather resilient against failures: while about 3% of the routers are down at any moment, we rarely observe major disruptions. Where does this robustness come from? While there is a significant error tolerance built into the protocols that govern the switching of data packets, we are beginning to learn that the scale-free topology also plays a crucial role.

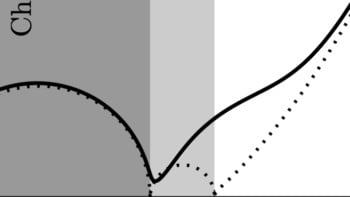
In trying to understand the topological component of error tolerance, we can get help from a field of physics known as percolation. Percolation theory tells us that if we randomly remove nodes, then at some critical fraction, f_c, the network should fragment into tiny, non-communicating islands of nodes. To our considerable surprise, simulations on scale-free networks do not support this prediction. Even when we remove up to 80% of the nodes, the remainder still form a compact cluster (figure 4).

The mystery was resolved last year by Reuven Cohen of Bar-Ilan University in Israel and co-workers. They showed that as long as the connectivity exponent G is less than three (which is the case for most real networks, including the Internet) the critical threshold for fragmentation is f_c = 1. This is a wonderful demonstration that scale-free networks cannot be broken into pieces by the random removal of nodes, a result also supported by the independent calculations of Duncan Callaway and collaborators at Cornell University.

This extreme robustness to failures is rooted in the inhomogeneous topology of the network. The random removal of nodes is most likely to affect small nodes rather than hubs with many links because nodes significantly outnumber hubs. Therefore the removal of a node does not create a significant disruption in the network topology, just like the closure of a small local airport has little impact on international air traffic. The bad news is that the inhomogeneous topology has its drawbacks as well. Scale-free networks are rather vulnerable to attacks. Indeed, the absence of a tiny fraction of the most-connected nodes will cause the network to break into pieces.

These findings uncovered the underlying topological vulnerability of scale-free networks. While the Internet is not expected to break under the random failure of the routers and lines, well informed hackers can easily design a scenario to handicap the network.

Computer viruses that disable local computers and programmes are another threat in the on-line world. Recently Romualdo Pastor-Satorras from Universitat Politecnica de Catalunya in Barcelona, Spain, and Allessandro Vespigniani from the International Centre for Theoretical Physics in Trieste, Italy, demonstrated that viruses behave rather differently on scale-free networks compared with random networks.

For decades, both marketing experts and epidemiologists have intensively studied so-called diffusion theories. These theories predict a critical threshold for virus spreading. Viruses that are less contagious than a well defined threshold will inevitably die out, while those that are above the threshold will multiply exponentially and eventually reach the whole system. The Barcelona-Trieste group, on the other hand, has found that the threshold for a scale-free network is zero. In other words, all viruses, even those that are only weakly contagious, will spread and persist in the system. This explains why “Love Bug”, the most damaging virus so far, is still the seventh most frequent virus, a year after its introduction and supposed eradication.

Our improved understanding of real networks might provide new insights into the spread of ideas and biological viruses among the human population, networks that appear to be as inhomogenous as scale-free networks. It also suggests that we should take another look at the volumes of research written on the interplay of network topology, fads and epidemics.

The original creators of the Internet could not have foreseen the exploding demand for bandwidth and the emergence of new technologies. These changes will require new communication protocols that can respond to this high and sophisticated demand. Moreover, any change in the current protocols requires extensive testing and optimization, which is very sensitive to the underlying network topology.

The recent realization that all models based on the random-network topology are simply inappropriate to describe real systems sparked a race among computer scientists to create new generators with a more realistic topology. An equally high-stakes race is on to develop better search engines by capitalizing on the emerging understanding of the Web’s large-scale topology. In this respect, Google appears to be winning – it became the most popular search engine by ranking documents based on the topological position of the nodes within the network, cleverly exploiting the Web’s inhomogenous architecture.

But the implications of network research resonate well beyond computer science. Scale-free networks appear to be the architecture of choice for nature when it comes to complex systems. By working together with Zoltán Oltvai, a cell biologist from Northwestern University in the US, we have recently found that the metabolic and the protein-protein interaction networks of cells follow a scale-free topology in all investigated organisms. Moreover, Ricard Sole and collaborators at Barcelona have shown that some food webs that depict how species interact with each other are best described as scale-free networks. And it appears that the phenomenal robustness of these networks plays a key role in both of these systems. The network’s inhomogeneity contributes to the well known resilience of cells against random mutations and explains why ecosystems do not collapse under the random disappearance of species.

The advances discussed here represent only the tip of the iceberg. Networks represent the architecture of complexity. But to fully understand complex systems, we need to move beyond this architecture and uncover the laws that govern the underlying dynamical processes, such as Internet traffic or reaction kinetics in cells.

Most importantly, we need to understand how these two layers of complexity – architecture and dynamics – evolve together. These are all formidable challenges for physicists, biologists and mathematicians alike, inaugurating a new era that Stephen Hawking recently called the century of complexity.