There is much to learn when it comes to applying the tools of physics to conception, pregnancy and babyhood, as Michael Banks explains

Becoming a parent or carer for the first time is a joyous, if fairly loud, occasion. When a baby enters the world covered in bodily fluids, they inflate their lungs to take a breath and let out an ear-piercing cry. It’s the first sign for bleary-eyed expectant parents that their life will never quite be the same – they will soon get to grips with constant feeds, dirty nappies and, of course, a lack of sleep. Part of the challenge for new parents is dealing with the many changes that lie ahead, not only in their own life but that of the newborn; as babies rapidly develop in the coming days, months and years.
“The first thousand days” is a common term used by paediatricians to describe the period from conception to the child’s second birthday – a time during which so many critical developments occur; right from the very moment of conception as the embryo, and then fetus, undergo rapid daily transformations. Some nine months later at birth, the infant’s reliance on the placenta to sustain itself in utero comes to an end. The baby must get to grips with breathing on its own and feeding on the breast or from the bottle while also adapting to their new environment. Months later, the development takes on other dimensions as the infant rolls, crawls, stands on unsteady legs, and then ultimately walks. If that wasn’t enough, there is also the not-so-small matter of communication, by learning a language.
Given how crucial the first thousand days are; many aspects concerning conception, pregnancy and babyhood remain woefully understudied
It is easy to take any of these individual milestones for granted – and many parents do, for no fault of their own. After all, infants are seemingly built to take on these challenges. But considering how crucial these two-and-a-half years are, many aspects concerning conception, pregnancy and babyhood remain woefully understudied. Pregnancy, for example, has commonly been seen as something to be endured rather than investigated. Research on the properties and working of the placenta, uterus and cervix, lags decades behind that of other organs such as the heart, lungs and brain. One reason for this is the ethical perspective of studying pregnant women and newborn babies; not to mention the fact that research into healthcare for women has long been marginalized, and often overlooks key differences between men and women. Studies must be carefully designed, and various ethical procedures and guidelines need to be adhered too. That will remain; but what is different today is finally seeing these topics as worthy of investigation in the first place – a move that has also been helped by advances in imaging and theoretical techniques.
While some may think that it is only biology and neuroscience that can shine a light on conception, pregnancy and babyhood, physics too has the necessary tools to provide a fresh perspective into many of these issues. Physics plays a key role in everything from how sperm are able to navigate the complex fluids of the female reproductive system to reach the egg (see “Conception – life begins at low Reynolds number”); to the forces that are involved to support the development of the embryo; and how the placenta is able to control the diffusion of a wide range of solutes to and from the fetus (see “Pregnancy and the placenta; the tree of life”). Physical processes are involved in the manner that contractions can coordinate and travel across the uterus to expel a baby; how a newborn can effortlessly extract milk from the breast; what acoustic properties of babies’ cries make them so hard to ignore; and how toddlers are able to learn grammar so effectively (see “Babyhood – it’s good to talk”).
Today, research into these matters from a physical-science perspective is not only throwing up surprises about what the human body is capable of, but is also highlighting potential treatments – from new methods to monitor fetal movements, to innovative ways to help premature babies to breath. Such endeavours are also deepening our appreciation of the processes that life has put in place to propagate itself. And there remains much more to discover.
Conception – life begins at low Reynolds number
“[Sperm] is an animalcule which mostly…swims with its head or front part in my direction. The tail, which, when swimming, it lashes like a snakelike movement, like eels in water.” So wrote the Dutch businessman and scientist Antonie van Leeuwenhoek to the Royal Society in the 1670s concerning his observations of sperm. Using his custom-built microscopes, which were more powerful than anything made before, van Leeuwenhoek was the first to peer into the microscopic realm. His devices, which were about the size of a hand, let him image objects with micrometre resolution, clearly resolving many different types of “animalcule” that reside on or in the body, including sperm.
Despite van Leeuwenhoek’s acute observations, it took hundreds of years to get any firm idea about how sperm could propel through the complex fluids that exist within the female reproductive tract. The first clues came in the late 1880s from the Irish physicist Osborne Reynolds who worked at Owens College in England (now the University of Manchester). During that time, Reynolds conducted a series of fluid-dynamics experiments, and from them obtained a relationship between the inertia that a body in a liquid can provide and the viscosity of the medium – the Reynold’s number. Roughly speaking, a large object in a liquid such as water would have a large Reynolds number, which means inertial forces created by the object are dominant. But for a microscopic body, such as sperm, it would be the viscous forces of the liquid that would have the most influence.
The physics explaining this strange world where viscous forces dominate was worked out by several physicists in the 1950s, including Geoffrey Taylor from the University of Cambridge. Conducting experiments using glycerine, a high-viscosity medium, he showed that at a low Reynolds number, the physics of a swimming microorganism could be explained by “oblique motion”. If you take a thin cylinder, such as a straw, and let it fall upright in a high-viscosity fluid like syrup, it will do so vertically – as you may expect. If you put the straw on its side, it will still drop vertically, but half as fast as the upright case due to increased drag. However, when you put the straw diagonally and let it fall, it does not move vertically downwards but falls in a diagonal direction – what is known as oblique motion.
This occurs because the drag along the length of the body is lower than in the perpendicular direction – meaning that the straw wants to move along its length faster than it does perpendicular, so it slips horizontally as well as falling vertically. In the early 1950s, Taylor and Geoff Hancock from the University of Manchester, UK, carried out detailed calculations about how a sperm could travel. They showed that as the sperm whips its tail, it creates oblique movements at different sections, producing viscous propulsion.
Today, researchers are building ever complex models for how sperm swim. These models are not just for theoretical insights, but also have applications in assisted reproduction techniques. Mathematician David Smith from the University of Birmingham, UK – who has worked on biological fluid dynamics for over two decades – and colleagues have developed a sperm-analysis technique. Dubbed Flagella Analysis and Sperm Tracking (FAST), it can image and analyse the tail of a sperm in exquisite detail. From the images, it uses mathematical models to calculate how much force the body is applying to the fluid. The package also calculates the sperm’s swimming efficiency – how far it moves using a certain amount of energy.
The team began clinical trials with FAST in 2018, and if the technique is successful, it could help couples assess what type of assisted reproduction technique may work for them. The simulations may show, for example, that “intrauterine insemination” – in which sperm are washed and then injected into the uterus, bypassing the cervical canal – could be just as successful over several cycles as carrying out more expensive and invasive IVF procedures. Alternatively, their technique could be used to help to analyse the impact of male contraception. “This project is about harnessing 21st-century technologies to address male fertility problems,” says Smith.
Pregnancy and the placenta – the tree of life
Consisting of a network of thick purple vessels and resembling a flat cake, the placenta is the life-giving alien within. An organ unique to pregnancy, a healthy placenta at full term is around 22 centimetres in diameter, 2.5 centimetres thick, and with a mass of about 0.6 kg. It is a direct link between the mother and fetus, providing the fetus with oxygen and nutrients, and allowing it to send back waste products, such as carbon dioxide and urea, a major component of urine.
From just a collection of cells in early pregnancy, the placenta begins to form a basic structure once it intertwines with the lining of the uterus. This eventually leads to a network of fetal vessels that branch out to form villous trees – a bit like Japanese bonsais – that are bathed in maternal blood in the “intervillous space”. The placenta could be described as fifty connected bonsai trees upside down at the top of a fish tank that is full of blood, thanks to the pumping of several maternal arteries at the bottom.

Estimated to contain around 550 km of fetal blood vessels – similar in length to the Grand Canyon – the placenta’s total surface area for gas exchange is around 13 m2. Part of the difficulty studying the placenta is due to these varying scales. The other issue is knowing how this huge network of fetal vessels, which are each about 200 μm across, ultimately affects the performance of a centimetre-scale organ.
The exchange of gases between maternal and fetal blood is via diffusion through the villous tree tissue – with the fetal vessels closest to the villous tissue thought to be doing the exchange. By combining experimental data with mathematical modelling of the intricate geometry of the fetal blood vessels, for the past decade mathematician Igor Chernyavsky from the University of Manchester and colleagues have been studying the transport of gases and other nutrients in the placenta.
The team found that despite the incredibly complex topology of the fetal vessels, there is a key dimensionless number that can explain the transport of different nutrients in the placenta. Determining the chemical state of a mixture is a complex problem – the only “reference” state being equilibrium, when all the reactions balance each other and end up in a stable composition.
In the 1920s, physical chemist Gerhard Damköhler attempted to work out a relationship for the rate of chemical reactions or diffusion in the presence of a flow. In this non-equilibrium scenario, he came up with a single number – the Damköhler number – that can be used to compare the time for the “chemistry to happen” with the flow rate in the same region.
The Damköhler number is useful when it comes to the placenta because the organ is diffusing solutes – such as oxygen, glucose and urea – in the presence of both a fetal and maternal blood flow. Here, the Damköhler number is defined as the ratio between the amount of diffusion against the rate of blood flow. For a Damköhler number larger than one, diffusion dominates and occurs faster than the blood flow rate, known as “flow limited”. For a number less than one, the flow rate is greater than the diffusion rate, known as “diffusion limited”. Chernyavsky and colleagues found that, despite the various complex arrangements of fetal capillaries in the terminal villus, the movement of different gases in and out of the fetal capillaries could be described by the Damköhler number – which he called the “unifying principle” in the placenta.
The researchers found, for example, that carbon monoxide and glucose in the placenta are diffusion limited, while carbon dioxide and urea are more flow limited. Carbon monoxide is thought to be efficiently exchanged by the placenta, which is why maternal smoking and air pollution can be dangerous for the baby. Intriguingly, oxygen is close to being both flow and diffusion limited, suggesting a design that is perhaps optimized for the gas; which makes sense given it is so critical to life.
It is unknown why there is such a wide range of Damköhler numbers, but one possible explanation is that the placenta must be robust, given its many different roles, which include both nourishing and protecting the baby from harm. Given the difficulty of experimentally studying the placenta both in utero and when it is delivered in the third stage of labour, there is still a lot we don’t know about this ethereal organ.
Babyhood – it’s good to talk

It is difficult to express how hard, in principle, it is for infants to pick up their language – but they seem remarkably good at doing so. When a child is two to three years old, its language becomes sophisticated incredibly quickly, with toddlers being able to construct complex – and grammatically correct – sentences. This development is so rapid that it is difficult to study, and is far from being fully understood. Indeed, how infants learn language is hotly contested, with many competing theories among linguists.
Almost all human languages can be described with what is known as a context-free grammar – a set of (recursive) rules that generates a tree-like structure. The three main aspects of a context-free grammar are “non-terminal” symbols, “terminal” symbols, and “production rules”. In a language, non-terminal symbols are aspects like noun phrases or verb phrases (i.e. parts of the sentence that can be broken down into smaller parts). Terminal symbols are produced when all the operations have been carried out, such as the individual words themselves. Finally, there are the hidden production rules that determine where the terminal symbols should be placed, to produce a sentence that makes sense.
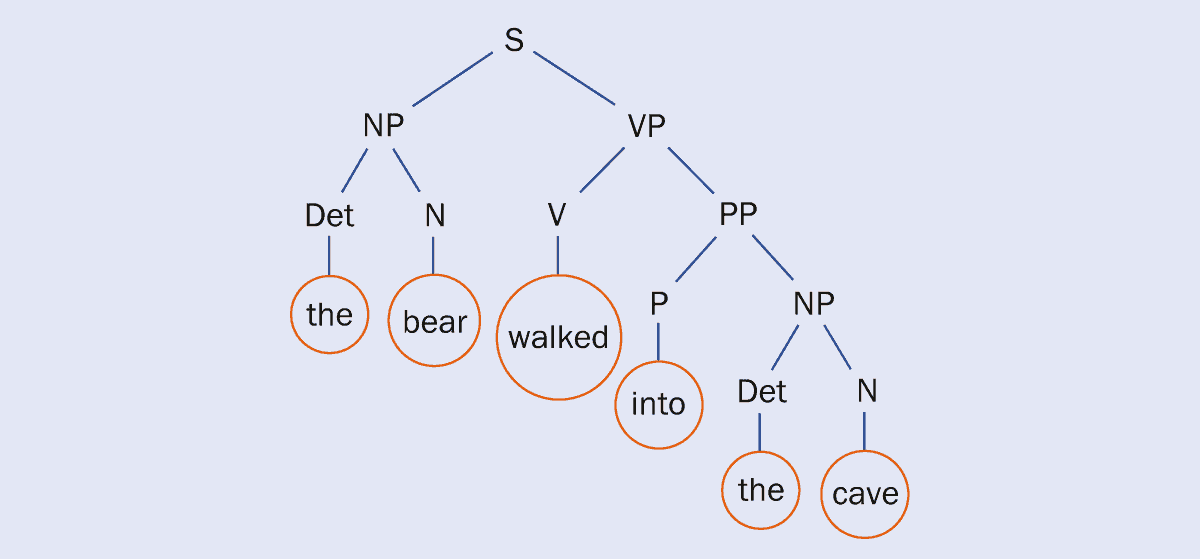
A sentence in a context-free grammar language can be visualized as a tree, with the branches being the “non-terminal” objects that the infant does not hear when learning language – such as verb phrases, and so on. The leaves of the tree, meanwhile, are the terminal symbols, or the actual words that are heard. For example, in the sentence “The bear walked into the cave”, “the bear” and “walked into the cave” can be split off to form a noun phrase (NP) and a verb phrase (VP), respectively. Those two parts can then be split further until the final result is individual words including determiners (Det) and prepositional phrases (PP) (see figure). When infants listen to people talking in fully formed sentences (that are, hopefully, grammatically correct), they are only exposed to the leaves of the tree-like network (the words and location in a sentence). But somehow, they also have to extract the rules of the language from the mixture of words they are hearing.
In 2019, Eric De Giuli from Ryerson University in Canada modelled this tree-like structure using the tools of statistical physics (Phys. Rev. Letts. 122 128301). As infants listen, they continually adjust the weights of the branches of possibilities as they hear language. Eventually, branches that produce nonsensical sentences acquire smaller weights – because they are never heard – as compared to information-rich branches that are given larger weights. By continuously performing this ritual of listening, the infant “prunes” the tree over time to discard random-word arrangements, while retaining those with meaningful structure. This pruning process reduces both the number of branches near the tree’s surface and those deeper down.
The fascinating aspect of this idea from a physical point of view is that when the weights are equal, language is random – which can be compared to how heat affects particles in thermodynamics. But once weights are added to the branches and adjusted to produce specific grammatical sentences, the “temperature” begins to decrease. De Giuli ran his model for 25,000 possible distinct “languages” (which included computer languages), and found universal behaviour when it came to “decreasing the temperature”. At a certain point, there is a sharp drop in what is analogous to thermodynamic entropy, or disorder, when the language goes from a body of random arrangements to one that has high-information content. Think of a bubbling pot of jumbled words that is taken off the stove to cool, until words and phrases begin to “crystallize” into a specific structure or grammar.
This abrupt switch is also akin to a phase transition in statistical mechanics – at a certain point, the language switches from a random jumble of words to a highly structured communication system that is rich in information, containing sentences with complex structures and meanings. De Giuli thinks that this model (which he stresses is only a model and not a definitive conclusion for how infants learn language) could explain why at a certain stage of development a child learns incredibly quickly to construct grammatical sentences. There comes a point when they have listened to enough for it all to make sense to them. Language, it seems, is just child’s play.
- The Secret Science of Baby: the Surprising Physics of Creating a Human, from Conception to Birth – and Beyond by Michael Banks was published by BenBella Books in December 2022



