Materials known as topological insulators have the unusual property of being able to conduct electricity on their surface even though they are insulators inside. If that weren’t strange enough, physicists have now shown experimentally that such materials can exist in four spatial dimensions. The researchers, based in Singapore and the UK, achieved this feat by wiring up a stack of electric circuit boards to represent a highly interconnected lattice, and say that their scheme could be extended to five or even six dimensions.
The importance of topology can be seen by comparing the spatial characteristics of a sphere and a doughnut. It’s not possible to transform one into the other by gradually varying their shapes – no amount of stretching, squeezing or other distortion will turn a doughnut into a sphere, and vice-versa. Such a change can only come about through an abrupt, discontinuous action – the insertion or removal of a hole.
A similar idea underpins topological insulators, but the transformation in this case doesn’t involve a material’s spatial properties. Instead, it concerns the wavefunctions of the electrons flowing in the material. These contain what is in effect a knot, making it impossible to smoothly convert a topological insulator into a normal insulator. Instead, the material must first become a metal. This means that the material’s physical boundary with the outside world conducts electricity, even though its bulk is insulating.
This phenomenon has previously been seen in two and three dimensions. In the former case, first observed in 2007 and similar to the quantum Hall effect, the material in question consists of an insulating plane with one-dimensional electric currents flowing around the edge. The latter case, detected from 2008 onwards, sees currents flowing in a range of directions across the surfaces of a bulk insulator. In both cases, the currents are generated when an electron’s spin interacts with its orbital motion as it travels through space. These currents persist even when the edges or surfaces involved are deformed.
Beyond three dimensions
Theorists tell us that topological insulators should also exist in higher dimensions. Indeed, researchers have previously observed them in four dimensions, but they did so by mapping a 4D system to a 2D one. The latest work instead involves the direct creation of a 4D topological insulator that acts as a standard insulator when confined to three or fewer dimensions, and only exhibits its exotic properties once it is extended into the fourth.
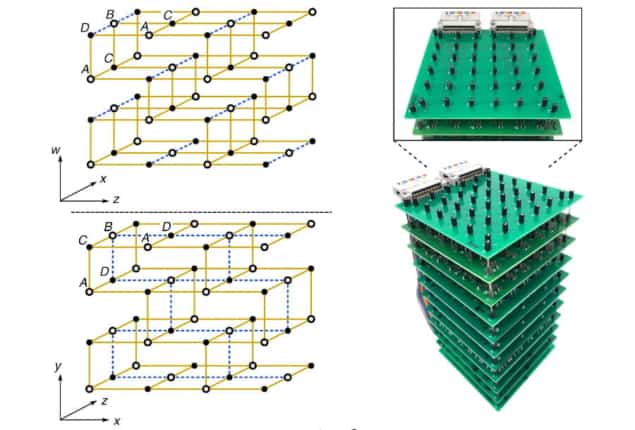
The new 4D insulator is based on a model drawn up by Hannah Price of the University of Birmingham, and has been experimentally realized by a team led by Yidong Chong at Nanyang Technological University. To create their insulator, the team relied on an artificial construct known as a metamaterial. Building this metamaterial involved making dozens of electrical oscillators from capacitors and inductors, and then arranging them in grids on several circuit boards stacked on top of one another. With each oscillator behaving like an artificial atom, says Chong, the system as a whole acts like a crystal through which electric current can flow.
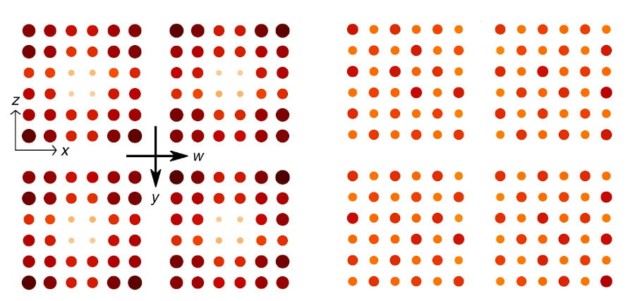
The idea was to hook up the oscillators so that they behave electrically as they would in four dimensions, even though they are actually sitting in our 3D world. As Chong explains, this wouldn’t be possible if each oscillator were only linked to its nearest neighbours. But an extra dimension can be added to an otherwise one-dimensional row of oscillators by linking each of those objects to two others further up and down the line. This idea can then be extrapolated so that in 3D space connections beyond those to the (six) nearest neighbours yield a circuit that behaves as if it were sitting in 4D-space.
Testing predictions
To test their system, Chong and colleagues sent voltage pulses through the circuits. They found that when the circuits were wired up according to Price’s model those pulses propagated in waves across the connections made to create the material’s 3D “surface” but not within the 4D bulk. They also observed that by tweaking the circuit components they could make the waves disappear from the surface – so turning the material into a straightforward insulator.
According to Chong, scientists had previously thought it impossible to realize such a 4D system experimentally. “It was believed to be just the province of theoretical study,” he says. “The trick here is that we are not using an actual material but a synthetic one.”
Krzysztof Sacha of Jagiellonian University in Poland, who was not involved in the research, reckons that the work bodes well for possible applications of topological insulators, given that the surface states remained intact even though the components had imprecise values of capacitance and inductance. “Such robustness of topological systems to perturbation is very promising from the point of view of future applications where quantum computing is one of the most important candidates,” he says.

What is a topological insulator?
Price says that this particular research won’t be applied to quantum computers because the metamaterial used is a purely classical system that can’t support entanglement. But she argues that the work paves the way for other higher-dimensional systems. “There are suggestions that some really cool things could happen in 5D and 6D,” she says.
Chris Hooley of the University of St Andrews in the UK also thinks it unlikely that this particular system will have immediate applications. But he agrees that in the long term, technology could benefit. “The general idea that protected surface states might be of use in quantum computation has been around for a while,” he notes. “And this sort of system gives us some new kinds of protected surface state, so one never knows!”
The research is published in Nature Communications.