Fraudsters routinely try to make money by pretending they have been injured in traffic accidents. But as Michael Hall explains, simple Newtonian physics can reveal which claims are genuine and which are bogus
It’s a clear sunny day and a bus is driving down the road. It comes to a halt at a bus stop and a group of men get on board. As the driver moves off, he notices a car pull up behind the bus, but it avoids obvious opportunities to overtake. Suddenly, the car accelerates and crashes into the rear of the bus. CCTV recordings show the group that boarded clutch their necks, looking around in apparent surprise. Two of them even throw themselves on the floor of the bus.
The collision is hardly registered by other passengers, some of whom appear bemused by the antics of the men. In fact, data recorders fitted to the bus show it to be travelling at barely 25 km/h when the incident occurs. The bus company’s insurers receive a number of claims for injury, loss of earnings and lifestyle impact. But on viewing the video evidence, the insurers are not convinced by the claims.
While the video recordings indicate a fraud, they alone may not be enough to persuade a judge in a civil court. The insurers therefore instruct GBB – the firm I work for – to investigate. Our job is to use a science-based analysis that will form part of a wider accident investigator’s forensic report. Our analysis has to be impartial and watertight so that it will stand up to the scrutiny of cross examination.
Fortunately, we have information from the bus’s on-board event data recorder, in the form of a graph of the bus’s acceleration versus time. Simple Newtonian physics indicates that the bus would have changed speed by no more than 1.5 km/h during the collision. Even with an uncertainty of 20%, that’s well below the threshold for injury and, in our opinion, the men were unlikely to have been hurt. As for the car, its mass was one-eighth of the bus so its speed would have changed by about 12 km/h, which was consistent with the damage to it.
What a scam!
The case was quite rightly thrown out, but fake claims like this one are a big problem. According to the UK’s Insurance Fraud Bureau, there were 2.7 million motor-insurance claims in Britain between October 2019 and the end of 2020. More than 6% – roughly 170,000 – were linked to suspected “crash for cash” scams. Many were created by a relatively small number of companies or gangs, with plenty avoiding court prosecution entirely.
Physics and cars: an evolving journey
In these incidents, drivers seek to defraud insurers by deliberately and premeditatively manufacturing a car crash, often involving an innocent party in another vehicle. The fraudsters try to limit the magnitude of the crash – usually by driving at relatively low speeds – so that none of the perpetrators get injured. In general, though, they don’t care what happens to the innocent parties in the other vehicle.
The resulting damage to the vehicles is genuine (even if some may have been caused by earlier incidents) but the claimants will be lying when they say they got hurt. Criminals – often working in cahoots with third parties – can make tens of thousands of pounds by claiming for injury, repair bills (that are often exaggerated) and storage costs. There’s another kind of scam too, in which drivers who have been involved in a genuine and un-premeditated low-speed collision file a claim for a fictitious injury just because “everyone is doing it”.

The police aren’t usually called out to either type of incident as they generally don’t involve serious personal injury or major damage to property (walls, houses, lamp posts and so on). In fact, most claims are quickly settled by insurers, who don’t have the resources to check out every claim. However, the resulting cost of these fake claims – including medical costs, car repairs, replacement hire cars and so on – runs into hundreds of millions of pounds in the UK alone.
That’s why a small proportion of cases do get investigated, especially if the circumstances surrounding the accident are not clear, if a claim appears exaggerated or if there are suspicions of fraud. (Another example is shown in figure 1.) Collision investigators will inspect the damage to vehicles – either in person or from photos – and try to answer the following questions.
- Did the vehicles actually collide?
- Is the accident geometry described by the claimant or defendant consistent with the damage to both vehicles?
- Is there damage, such as paint transfer, that provides a forensic link between the vehicles?
- Is there other damage that may have been caused in another unrelated incident?
- What might the repair costs be?
- How likely is it that the occupants of the claimant’s vehicle were thrown about in the car such that whiplash or other soft-tissue injuries occurred?
The trouble is that whiplash and similar physical injuries are easy to fake because there are no diagnostic tools, such as X-ray scans, that can unequivocally confirm that such an injury has occurred. Experience has shown that a clear and concise “science” section in an accident investigator’s report can carry a lot of weight with judges who are deciding if a claim is fake or genuine. In addition to calculations based on Newton’s laws, the report may also include details of crash tests and possibly even a computer simulation of the collision.
A crash-course in crash physics
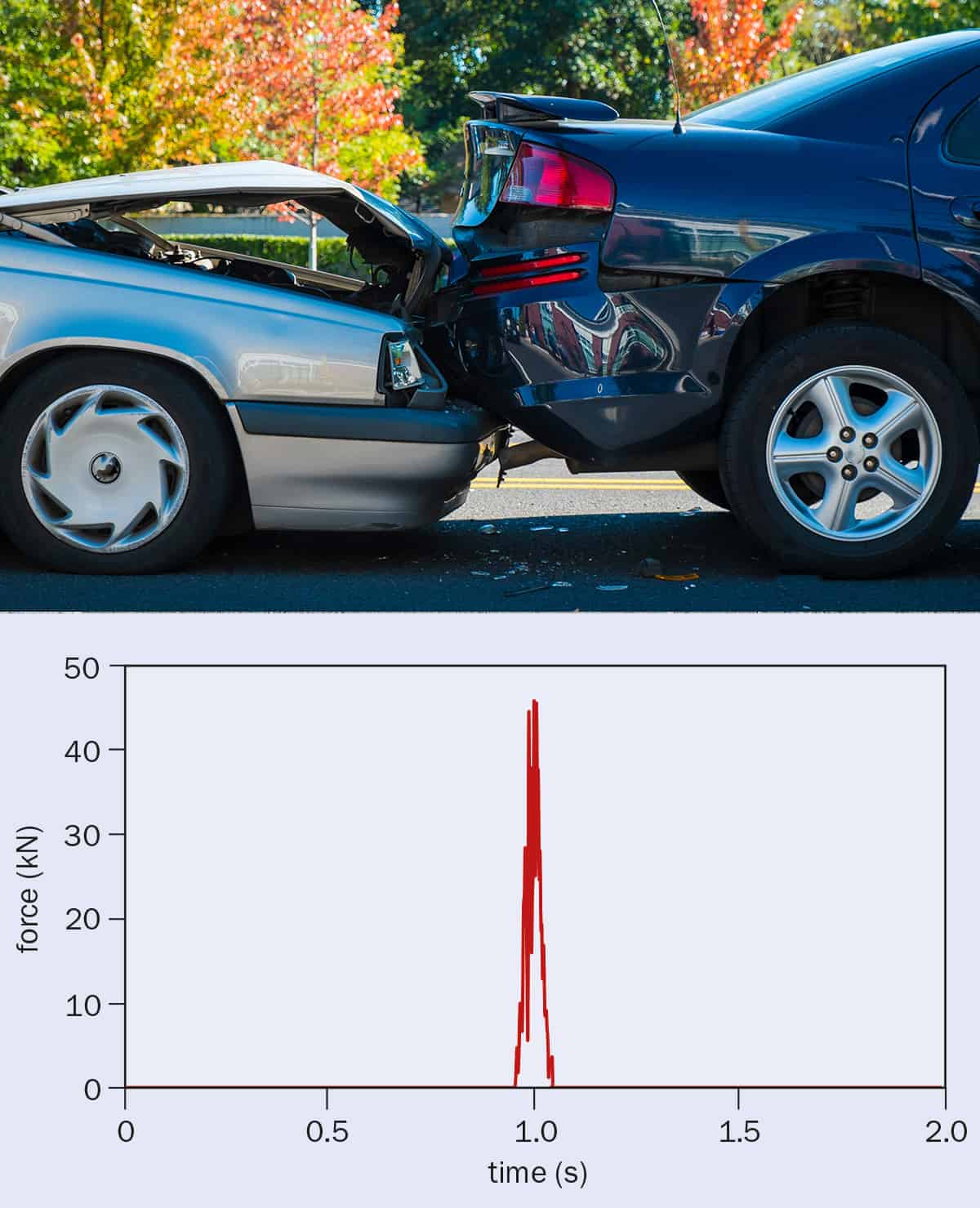
Collisions between objects are a staple of school-physics syllabuses, but there is more to the subject than meets the eye. You’ll know that when two vehicles collide, a force acts between them for the time they are in contact, typically about 0.1 s. However, the force is not uniform. Measurements made using accelerometers fitted to vehicles in experimental crash tests reveal a ragged pulse that peaks about half-way through the crash (figure 2).
As Newton’s second and third laws of motion dictate, the struck or “target” vehicle will experience a positive version of this pulse (causing it to accelerate), while the striking or “bullet” vehicle will experience a negative version of this pulse (causing it to decelerate).
During the collision itself, the two vehicles will become entangled and briefly form a composite system. The vehicles will initially squish together, before expanding as they spring elastically apart and then, finally, separating.
However, no two collisions are ever exactly the same. One or both drivers might slam on their brakes. The struck vehicle might have been stationary and had its hand brake on. The bullet vehicle might have been at rest and the other driver reversed into it. One common scam is for the driver of a vehicle in slow-moving traffic to brake hard and hope that the vehicle behind will run into their rear. Quite often, the scammer’s car will have its brake lights disconnected to confuse the driver behind and make a crash more likely.
One scam is for the driver of a vehicle to brake hard and hope that the vehicle behind will run into their rear.
If a car is about to hit your car from behind – and you can’t avoid the impact – there are two things you can do. If you want to minimize damage to your cherished car, don’t brake. Not braking will lead to a lower collision force, making the impact slightly more elastic and leading to less damage to your prized possession. (Remember, though, that if there’s another vehicle in front, you may be shunted into its rear, leading to a three-body collision and a separate insurance claim and all the headaches that involves.)
On the other hand, if you want to minimize the risk of injuring yourself and any fellow passengers, slam on the brakes as hard as you can. That might seem counter-intuitive because the collision force will be greater. However, it will be opposed by the braking force, which will reduce the acceleration of anyone in your car and thus the potential for, say, whiplash. Let’s hope, though, that the driver behind isn’t a crook out to cause a crash: in an ideal world, they would put on their brakes too.
The importance of e
For collision investigators, Newtonian mechanics provides a series of handy equations covering quantities such as average collision force (with or without braking), the change in speed of the target vehicle and the kinetic energy dissipated, which dictates how much the vehicles will be damaged. These equations will require the mass of each vehicle, the relative impact speed (V), the coefficient of restitution (e), the collision time period (Δt) and any braking coefficients.
Defined as the ratio of the relative speed of two vehicles before and after a collision, e is also a measure of the elasticity of the crash. It can range from 1 for a perfectly elastic crash (impossible for a real crash) to 0 for an entirely inelastic smash-up (where the vehicles stick together and don’t spring apart). The value of e is crucial because it dictates the overall speed change of the target vehicle, which in turn influences how likely an occupant struck at low speeds (15 km/h or less) is to suffer from whiplash or other soft-tissue symptoms.
The reason why collision investigators use speed change – rather than acceleration or force – as a metric for assessing injury symptoms is that its value can be accurately determined. There is, in contrast, a much bigger uncertainty over the acceleration during a car crash as it depends on Δt, for which we do not have an accurate figure. Knowing the speed changes also lets us determine what happens to the kinetic energy of the car as it crashes (figure 3).

But how do we know the speed change in a particular crash? Collision investigators do this by turning to test crashes carried out under controlled conditions, which contain quantitative data as well as photos of the smashed-up vehicles. We look for examples where similar damage was caused to the case in question, from which we can estimate how fast the vehicles were moving before they collided. Mathematical correlations between Δt (which varies little with impact speed) and e (which depends a lot on impact speed) are used to refine the estimate of e, from which the speed change can be derived.
Another way of estimating the speed change is to look up the kinetic energy dissipated during a similar test crash. Using Newtonian physics, we can use this energy to calculate the impact speed assuming our collision was entirely inelastic (i.e. e = 0). In reality, e will not be exactly 0 so we obtain a more accurate value of it by iterating our calculations until the impact speed converges to within about 1 km/h. With our better value of e, we can then easily calculate the speed change.
A collision investigator who has a reasonable value for the coefficient of restitution, e, can judge the merits of a low-speed claim.
The bottom line is that a collision investigator who has a reasonable value for e can judge the merits of a low-speed claim. Unfortunately, vehicle collisions are nonlinear events, in which small changes in the initial conditions (such as speed, contact height and the angle at which the cars strike each other) result in large changes in e and Δt. No two crash tests will ever be exactly the same and there is large scatter in the value of both parameters, leading to uncertainties of as much as 30% in the calculated value of the collision force (in fact the equations are much more sensitive to uncertainties in Δt than in e).
Claims and counter-claims
To see what this means in practice, my firm was once asked to study a crash in which car A (1370 kg) ran into the back of car B (1645 kg) waiting at traffic lights. The driver of B claimed he sustained a whiplash injury, while A stated he had “barely touched” car B. Our firm inspected the damage to car B, which matched damage visible on photos of A’s car. We then compared the damage with crash test data from similar vehicles, indicating the total damage to both vehicles would have required a dissipation of 3 ± 1 kJ of kinetic energy.

How to hack a self-driving car
Using Newtonian mechanics, we calculated that the effective mass of the colliding vehicles was 747 kg, while the impact speed (assuming a perfectly elastic collision) would have been 10.8 km/h. Using crash-test data, we assumed the collision lasted 0.12 s, leading to a collision force of ± 25.0 kN. From this, Newton’s second law yielded an acceleration of 15.2 m/s2, with the resulting speed change 5.6–7.4 km/h.
For car A, that speed change is below the threshold for a soft-tissue injury. Indeed, any braking would have reduced these speed changes still further. So in the opinion of the GBB investigator, as expressed in the forensic report, any unusual occupant movement was unlikely. On this basis, B’s claim for injury was dismissed and the insurance company avoided being defrauded.
Be a better driver
Ultimately, you may be involved in a crash through no fault of your own and your best bet is to try to avoid collisions in the first place by driving within the speed limit, slowing down when wet and keeping a good distance from the car in front. But if you are involved in a crash, remember that what happens will be dictated by a simple application of Newton’s laws of motion. A competent collision investigator with sufficient knowledge of maths and physics will be able to comment on the validity of any claim. So if your case ends up before a judge, you can be sure that you have science on your side.




