My involvement with high-temperature superconductors began in the autumn of 1986, when a student in my final-year course on condensed-matter physics at the University of Birmingham asked me what I thought about press reports concerning a new superconductor. According to the reports, two scientists working in Zurich, Switzerland – J Georg Bednorz and K Alex Müller – had discovered a material with a transition temperature, Tc, of 35 K – 50% higher than the previous highest value of 23 K, which had been achieved more than a decade earlier in Nb3Ge.
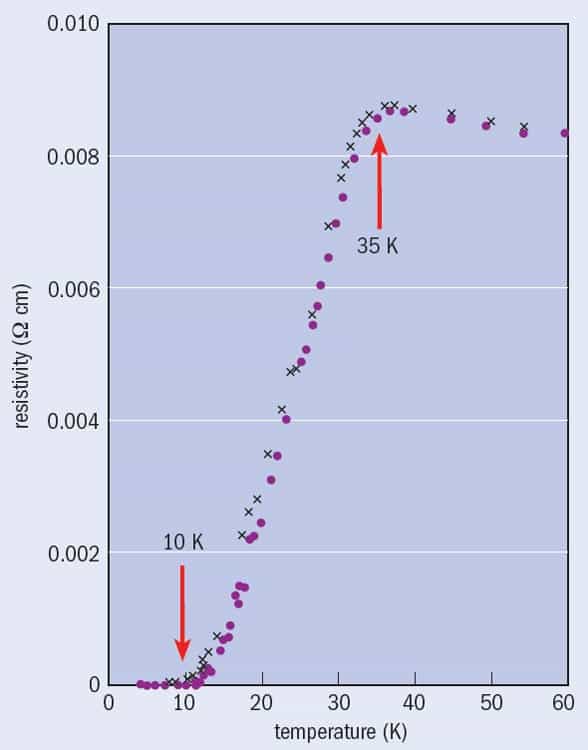
In those days, following this up required a walk to the university library to borrow a paper copy of the appropriate issue of the journal Zeitschrift für Physik B. I reported back to the students that I was not convinced by the data, since the lowest resistivity that Bednorz and Müller (referred to hereafter as "B&M") had observed might just be comparable with that of copper, rather than zero. In any case, the material only achieved zero resistivity at ~10 K, even though the drop began at the much higher temperature of 35 K (figure 1).
In addition, the authors had not, at the time they submitted the paper in April 1986, established the composition or crystal structure of the compound they believed to be superconducting. All they knew was that their sample was a mixture of different phases containing barium (Ba), lanthanum (La), copper (Cu) and oxygen (O). They also lacked the equipment to test whether the sample expelled a magnetic field, which is a more fundamental property of superconductors than zero resistance, and is termed the Meissner effect. No wonder B&M had carefully titled their paper "Possible high Tc superconductivity in the Ba–La–Cu–O system" (my italics).
My doubt, and that of many physicists, was caused by two things. One was a prediction made in 1968 by the well-respected theorist Bill McMillan, who proposed that there was a natural upper limit to the possible Tc for superconductivity – and that we were probably close to it. The other was the publication in 1969 of Superconductivity, a two-volume compendium of articles by all the leading experts in the field. As one of them remarked, this book would represent "the last nail in the coffin of superconductivity", and so it seemed: many people left the subject after that, feeling that everything important had already been done in the 58 years since its discovery.
In defying this conventional wisdom, B&M based their approach on the conviction that superconductivity in conducting oxides had been insufficiently exploited. They hypothesized that such materials might harbour a stronger electron–lattice interaction, which would raise the Tc according to the theory of superconductivity put forward by John Bardeen, Leon Cooper and Robert Schrieffer (BCS) in 1957 (see "The BCS theory of superconductivity" below). For two years B&M worked without success on oxides that contained nickel and other elements. Then they turned to oxides containing copper – cuprates – and the results were as the Zeitschrift für Physik B paper indicated: a tantalizing drop in resistivity.
What soon followed was a worldwide rush to build on B&M's discovery. As materials with still higher Tc were found, people began to feel that the sky was the limit. Physicists found a new respect for oxide chemists as every conceivable technique was used first to measure the properties of these new compounds, and then to seek applications for them. The result was a blizzard of papers. Yet even after an effort measured in many tens of thousands of working years, practical applications remain technically demanding, we still do not properly understand high-Tc materials and the mechanism of their superconductivity remains controversial.
The ball starts rolling
Although I was initially sceptical, others were more accepting of B&M's results. By late 1986 Paul Chu's group at the University of Houston, US, and Shoji Tanaka's group at Tokyo University in Japan had confirmed high-Tc superconductivity in their own Ba–La–Cu–O samples, and B&M had observed the Meissner effect. Things began to move fast: Chu found that by subjecting samples to about 10,000 atmospheres of pressure, he could boost the Tc up to ~50 K, so he also tried "chemical pressure" – replacing the La with the smaller ion yttrium (Y). In early 1987 he and his collaborators discovered superconductivity in a mixed-phase Y–Ba–Cu–O sample at an unprecedented 93 K – well above the psychological barrier of 77 K, the boiling point of liquid nitrogen. The publication of this result at the beginning of March 1987 was preceded by press announcements, and suddenly a bandwagon was rolling: no longer did superconductivity need liquid helium at 4.2 K or liquid hydrogen at 20 K, but instead could be achieved with a coolant that costs less than half the price of milk.
Chu's new superconducting compound had a rather different structure and composition than the one that B&M had discovered, and the race was on to understand it. Several laboratories in the US, the Netherlands, China and Japan established almost simultaneously that it had the chemical formula YBa2Cu3O7–d, where the subscript 7–d indicates a varying content of oxygen. Very soon afterwards, its exact crystal structure was determined, and physicists rapidly learned the word "perovskite" to describe it (see "The amazing perovskite family" below). They also adopted two widely used abbreviations, YBCO and 123 (a reference to the ratios of Y, Ba and Cu atoms) for its unwieldy chemical formula.
The competition was intense. When the Dutch researchers learned from a press announcement that Chu's new material was green, they deduced that the new element he had introduced was yttrium, which can give rise to an insulating green impurity with the chemical formula Y2BaCuO5. They managed to isolate the pure 123 material, which is black in colour, and the European journal Physica got their results into print first. However, a group from Bell Labs was the first to submit a paper, which was published soon afterwards in the US journal Physical Review Letters. This race illustrates an important point: although scientists may high-mindedly and correctly state that their aim and delight is to discover the workings of nature, the desire to be first is often a very strong additional motivation. This is not necessarily for self-advancement, but for the buzz of feeling (perhaps incorrectly in this case) "I'm the only person in the world who knows this!".
"The Woodstock of physics"
For high-Tc superconductivity, the buzz reached fever pitch at the American Physical Society's annual "March Meeting", which in 1987 was held in New York. The week of the March Meeting features about 30 gruelling parallel sessions from dawn till after dusk, where a great many condensed-matter physicists present their latest results, fill postdoc positions, gossip and network. The programme is normally fixed months in advance, but an exception had to be made that year and a "post-deadline" session was rapidly organized for the Wednesday evening in the ballroom of the Hilton Hotel. This space was designed to hold 1100 people, but in the event it was packed with nearly twice that number, and many others observed the proceedings on video monitors outside.
Müller and four other leading researchers gave talks greeted with huge enthusiasm, followed by more than 50 five-minute contributions, going on into the small hours. This meeting gained the full attention of the press and was dubbed "the Woodstock of physics" in recognition of the euphoria it generated – an echo of the famous rock concert held in upstate New York in 1969. The fact that so many research groups were able to produce results in such a short time indicated that the B&M and Chu discoveries were "democratic", meaning that anyone with access to a small furnace (or even a pottery kiln) and a reasonable understanding of solid-state chemistry could confirm them.
With so many people contributing, the number of papers on superconductivity shot up to nearly 10,000 in 1987 alone. Much information was transmitted informally: it was not unusual to see a scientific paper with "New York Times, 16 February 1987" among the references cited. The B&M paper that began it all has been cited more than 8000 times and is among the top 10 most cited papers of the last 30 years. It is noteworthy that nearly 10% of these citations include misprints, which may be because of the widespread circulation of faxed photocopies of faxes. One particular misprint, an incorrect page number, occurs more than 250 times, continuing to the present century. We can trace this particular "mutant" back to its source: a very early and much-cited paper by a prominent high-Tc theorist. Many authors have clearly copied some of their citations from the list at the end of this paper, rather than going back to the originals. There have also been numerous sightings of "unidentified superconducting objects" (USOs), or claims of extremely high transition temperatures that could not be reproduced. One suspects that some of these may have arisen when a voltage lead became badly connected as a sample was cooled; of course, this would cause the voltage measured across a current-carrying sample to drop to zero.
Meanwhile, back in Birmingham, Chu's paper was enough to persuade us that high-Tc superconductivity was real. Within the next few weeks, we made our own superconducting sample at the second attempt, and then hurried to measure the flux quantum – the basic unit of magnetic field that can thread a superconducting ring. According to the BCS theory of superconductivity, this flux quantum should have the value h/2e, with the factor 2 representing the pairing of conduction electrons in the superconductor. This was indeed the value we found (figure 2). We were amused that the accompanying picture of our apparatus on the front cover of Nature included the piece of Blu-Tack we used to hold parts of it together – and pleased that when B&M were awarded the 1987 Nobel Prize for Physics (the shortest gap ever between discovery and award), our results were reproduced in Müller's Nobel lecture.
Unfinished business
In retrospect, however, our h/2e measurement may have made a negative contribution to the subject, since it could be taken to imply that high-Tc superconductivity is "conventional" (i.e. explained by standard BCS theory), which it certainly is not. Although B&M's choice of compounds was influenced by BCS theory, most (but not all) theorists today would say that the interaction that led them to pick La–Ba–Cu–O is not the dominant mechanism in high-Tc superconductivity. Some of the evidence supporting this conclusion came from several important experiments performed in around 1993, which together showed that the paired superconducting electrons have l = 2 units of relative angular momentum. The resulting wavefunction has a four-leaf-clover shape, like one of the d-electron states in an atom, so the pairing is said to be "d-wave". In such l = 2 pairs, "centrifugal force" tends to keep the constituent electrons apart, so this state is favoured if there is a short-distance repulsion between them (which is certainly the case in cuprates). This kind of pairing is also favoured by an anisotropic interaction expected at larger distances, which can take advantage of the clover-leaf wavefunction. In contrast, the original "s-wave" or l = 0 pairing described in BCS theory would be expected if there is a short-range isotropic attraction arising from the electron–lattice interaction.
These considerations strongly indicate that the electron–lattice interaction (which in any case appears to be too weak) is not the cause of the high Tc. As for the actual cause, opinion tends towards some form of magnetic attraction playing a role, but agreement on the precise mechanism has proved elusive. This is mainly because the drop in electron energy on entering the superconducting state is less than 0.1% of the total energy (which is about 1 eV), making it extremely difficult to isolate this change.
On the experimental side, the maximum Tc has been obstinately stuck at about halfway to room temperature since the early 1990s. There have, however, been a number of interesting technical developments. One is the discovery of superconductivity at 39 K in magnesium diboride (MgB2), which was made by Jun Akimitsu in 2001. This compound had been available from chemical suppliers for many years, and it is interesting to speculate how history would have been different if its superconductivity had been discovered earlier. It is now thought that MgB2 is the last of the BCS superconductors, and no attempts to modify it to increase the Tc further have been successful. Despite possible applications of this material, it seems to represent a dead end.
In the same period, other interesting families of superconductors have also been discovered, including the organics and the alkali-metal-doped buckyball series. None, however, have raised as much excitement as the development in 2008 (by Hideo Hosono's group at Tokyo University) of an iron-based superconductor with Tc above 40 K. Like the cuprate superconductors before them, these materials also have layered structures, typically with iron atoms sandwiched between arsenic layers, and have to be doped to remove antiferromagnetism. However, the electrons in these materials are less strongly interacting than they are in the cuprates, and because of this, theorists believe that they will be an easier nut to crack. A widely accepted model posits that the electron pairing mainly results from a repulsive interaction between two different groups of carriers, rather than attraction between carriers within a group. Even though the Tc in these "iron pnictide" superconductors has so far only reached about 55 K, the discovery of these materials is a most interesting development because it indicates that we have not yet scraped the bottom of the barrel for new mechanisms and materials for superconductivity, and that research on high-Tc superconductors is still a developing field.
A frictionless future?
So what are the prospects for room-temperature superconductivity? One important thing to remember is that even supposing we discover a material with Tc ~ 300 K, it would still not be possible to make snooker tables with levitating frictionless balls, never mind the levitating boulders in the film Avatar. Probably 500 K would be needed, because we observe and expect that as Tc gets higher, the electron pairs become smaller. This means that thermal fluctuations become more important, because they occur in a smaller volume and can more easily lead to a loss of the phase coherence essential to superconductivity. This effect, particularly in high magnetic fields, is already important in current high-Tc materials and has led to a huge improvement in our understanding of how lines of magnetic flux "freeze" in position or "melt" and move, which they usually do near to Tc, and give rise to resistive dissipation.
Another limitation, at least for the cuprates, is the difficulty of passing large supercurrents from one crystal to the next in a polycrystalline material. This partly arises from the fact that in such materials, the supercurrents only flow well in the copper-oxide planes. In addition, the coupling between the d-wave pairs in two adjacent crystals is very weak unless the crystals are closely aligned so that the lobes of their wavefunctions overlap. Furthermore, the pairs are small, so that even the narrow boundaries between crystal grains present a barrier to their progress. None of these problems arise in low-Tc materials, which have relatively large isotropic pairs.
For high-Tc materials, the solution, developed in recent years, is to form a multilayered flexible tape in which one layer is an essentially continuous single crystal of 123 (figure 3). Such tapes are, however, expensive because of the multiple hi-tech processes involved and because, unsurprisingly, ceramic oxides cannot be wound around sharp corners. It seems that even in existing high-Tc materials, nature gave with one hand, but took away with the other, by making the materials extremely difficult to use in practical applications.
Nevertheless, some high-Tc applications do exist or are close to market. Superconducting power line "demonstrators" are undergoing tests in the US and Russia, and new cables have also been developed that can carry lossless AC currents of 2000 A at 77 K. Such cables also have much higher current densities than conventional materials when they are used at 4.2 K in high-field magnets. Superconducting pick-up coils already improve the performance of MRI scanners, and superconducting filters are finding applications in mobile-phone base stations and radio astronomy.
In addition to the applications, there are several other positive things that have arisen from the discovery of high-Tc superconductivity, including huge developments in techniques for the microscopic investigation of materials. For example, angle-resolved photo-electron spectroscopy (ARPES) has allowed us to "see" the energies of occupied electron states in ever-finer detail, while neutron scattering is the ideal tool with which to reveal the magnetic properties of copper ions. The advent of high-Tc superconductors has also revealed that the theoretical model of weakly interacting electrons, which works so well in simple metals, needs to be extended. In cuprates and many other materials investigated in the last quarter of a century, we have found that the electrons cannot be treated as a gas of almost independent particles.
The result has been new theoretical approaches and also new "emergent" phenomena that cannot be predicted from first principles, with unconventional superconductivity being just one example. Other products of this research programme include the fractional quantum Hall effect, in which entities made of electrons have a fractional charge; "heavy fermion" metals, where the electrons are effectively 100 times heavier than normal; and "non-Fermi" liquids in which electrons do not behave like independent particles. So is superconductivity growing old after 100 years? In a numerical sense, perhaps – but quantum mechanics is even older if we measure from Planck's first introduction of his famous constant, yet both are continuing to spring new surprises (and are strongly linked together). Long may this continue!
The BCS theory of superconductivity
Although superconductivity was observed for the first time in 1911, there was no microscopic theory of the phenomenon until 1957, when John Bardeen, Leon Cooper and Robert Schrieffer made a breakthrough. Their "BCS" theory – which describes low-temperature superconductivity, though it requires modification to describe high-Tc – has several components. One is the idea that electrons can be paired up by a weak interaction, a phenomenon now known as Cooper pairing. Another is that the "glue" that holds electron pairs together, despite their Coulomb repulsion, stems from the interaction of electrons with the crystal lattice – as described by Bardeen and another physicist, David Pines, in 1955. A simple way to think of this interaction is that an electron attracts the positively charged lattice and slightly deforms it, thus making a potential well for another electron. This is rather like two sleepers on a soft mattress, who each roll into the depression created by the other. It is this deforming response that caused Bill McMillan to propose in 1968 that there should be a maximum possible Tc: if the lectron–lattice interaction is too strong, the crystal may deform to a new structure instead of becoming superconducting.
The third component of BCS theory is the idea that all the pairs of electrons are condensed into the same quantum state as each other – like the photons in a coherent laser beam, or the atoms in a Bose–Einstein condensate. This is possible even though individual electrons are fermions and cannot exist in the same state as each other, as described by the Pauli exclusion principle. This is because pairs of electrons behave somewhat like bosons, to which the exclusion principle does not apply. The wavefunction incorporating this idea was worked out by Schrieffer (then a graduate student) while he was sitting in a New York subway car.
Breaking up one of these electron pairs requires a minimum amount of energy, Δ, per electron. At non-zero temperatures, pairs are constantly being broken up by thermal excitations. The pairs then re-form, but when they do so they can only rejoin the state occupied by the unbroken pairs. Unless the temperature is very close to Tc (or, of course, above it) there is always a macroscopic number of unbroken pairs, and so thermal excitations do not change the quantum state of the condensate. It is this stability that leads to non-decaying supercurrents and to superconductivity. Below Tc, the chances of all pairs getting broken at the same time are about as low as the chances that a lump of solid will jump in the air because all the atoms inside it are, coincidentally, vibrating in the same direction. In this way, the BCS theory successfully accounted for the behaviour of "conventional" low-temperature superconductors such as mercury and tin.
It was soon realized that BCS theory can be generalized. For instance, the pairs may be held together by a different interaction than that between electrons and a lattice, and two fermions in a pair may have a mutual angular momentum, so that their wavefunction varies with direction – unlike the spherically symmetric, zero-angular-momentum pairs considered by BCS. Materials with such pairings would be described as "unconventional superconductors". However, there is one aspect of superconductivity theory that has remained unchanged since BCS: we do not know of any fermion superconductor without pairs of some kind.
The amazing perovskite family
Perovskites are crystals that have long been familiar to inorganic chemists and mineralogists in contexts other than superconductivity. Perovskite materials containing titanium and zirconium, for example, are used as ultrasonic transducers, while others containing manganese exhibit very strong magnetic-field effects on their electrical resistance ("colossal magnetoresistance"). One of the simplest perovskites, strontium titanate (SrTiO3), is shown in the top image (right). In this material, Ti4+ ions (blue) are separated by O2– ions (red) at the corners of an octahedron, with Sr2+ ions (green) filling the gaps and balancing the charge.
Bednorz and Müller (B&M) chose to investigate perovskite-type oxides (a few of which are conducting) because of a phenomenon called the Jahn–Teller effect, which they believed might provide an increased interaction between the electrons and the crystal lattice. In 1937 Hermann Arthur Jahn and Edward Teller predicted that if there is a degenerate partially occupied electron state in a symmetrical environment, then the surroundings (in this case the octahedron of oxygen ions around copper) would spontaneously distort to remove the degeneracy and lower the energy. However, most recent work indicates that the electron–lattice interaction is not the main driver of superconductivity in cuprates – in which case the Jahn–Teller theory was only useful because it led B&M towards these materials!
The most important structural feature of the cuprate perovskites, as far as superconductivity is concerned, is the existence of copper-oxide layers, where copper ions in a square array are separated by oxygen ions. These layers are the location of the superconducting carriers, and they must be created by varying the content of oxygen or one of the other constituents – "doping" the material. We can see how this works most simply in B&M's original compound, which was La2CuO4 doped with Ba to give La2–xBaxCuO4 (x ~ 0.15 gives the highest Tc). In ionic compounds, lanthanum forms La3+ ions, so in La2CuO4 the ionic charges all balance if the copper and oxygen ions are in their usual Cu2+ (as in the familiar copper sulphate, CuSO4) and O2– states. La2CuO4 is insulating even though each Cu2+ ion has an unpaired electron, as these electrons do not contribute to electrical conductivity because of their strong mutual repulsion. Instead, they are localized, one to each copper site, and their spins line up antiparallel in an antiferromagnetic state. If barium is incorporated, it forms Ba2+ ions, so that the copper and oxygen ions can no longer have their usual charges, thus the material becomes "hole-doped", the antiferromagnetic ordering is destroyed and the material becomes both a conductor and a superconductor. YBa2Cu3O7–d or "YBCO" (bottom right) behaves similarly, except that there are two types of copper ions, inside and outside the CuO2 planes, and the doping is carried out by varying the oxygen content. This material contains Y3+ (yellow) and Ba2+ (purple) ions, copper (blue) and oxygen (red) ions. When d ~0.03, the hole-doping gives a maximum Tc; when d is increased above ~0.7, YBCO becomes insulating and antiferromagnetic.