For centuries, physicists and mathematicians have been trying to work out the most efficient way of packing spheres in order to minimize wasted space. They think they know how to maximise efficiency in uniform packing, for example when stacking oranges. But they know less about how to improve random packing, a process that describes the behaviour of a wide range of granular materials such as sand and marbles. Now, a group of physicists in the US has modelled this random process statistically and has calculated that it can never be used to fill more than about 63.5% of available space.
Musings over sphere packing probably began in the 16th century with mathematician Thomas Harriot, a friend of the English explorer Walter Raleigh, when he tried to work out how many cannonballs could be stacked neatly on top of one another. In 1611 the German mathematician Johannes Kepler concluded that no arrangement was more efficient than the regular “face-centred cubic”, which allows a packing fraction — the fraction of overall space occupied by spheres — of 74%. This belief was proved rigorously to most experts’ satisfaction by the US mathematician Thomas Hales in 1998.
Random packing is less straightforward. There is “random close packing” which results, for example, when spherical grains are dumped in a box and then shaken. Experiments indicate that this leads to a packing fraction of 64%. But if the grains are left to settle gently, scientists instead end up with a “random loose packing” of about 55%.
Packed science
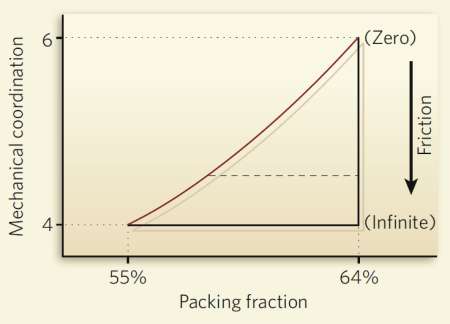
Hernán Makse, Chaoming Song and Ping Wang of the City College of New York have a theoretical model to describe random packing in detail. They assume that packed spheres obey the statistics of particles in a gas at thermal equilibrium, with a Boltzmann-like distribution of volumes. Building on research carried out by Sam Edwards of Cambridge University, they describe the volume occupied by each particle in terms of the number of neighbouring particles that it touches, a quantity known as the “geometrical coordination”. Then by inserting this equation into the statistical expression they derive a simple formula linking packing fraction to geometrical coordination (Nature 453 629).
Using their formula, the researchers have calculated that the packing fraction for random close packing is 0.634, whereas the corresponding figure for loose packing is 0.536, roughly in line with conventional wisdom. Makse and co-workers have also illustrated their formula using a phase diagram, which, they point out, highlights the crucial role of friction in random packing (see Packing phase diagram). With no friction between particles only the maximum close packing can be attained, but as friction is increased, and the geometrical coordination drops as a result, the system of particles can take on a wide range of densities. “Previously people only dealt with frictionless systems,” says Makse, “so they missed the most important part of the phase diagram.”
The researchers now plan to carry out experiments to test their model. In particular, they intend to attach polymers to tiny silica spheres in a colloid in order to generate friction between the spheres and test their ideas about the role of friction in packing. Makse points out that even if these experiments back the theory there is still more work to be done before scientists have a unified understanding of both ordered and random spherical packing. In part, that is because this latest work makes a number of shortcuts, such as modelling average particle interaction across the whole sample. “Our work is just the first step on the road to a theory on a par with that of Hales,” he adds. “The road is very long.”
Makse believes that his team’s work could have practical applications, however. He points out that granular materials are widely used in industry but that they are in fact poorly understood. He thinks that a quantity known as “compactivity” — a measure of how much a system can potentially be compacted — could help pharmaceutical, food or oil companies refine their products. “Compactivity could be used to characterize the state of a powder in the same way that temperature determines the state of a liquid or a gas,” he says.