What was once regarded as simply a mathematical curiosity could become a powerful scientific tool. That is the view of a group of geophysicists, who have found that Benford’s law – which predicts a non-uniform distribution of first digits in real-world observations – does in fact hold true across a wide range of different kinds of scientific data. The researchers believe that searching for departures from this distribution within observational data could, for example, enhance earthquake identification and improve computer simulations of the climate.
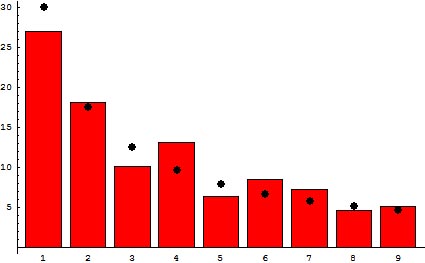
In 1938 Frank Benford generalized a proposition originally put forward by 19th-century astronomer Simon Newcomb that the first digits of numbers generated by real-world observations occur with a probability log10(1 + 1/D), where D is the value of the digit. This means that numbers beginning with the digit 1 should occur about 30% of the time in nature, while the fraction for those starting with a 2 should be about 17% and those starting with a 9 just 4%. Benford said that the prevalence of lower digits holds true no matter which base the numbers are written in and went on to show that the law, which now bears his name, applies to data describing everything from city populations to the lengths of rivers.
Malcolm Sambridge, a seismologist at the Australian National University in Canberra, says that in general the law applies to lists of numbers that are formed by some kind of additive process, in which larger numbers are less likely to occur than smaller ones. Defying many peoples’ intuitive expectation that the distribution of first digits is uniform, Benford’s law has in fact found practical application as a means of detecting fraud (since doctored numbers tend not to follow the law). “When I first tell people about the law often their reaction is that it must be a hoax,” says Sambridge. “It’s so simple that it’s bizarre, but it is in fact true.”
Gamma rays to greenhouse emissions
In the latest work, Sambridge, working with Australian National University colleague Hrvoje Tkalcic and Andrew Jackson of ETH Zürich, studied the distribution of first digits from 15 sets of data containing a combined total of more than 750,000 numbers. These data were drawn from across the sciences, ranging from the photon fluxes from distant gamma-ray sources to national greenhouse-gas emissions and the numbers of people infected with various diseases. Every one of the data sets was found to follow Benford’s law.
According to Sambridge, the law could be used to improve computer simulations of complex physical processes whose data follow the Benford distribution, such as those underlying the Earth’s climate. The researchers also believe the law could help to distinguish between earthquakes and other sources of tremors such as nuclear explosions. They found that seismic data from the earthquake behind the Asian tsunami of December 2004, collected in Peru, followed the Benford distribution, whereas the background noise preceding the earthquake did not.
Further, by analysing data collected by a seismometer in Canberra, they were able to identify a previously unobserved tiny earthquake that occurred in the Australian capital at the same time as the Asian quake. “It turns out you might not need to study seismic waveforms in detail,” adds Sambridge. “Just the first digits of the displacement data will do.”
It could apply to your data
Sambridge and colleagues urge other scientists to also scrutinize their data for the tell-tale surplus of ones. Indeed, they say, Benford’s law “is likely to hold across the sciences for data sets with sufficient dynamic range”; in other words those with a range of values that spans at least several orders of magnitude, as was the case with the data that they studied.
However, mathematician Theodore Hill of the Georgia Institute of Technology in the US sounds a note of caution. He says that Sambridge’s group provides “additional convincing evidence that Benford’s law applies across much of the sciences”, but he does not believe that dynamic range is enough to determine whether or not a data set will follow the law. Hill proved mathematically in 1995 that Benford’s law is the only possible universal law describing the distribution of digits that is invariant under changes of scale (for example, it doesn’t matter whether units are stated in metres or kilometres). But neither he nor anyone else has discovered a general principle that can predict a priori which kinds of data sets should obey the law. “The ubiquity of Benford’s law,” he says, “especially in real-life data, remains mysterious.”
This research is described in a paper recently accepted by Geophy. Res. Lett.