Is there a limit on how large a quantum superposition can be or can macroscopic objects, such as humans or say cats, also exist in a superposition of quantum states? Our daily experience seems to suggest that large objects do not obey the rules of quantum mechanics and are said to behave classically. This suggests that there could be a fundamental boundary between the quantum and classical worlds.
To try and nail down exactly where this boundary lies, researchers in Germany have tracked the motion of a large atom in an optical lattice. They found that the atom moves in a non-classical way, behaving as a quantum superposition that occupies more than one location at any given time.
Boundary conditions
Probing the classical–quantum boundary is currently of great interest to physicists, with a variety of different experiments trying to work out where such a cut-off may lie. Indeed, in the past few years, physicists have been placing ever-larger objects into states of quantum superposition. These are often interference experiments, whereby large molecules are sent through a double slit and made to interfere with themselves.
But in 1985 Anthony Leggett and Anupam Garg took a decidedly different approach to the quest by developing a theory known as “macrorealism”. Instead of showing that quantum theory holds, they aimed to show that anything apart from a quantum description would disagree with experimental observations. In explicit contrast with quantum theory, the theorists posited that in the worldview of macroscopic realism, large objects must be in one determinate macroscopic state at any given time, allowing for no superposition or blurriness in the system. Macrorealism has two main criteria: that macroscopic superpositions are not allowed and that it is possible to make a measurement of the system without influencing the system in any way, meaning that you can always measure, say, the location of a large object without disturbing it.
If macrorealism were true, repeated measurements, at different times, of a single macroscopic system would only be statistically correlated up to a certain degree, giving what they called the Leggett–Garg (LG) inequality. The aim then was to violate the inequality with experimental evidence. This is similar to the Bell inequalities, which set out to show that another basic quantum effect, known as entanglement, is indeed possible. The difference is that for Bell’s inequalities, the measurements are made at different points in space, while for the LG inequality, the experiments take place at different times. Over the years, a number of experiments on photons, nuclear spins and superconducting circuits have been carried out to violate the LG inequality.
Walk the line
“According to [macrorealism], the [object] always moves on a specific trajectory, independent of our observation,” says Andrea Alberti at the University of Bonn, Germany, explaining “The challenge was to develop a measurement scheme of the atoms’ positions which allows one to falsify macro-realistic theories.” Alberti, along with Carsten Robens also at Bonn and colleagues in the UK, has violated the LG inequality with the largest quantum objects to date. The team observed the random quantum walk of a caesium atom in an optical lattice and used a certain type of “non-invasive” measurement that gives the most stringent violation of the inequality.
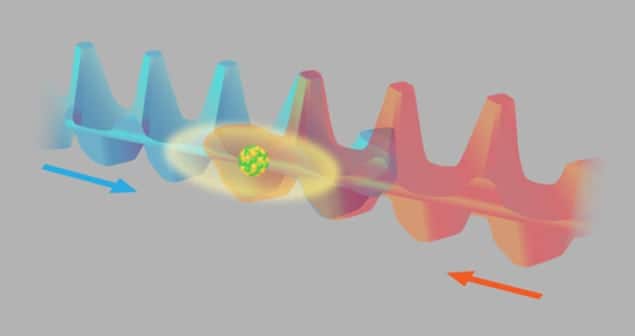
In an almost perfectly contrary manner to its classical cousin, a particle in a quantum random walk simultaneously travels in both directions – a “coherent superposition” of right and left. Over many steps, the particle is thought to be “delocalized” or blurred over many positions. Previously, researchers have seen the quantum random walk of a caesium atom. In this new work, the atom moves along one of two optical standing waves that have opposite electric-field polarizations. As it travels, the atom’s position is measured at various times, with the aim of measuring a correlation between the temporally separated positions.
To do this, the team begins by putting the atom into a superposition of two internal hyperfine spin states – this corresponds to being in both waves simultaneously. Next, the two optical waves are made to slide past each other and this makes the atom smear out or blur over a distance of up to about 2 µm – this is the quantum walk. The atom is then optically excited, and its subsequent fluorescence reveals its final location.
Cat or no cat?
Through the experiment, the researchers make three consecutive measurements. The first and the third are known – they know where the atom began its walk from, and thanks to the florescence, they known the final position. The middle measurements, which determine the internal spin-state of the atom are done non-invasively – if the atom is in one state – say, spin-up – then it is noted, but nothing is done to the experiment. If, instead, it is in spin-down state, it is transported far off so that its further evolution until the final position measurement is made cannot possibly influence the evolution of a particle that was left undisturbed. If the atom then fails to light up when the final fluorescence measurement is made, we know that the atom was in the spin-down state and was therefore discarded.
A simple way to imagine this set-up is to imagine a guessing game wherein you have two containers and under one of them is a cat. If lifting up one container reveals it is empty, we can assume that the cat is undisturbed in the second container – this is synonymous to the spin-up state. Any measurement result where the cat is seen in the container (i.e. the spin-down state) is moved away or “discarded”.
By carrying out this “null result” measurement technique in the middle step, the researchers could determine the atom’s location without directly interacting with it. By repeating this experiment many times, and seeing when the fluorescence is detected, the researchers can tell which wave the atom was in (and therefore its position) and also that the atom was not disturbed in any way. If macrorealism was true, the null measurement would not affect the outcome of the final fluorescence measurement, and the total amount of correlation of the atom’s position in time could be explained classically – but this is not the case. Indeed, the blurring that happens in the quantum walk leads to a stronger total correlation than is possible under macrorealism. This is mathematically demonstrated via the LG inequality violation, clearly showing that macrorealism cannot apply to the caesium atom.
Rainer Kaltenbaek of the Quantum Foundations and Quantum Information group at the University of Vienna, who was not involved in the current work, found the work interesting. He points out that while the superpositions created by the team were not very massive (as compared with some other experiments) they are still relatively large, being on the scale of 2 µm. This might seem tiny, but it is comparable to a human hair, which is about 75 µm across, while most bacteria are around 3 µm. Kaltenbaek also points out that “quantum physics does not perceive the [null measurement] as really ‘non-invasive’… it’s only non-invasive from a ‘realistic’ point of view.” He continues, “The authors state in their conclusions that one can still stick to a ‘realistic’ picture if one does not mind nonlocality – Bohmian mechanics is an example of that. Of course, that comes at a price – one runs into difficulties as soon as one starts thinking about relativity where ‘nonlocality’ and ‘simultaneous’ effects do not work out as nicely as in non-relativistic physics.”
The results of Alberti’s experiment seem to nail down for sure that a caesium atom obeys the laws of quantum mechanics, and that macrorealism does not apply. In the future, similar experiments with even larger masses and with longer superposition times will help to either narrow down the inherent boundary that lies between the quantum and classical world, or banish it once and for all and lay the foundations for a more advanced quantum theory.
The work is published in Physical Review X.




