A longstanding explanation for why perovskite materials make such good solar cells has been cast into doubt thanks to new measurements. Previously, physicists ascribed the favourable optoelectronic properties of lead halide perovskites to the behaviour of quasiparticles called polarons within the material’s crystal lattice. Now, however, detailed experiments at Germany’s BESSY II synchrotron revealed that no large polarons are present. The work sheds fresh light on how perovskites can be optimized for real-world applications, including light-emitting diodes, semiconductor lasers and radiation detectors as well as solar cells.
Lead halide perovskites belong to a family of crystalline materials with an ABX3 structure, where A is caesium, methylammonium (MA) or formamidinium (FA); B is lead or tin; and X is chlorine, bromine or iodine. They are promising candidates for thin-film solar cells and other optoelectronic devices because their tuneable bandgaps enable them to absorb light over a broad range of wavelengths in the solar spectrum. Charge carriers (electrons and holes) also diffuse through them over long distances. These excellent properties give perovskite solar cells a power conversion efficiency of more than 18%, placing them on a par with established solar-cell materials such as silicon, gallium arsenide and cadmium telluride.
Researchers are still unsure, however, exactly why charge carriers travel so well in perovskites, especially since perovskites contain far more defects than established solar-cell materials. One hypothesis is that polarons – composite particles made up of an electron surrounded by a cloud of ionic phonons, or lattice vibrations – act as screens, preventing charge carriers from interacting with the defects.
Measuring the kinetic energy of electrons
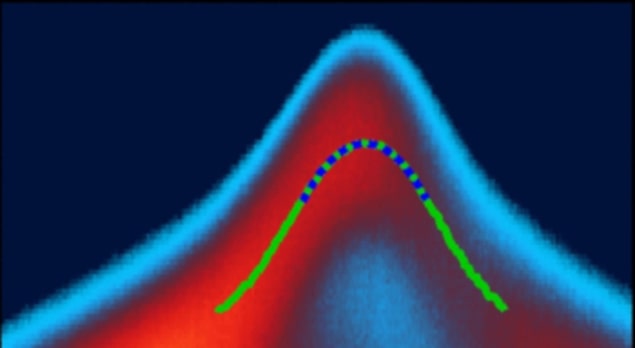
In the latest work, a team led by solid-state physicist Oliver Rader of the Helmholtz-Zentrum Berlin tested this hypothesis using a technique known as angle-resolved photoemission spectroscopy (ARPES). This technique yields information about a material’s electronic band structure via the kinetic energy E=1/2 mv2 of its electrons, where m is the electron’s mass and v is its velocity. Written in terms of the electron momentum p=mv, this relation corresponds to a parabola E=(p2)/(2m) that can be directly measured in the experiment.
If polarons are indeed present during charge transport, the electrons should move more slowly – and thus their effective mass should be higher – thanks to interactions with the polarons. The larger the electron’s effective mass, the smaller the curvature of the parabola. However, measurements led by team member Maryam Sajedi on samples of crystalline CsPbBr3 failed to identify the expected reduction in the parabola’s curvature. This was a surprise, Rader says, because theory predicted an enhancement of the effective mass by 28% in a related lead halide perovskite, while a competing experiment derived an enhancement of 50% from ARPES data.
Rader attributes the discrepancy to a combination of factors. In principle, he says, the effective mass is simple to measure, but there is an important caveat. “We measure a parabola in the binding energy versus momentum (where the momentum comes directly from the ‘angle’ in ‘angle-resolved photoemission’),” he explains. “However, in a three-dimensional solid, this parabola is a cut of a three-dimensional paraboloid, and if we do not cut it at its apex, we may obtain the wrong – usually higher – effective mass.”
Rader goes on to explain that in ARPES, the momentum in the x- and y-directions is related to the electron emission angle, but the momentum in the z-direction is determined by the energy of the photons used to excite the electrons. In BESSY II’s case, this photon energy comes from synchrotron radiation at wavelengths in the vacuum ultraviolet region of the spectrum. The main part of the experimental work was therefore finding the correct photon energy to determine the effective mass, he says.
In search of new solutions for cheap and stable solar cells
A further task was to calculate the expected effective mass without polarons. “We used an advanced method and found that previous calculations predicted a too-small effective mass,” Rader says. “The problem with this previous work was therefore half on the experimental and half on the theoretical side.”
A reliable technique
Rader notes that ARPES has previously detected an enhancement in the effective electron mass due to the presence of polarons in two non-perovskite compounds, TiO2 and SrTiO3. It is therefore a reliable technique for this type of measurement, he says. “Our conclusion is that our experimental method shows that there is no indication for formation of large polarons,” he says. “This result should lead to a reassessment of the theories that predict the presence and an important role of polarons for the properties of lead halide perovskites, most importantly their high efficiency as a solar-cell material.”
As a follow-up, the researchers say they would like to perform similar measurements on a sample of crystalline CsPbBr3 while shining light on it, but they expect this to be “challenging” experimentally. They report their present research in Physical Review Letters.




