When James Clerk Maxwell set out his famous equations 150 years ago, his model of electromagnetism included a piece of pure fiction: an invisible, all-pervasive “aether” made up of elastic vortices separated by electric charges. Margaret Morrison explores how this and other “fictional” models shape science
Too often, the word “fiction” is used to describe highly speculative hypotheses put forward by modern science. This is especially true in high-energy physics, cosmology and astrophysics (to name a few). For example, string theory is frequently slapped with the “fiction” label because it fails to make empirically testable predictions, has a tremendously large number of solutions and involves a very large set of possible universes.
But to claim that this type of research is somehow science fiction rather than physics is to misunderstand not only the role that fictional modelling has in science, but also the importance of theoretical speculation. After all, James Clerk Maxwell’s prediction of electromagnetic waves that travel at the speed of light was not testable when he made it in 1862; indeed, a quarter-century passed before Heinrich Hertz verified the existence of such waves. Similarly, when the Higgs boson was proposed in 1964 it was not testable either, and finding evidence for its existence took even longer.
Attempts to differentiate fiction from theoretical speculation give rise to an important question: how should we interpret scientific models that incorporate idealized, abstract descriptions that bear little resemblance to the physical and social world we inhabit? The question is important because much of our knowledge of physical phenomena, such as superconductivity and the Higgs boson (not to mention government decisions related to economic policy and plans for urban development), originates with model-building activities.
From an ideal world…
In some contexts, such as architectural design, models are miniature replicas of what the finished building will look like. But in other fields, models are highly idealized descriptions of phenomena that don’t (and won’t) exist in nature. For instance, many economic models presuppose that people have perfect information about the economic system they are dealing with, and that all of us make wholly rational decisions on the basis of this information. No real person is capable of such behaviour, yet the idealized human known as “rational economic man” lies at the foundation of many economic models.
Similarly, in modern physics, gases are often modelled as if they were composed of infinitesimally small molecules that have no forces acting between them, when in fact molecules do have a finite size and are subject to intermolecular forces. And in population genetics, many models assume random mating and infinite populations when calculating the effects of natural selection.
These types of modelling share a common feature: although the basis for the model is in some sense a fictional entity (one that doesn’t exist in reality), we know how to add corrections to the model to bring it closer to actual situations. We can adjust economic models in ways that incorporate relevant but less than perfect information; we can add mass and forces to gas models to make them more realistic; and we can use approximation techniques to adjust for populations that are very large but not infinite. Hence, although these models are fictional, there are strategies available that enable us to use them to explain and predict features that interest us.
But while I have used the word “fictional” to describe these models, this is somewhat of a misnomer. The model-maker’s goal is not to create a fictional representation and see how (or whether) it compares with reality. Rather, the process of creating an ideal, abstract version of a system is often a way of making models more mathematically tractable, or of focusing on properties of interest for the problem at hand. For instance, when we want to model fluid flows, we do not take account of quantum properties; in fact, we sometimes don’t even take account of frictional forces. Instead, the fluids are modelled in an “ideal” way. So in some sense, models of this type are not really fictional at all, because their aim is to provide accurate information about real phenomena.
…to an imaginary one
Many models used in physics, economics, biology and other sciences involve descriptions that are fictional in a stronger sense. Models of this type cannot be said to describe real phenomena even in principle, regardless of how many parameters or approximations are added. For example, fictional models frequently occupy centre stage in econophysics, a field that uses physics techniques to study the dynamical behaviour of financial and economic markets. In statistical econophysics, economic agents are treated like microscopic particles in statistical physics: they are modelled as having no intelligence; their behaviour is completely random; and the mathematical outputs of the model are analogous to diffusion reaction models in physics. In this case the fictional, unrealistic aspects of the model(s) are its essential features, and part of its very structure. Moreover, there is no question of adding realistic parameters to it, since the model’s fictional status is the reason it functions in the first place. Not only does it enable the user to manipulate large data sets in a relatively simplified way, it also highlights various aspects of financial markets that had not previously been studied in traditional economic analysis. These include phenomena such as the inverse relation between market stability and the range of financial instruments available for facilitating trades.
Some models cannot be said to describe real phenomena even in principle, regardless of how many parameters are added
It is possible, of course, to object to this example on the grounds that the use of some econophysics modelling techniques was partly responsible for the financial crisis in 2008. For example, the famous Black–Scholes model, which describes how the prices of stocks and other financial instruments vary over time, assumes that price changes follow a Gaussian distribution where the probabilities of extreme effects are negligible. Unfortunately for the world’s investors, wildly fluctuating markets – like physical systems exhibiting critical behaviour – resist this type of modelling. Instead, they require tools from dynamical systems theory (specifically renormalization group techniques) that allow for “fat-tailed” non-Gaussian distributions of price changes that take account of strongly correlated events. However, it is important to remember that these other tools are also idealized. Hence, it wasn’t the use of highly idealized models that was the culprit in the financial crisis; rather, it was the use of the wrong type of model for the problem at hand.
Another example of the usefulness of fictional modelling can be found further back in the history of physics. To derive his famous field equations for electromagnetism, Maxwell relied on a model of the aether – the supposed carrier of light waves – that consisted of rotating elastic vortex cells separated by electrical particles. We know now that the aether does not exist, and Maxwell himself referred to his model as “imaginary”. However, it nevertheless enabled him to formulate the equations governing electromagnetic phenomena, and to show that light and electromagnetic waves are one and the same.
Under these circumstances, it seems natural to ask how a fictional structure can deliver information about real concrete physical systems or financial markets. How do we get from a model that is “false” to information that is true or reliable?
Turning fiction into reality

To see how a fictional structure can give rise to reliable explanations, let us look at Maxwell’s work in more detail. His four equations – which appeared together for the first time in his 1861–1862 paper “On physical lines of force” (Philosophical Magazine, available online at http://ow.ly/scEDk) – describe the electric and magnetic fields arising from varying distributions of electric charges and currents, and how those fields change in time. Before Maxwell, accounts of electromagnetic phenomena had been based on (among other things) Ampère’s law, which related the magnetic field to its electric current source. In addition, Michael Faraday had put forward the idea that the seat of electromagnetism was in the spaces surrounding wires and magnets, rather than in the objects themselves. Faraday used iron filings to visualize the patterns of electromagnetic forces in space, referring to their spatial distribution as “lines of force” that constituted a “field”.
Maxwell hoped to build on this work by creating a model that showed how electromagnetic phenomena could be accounted for in terms of a field rather than by charged objects (which he interpreted as “centres of force”) acting at a distance. He wanted to develop these ideas in a visualizable but mathematically precise way – a process that involved formulating equations that could describe the propagation of electromagnetic waves through space. This was especially challenging because, at the time, light waves were thought to be distinct from electromagnetic phenomena, and while there was supposedly an aether that carried light waves, no such structure existed for electromagnetic waves. So how could a fictional model enable Maxwell to derive field equations that ultimately identified light with electromagnetic waves?
To find the answer, we need to understand how the model first allowed Maxwell to mechanically represent wave propagation in a field, and then enabled him to formulate the proper mathematical equations describing behaviour such as the build-up of charge – all without any appeal to explanations involving charged objects. Maxwell constructed his model by assuming that the aether was composed of elastic “vortex cells”, separated by electrical “particles” that acted like idle wheels in a system of gears (figure 1). These particles were assumed to exert tangential forces on the surfaces of the vortices, causing the vortices to deform. The resistance of the vortices to this deformation resulted in an inertial reaction force on the particles, which Maxwell identified as electromotive force.
1 Wheels within wheels
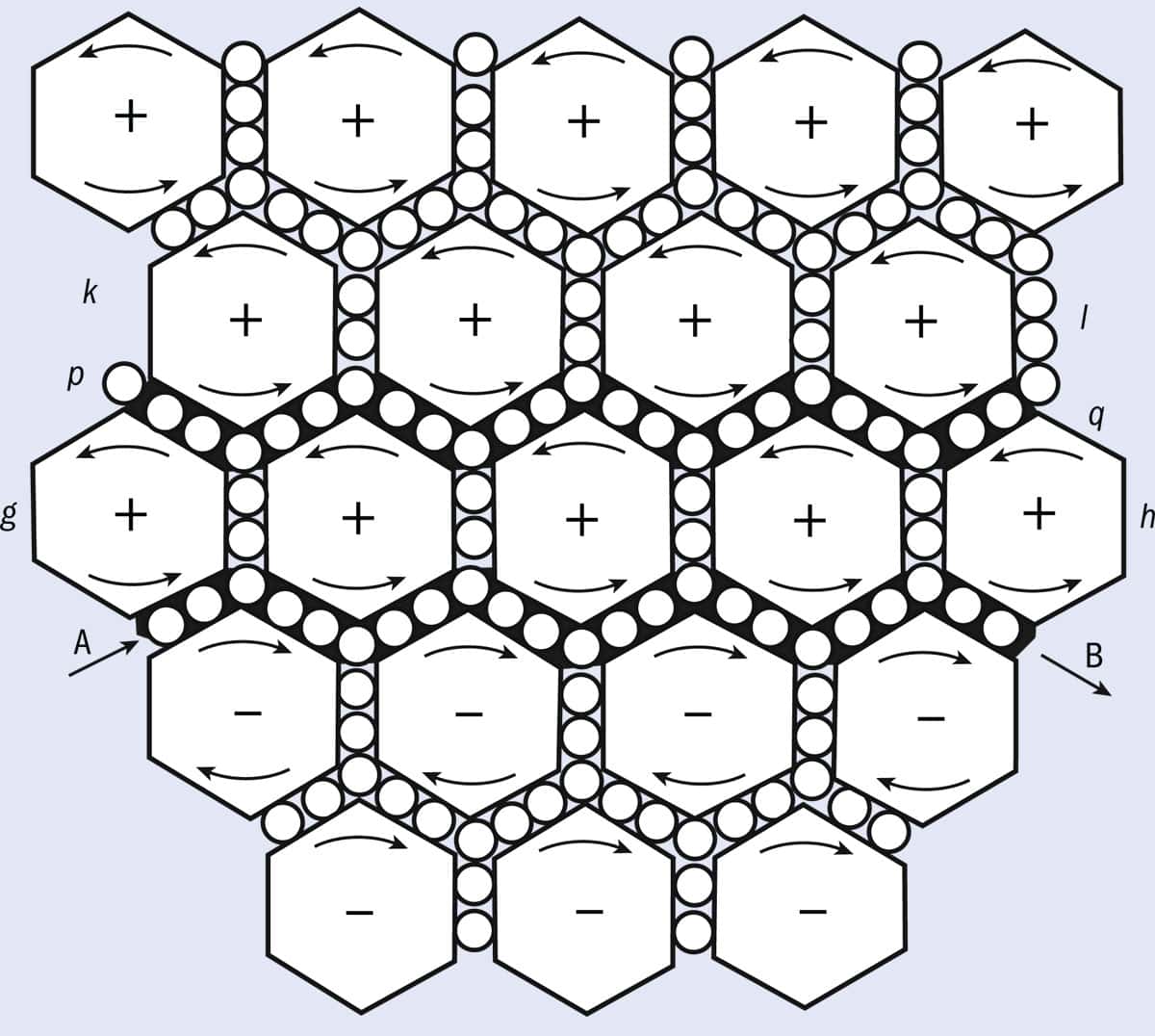 James Clerk Maxwell’s schematic diagram of his model of electromagnetism, which hypothesized an aether filled with elastic vortices (represented by large hexagonal spaces) and surrounded by electrical particles (small circles) that acted as idle wheels. In the model, interactions between the vortices and the particles give rise to electromotive force, electric current and displacement current. If a current flows between point A and point B, the row of vortices labelled g–h will be set in motion in an anticlockwise direction (denoted +). The layer of particles p–q will be acted on by the g–h vortices, causing them to move in a clockwise (–) direction from right to left – thereby forming an induced electric current. If this current is checked by the electrical resistance of the aether, the rotating particles will act on the row k–l of vortices, causing them to also revolve in the (+) direction. This movement continues until the vortices reach a velocity such that the motion of the particles is reduced to simple rotation, resulting in the disappearance of the induced current.
James Clerk Maxwell’s schematic diagram of his model of electromagnetism, which hypothesized an aether filled with elastic vortices (represented by large hexagonal spaces) and surrounded by electrical particles (small circles) that acted as idle wheels. In the model, interactions between the vortices and the particles give rise to electromotive force, electric current and displacement current. If a current flows between point A and point B, the row of vortices labelled g–h will be set in motion in an anticlockwise direction (denoted +). The layer of particles p–q will be acted on by the g–h vortices, causing them to move in a clockwise (–) direction from right to left – thereby forming an induced electric current. If this current is checked by the electrical resistance of the aether, the rotating particles will act on the row k–l of vortices, causing them to also revolve in the (+) direction. This movement continues until the vortices reach a velocity such that the motion of the particles is reduced to simple rotation, resulting in the disappearance of the induced current.
When the vortex cells in Maxwell’s model rotated, their rotation set the particles between them in motion. This movement of particles was, naturally, interpreted by Maxwell as an electric current. However, Maxwell also reasoned that the progressive distortion of the vortices would cause the particles to move in the direction of the distortion (figure 2). This motion would produce an elastic restoring force that led to a reverse polarization, and hence a reverse current. Maxwell identified the distortion of the vortex cells as the displacement of electricity, and the current that resulted from it came to be known as the displacement current.
We can see how Maxwell’s model worked by considering a basic circuit for charging a parallel-plate capacitor. When current flows through the circuit, electric charge will gradually build up on the capacitor plates. Maxwell’s model accounts for this behaviour by suggesting that progressive distortion of the vortices in the space between the plates – and the displacement current such distortion produces – causes tension to build up in the aether. Maxwell identified this build-up of tension with electric charge.
The capacitor example is important because it represents a situation not covered by the original formulation of Ampère’s law, which involved only closed circuits. But if electromagnetic waves were capable of travelling through space, as they do when current flows through the space between the capacitor’s plates, then an additional term – the displacement current – needed to be added to Ampère’s law to account for the free transmission of electricity. It was this displacement term that essentially represented the field theoretical features of electromagnetism.
Maxwell used this model of elastic, deformable vortices and the accompanying displacement of electricity as a basis for deriving his electrostatic force law. In doing so, he was able to account for the fact that a changing magnetic field induces an electric field and a changing electric field induces a magnetic field. This, in turn, led to his crowning achievement, which was not just to show that the electromagnetic field was responsible for the propagation of electromagnetic waves, but to calculate that the velocity of such waves coincides with that of light. Ultimately, what the various mechanisms in the model provided was a way of showing how electricity could travel in free space – all on the basis of a fictitious representation.
2 A build-up of tension
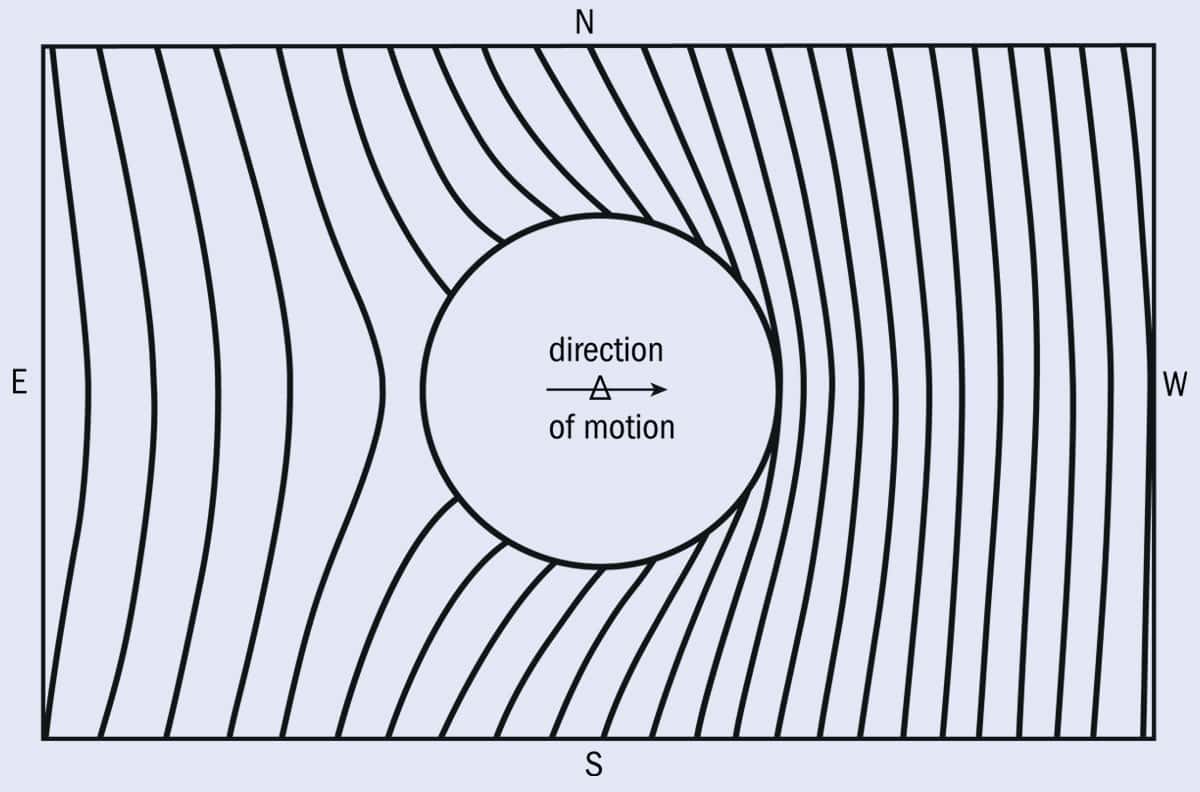 In James Clerk Maxwell’s diagram of his model of electromagnetism, the motion of the particles produces a distortion in the aether.
In James Clerk Maxwell’s diagram of his model of electromagnetism, the motion of the particles produces a distortion in the aether.
Seeking generalizations
In Maxwell’s case, the route from fictional model to reality came via the fundamental mechanical features of the model, such as the vortices, the electrical particles and the ways they interacted. These features constrained how the physical and mathematical aspects of electromagnetic forces could be described, in much the same way as character development in a novel determines, to some extent, how the story will play out. In other words, the model furnished a “possibility structure” that helped bring into being the mechanical laws and equations representing the behaviour of electromagnetic field phenomena.
Of course, it remained for experiment to decide whether those equations matched reality. But understanding how the fictional model could function in this way requires a careful analysis of the model itself, one that includes both the kind of information the model yields and how that information can be used to develop physical hypotheses and predictions. Although the fictional representation supposedly bears a certain structural similarity to physical reality (for example, both obey mechanical laws) the model functioned as a self-contained entity in Maxwell’s investigations. The model, rather than some experimental reality, was the object of inquiry, and predictions were made about the electromagnetic field on the basis of its output.
This example suggests that the answer to our question about how fictional models provide accurate information is that there is no general answer. The process takes place in a way that is specific to the particular model and system under investigation. For example, not all models display the kind of mechanical intricacy that Maxwell’s did. A good example is the comparatively simple Ising model, which is used in explaining the behaviour of magnets and other types of phase transitions. It consists of a set of magnetic spins arranged on an abstract mathematical structure called a lattice. How such mathematical structures provide information about physical systems is also an important question for understanding scientific modelling. To answer that question we need to know how mathematics relates to the world. But are mathematical entities real? Or are they, too, a kind of fiction?