For over 200 years physicists have tried to pin down the value of the gravitational constant. Jon Cartwright finds out what’s been taking them so long

It was back in 1982, during his PhD, when Clive Speake first understood the true nature of gravity. “It was amazing,” he recalls fondly. “I remember going out the night I had done the experiment for the first time, and I just looked up at the Moon. It had given me a completely different feel for what the Moon is, you know? Why it’s there.”
Such epiphanies are not uncommon among those who perform measurements of the gravitational constant. Gravity is the most famous of nature’s forces, because it is the one that is most obviously present in our lives. Ever since Isaac Newton was inspired by a falling apple, everyone has known that it is gravity behind the inevitable phrase “what goes up, must come down”. Yet despite our familiarity with gravity, few of us have experienced the force other than when it is directed towards the ground beneath our feet.
To see why, you need only look at the numbers. Gravity is the weakest force – 1036 times weaker than electromagnetism, the force that governs most other everyday phenomena. The only reason we can feel gravity on Earth is because it scales with mass: our planet’s mass of five zetta-tonnes (5 × 1021 tonnes) is enough to bring gravity into the realm of normal human perception. But the force still exists between all other objects, and if you do ever witness it with Earth out of the equation – for example, in the faint shift of two suspended metal weights – it might at first seem like magic. “It’s a liberating experience,” says Speake, who is now based at the University of Birmingham in the UK.
Liberating – and infuriating. The gravitational constant – “big G”, as it is commonly known – is what characterizes the strength of gravity according to Newton’s law, and it is fiendishly difficult to measure. Experiments struggle to deliver uncertainties much smaller than one part in ten thousand – compare that, for instance, with the proton–electron mass ratio, which is known to four parts in ten billion.
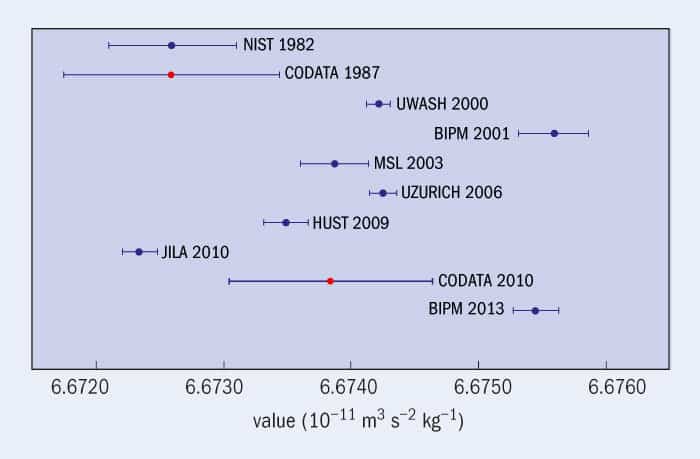
Low precision alone is enough to keep a metrologist up all night. But in recent years, a much more serious problem has arisen: measurements of big G are in wild disagreement with one another (figure 1). Since the turn of this century, values recorded by some of the best labs in the world have been spread apart by more than 10 times their estimated uncertainties. Something is amiss – yet no-one is quite sure what. “You go over it, and over it, and over it,” says Speake. “And there comes a time when you say, I just can’t think of anything we’ve done wrong.”
A massive task
On the face of it, an experimental determination of big G should be straightforward. Newton’s law states that the gravitational attraction between two bodies is proportional to the product of their masses, and inversely proportional to the square of the distance between them (F = Gm1m2/d2). To generate the biggest force possible, therefore, one needs very big masses, very close together.
Of course, there are various other considerations. The masses ought to be made of homogenous materials, for instance, so that their centres of mass can be accurately located. It is also prudent to keep the apparatus small and seal it in a container, to avoid convection currents generated by temperature changes. But the biggest consideration is so-called “little g”: the last headache an experimentalist needs is to measure not only the gravitational force between their test masses, but also the Earth’s own gravitational pull.
In 1798 the British scientist Henry Cavendish famously evaded the little-g problem using a torsion balance he had inherited from the geologist John Michell (see “The saga begins”). A torsion balance consists of a vertical wire attached at its bottom to a horizontal beam, suspended on the ends of which are two known “test” masses. On either side of these a pair of larger, “source” masses is suspended separately. Once rotated a little from their starting position, these source masses cause the test masses to rotate due to gravitational attraction. Crucially, this rotation is perpendicular to – and thus unaffected by – the Earth’s own gravitational pull, because the masses all hang vertically.
The rotation of the test masses twists the central wire, which in response exerts a restoring torque; at some angle, this torque matches the masses’ gravity. By measuring this angle and knowing the torque generated for a given angle, Cavendish could estimate the gravitational force. Due to older unit conventions, Cavendish did not turn this into a value for big G, but his result is easily expressed in that form.
After Cavendish’s experiment, not much changed in 200 years – at least in terms of basic apparatus. There were modifications, such as the use of vacuum cans to exclude air resistance, and the use of materials with low susceptibilities to avoid magnetic effects. But by the early 1980s, physicists believed they had honed the torsion-balance technique so well as to settle on big G’s true value: an experiment performed by Gabriel Luther and William Towler at the US National Bureau of Standards (now known as the National Institute of Standards and Technology, or NIST) in Washington, DC, gave big G as 6.673 × 10–11 m3s–2kg–1 to within 75 parts per million (ppm) – a value that was subsequently adopted by the Committee on Data for Science and Technology (CODATA), which provides the internationally accepted values of the fundamental constants.
A second opinion
For about a decade, all was well. Then in the mid-1990s Winfried Michaelis and others at the Physikalisch-Technische Bundesanstalt (PTB) in Braunschweig, Germany, published what they believed to be a more reliable determination of big G. In place of a torsion wire they used a low-friction liquid bearing, the torque of which could be imposed electrically. The researchers calculated a value for big G of 6.715 × 10–11 m3s–2kg–1 – a whopping 50 standard deviations greater than the CODATA value.
Either CODATA or the PTB group was wrong, but which? The problem with absolute measurements is that there is no default answer to fall back on. This is unlike null experiments, in which experimentalists look for a deviation from zero to see whether or not some effect is present – an example being the LIGO team in Washington state and Louisiana, US, which is patiently waiting for the appearance of laser interference that would signal the first direct detection of a ripple in space–time, or gravitational wave. “Most of the very precise experiments are null experiments – or differential measurements, where you’re measuring the difference between two things,” says Stephen Merkowitz at NASA’s Goddard Space Flight Center in Maryland, US. “But absolute measurements are very hard, because of all the calibrations involved.”
Merkowitz was one of many physicists who, in the wake of the PTB discrepancy, decided to measure big G for themselves. Working then at the University of Washington in Seattle, US, he and his colleague Jens Gundlach came up with an alternative design for a torsion balance in which a torsion pendulum and its associated test masses are rotated continuously on two separate turntables. The acceleration of the inner turntable holding the torsion pendulum could be adjusted to keep the torsion wire itself from twisting. Then, by monitoring the feedback to the inner turntable, the researchers could read off the gravitational force from the circling test masses and thus determine a value for big G.
Part of the appeal of this apparatus was that there could be no errors deriving from wire properties – particularly “anelasticity”, in which a wire’s stiffness changes with the frequency of twisting. As a result, Gundlach and Merkowitz could record an uncertainty of just 14 ppm. And yet, prior to their publication in 2000, they still had doubts. “We worried a lot,” says Merkowitz. “Were we forgetting something? And it’s true, we could have.”
Actually, there was good reason to worry. While their value for big G was lower than the PTB group’s, it was still far beyond the error bars of the official CODATA value. And further experiments did not clear up the situation. The next year, a group at the International Bureau of Weights and Measures (BIPM) in Sèvres, France, led by Terry Quinn and including Speake – who had retained a keen interest in precision tests of gravitation since his PhD work – measured big G using two different methods. They performed a torsion-balance experiment using both Cavendish’s technique of measuring the maximum angular deflection, and a new “servo” method in which the masses’ gravitational attraction is balanced by a measured electrostatic torque, such that the torsion balance does not move. Despite the combined result having a small uncertainty of 41 ppm, its value was 200 ppm above Gundlach and Merkowitz’s.
At least half a dozen other experimental groups had a go. In 2006 Stephan Schlamminger and colleagues at the University of Zurich in Switzerland found a similar value to the Washington group. But in 2010 Harold Parks and James Faller at JILA, an institute shared between NIST and the University of Colorado in Boulder, found big G to be 280 ppm below the Washington group’s – though oddly in line with the original CODATA value. The irony was that, by this time, the outlying PTB value that instigated the rush of these new measurements had been written off as a result of some stray capacitance.
Gaining support
Ask the group members what the true value of big G is, and they all have confidence in their own measurements. But then they all speak highly of the other determinations, too. “It’s always difficult if you ask an experimentalist,” says Schlamminger. “They’ll say, ‘I know the true value of big G because I measured it!'”
Some would argue that the most reliable measurements are those that have been corroborated. Schlamminger and colleagues’ value, which agrees with the Washington group’s, has the distinction that it was based on a very different method, involving a beam balance. Used, for instance, by pharmacists, a beam balance consists of a sealed box containing a mass pan, which can measure weights to very high precision.
Schlamminger and colleagues modified their beam balance so that each of the two test masses could be hung from it: the first two metres below, and the second four metres below. This separation allowed the researchers to place two huge, 500 litre tanks of mercury either between the test masses, or above and below them. By measuring the weight differences between the test masses with the mercury tanks in each position, the researchers could extract a value of big G to within 16 ppm that was consistent with the Washington group’s.
The corroboration was looked upon favourably by CODATA, which in 2010 issued a new official value for big G that was close to the Zurich and Washington groups’ values, although with large error bars. To some in the gravity community, it seemed as though a new consensus was finally taking shape.
It wouldn’t last long. Quinn, who had retired as director of the BIPM in 2003, had already persuaded his old lab to support another big G experiment, to see whether his group’s abnormally high result using two different methods had been a fluke. When they accepted, he didn’t hang around. “I devoted almost all my time to it,” he says. “You just ask my wife; she was not very pleased.”
Between 2003 and 2007, Quinn, Speake and colleagues rebuilt almost all their apparatus. They executed an unprecedented number of checks and calibrations, which involved calculating the gravitational influence of every component, down to the last screw. Again, they calculated big G using both the Cavendish and servo method, to exclude a majority of systematic errors. But their result, published last September, was a shock: it was almost exactly as high as before (Phys. Rev. Lett. 111 101102).
The situation now among big G experiments is a spread of values that scarcely overlap. Which raises the question: what will CODATA do when it meets again this August to assess the values of the fundamental constants? “The answer is, I don’t know,” says Quinn. “I have to say, I am a member of the CODATA panel that evaluates this, but I shall have to leave the room when they talk about it.”
Human error
Could some sort of new physics be to blame, in which, for example, the value of big G changes depending on location in space–time? Few researchers think so: the spread of values is too inconsistent to suggest a new force is at work. But some have pointed to a phenomenon that could explain the discrepancy: intellectual phase-locking – or, in simple terms, seeing what you want to see. “People might say, ‘Terry, you were an experimentalist in both of these [BIPM experiments],'” says Quinn. “‘Did you somehow arrange it that you got the same answer?’ Well, maybe I did – but we tried to take steps to avoid that.”
Those steps were, essentially, to keep each of the different input parameters under wraps until the last minute, so that it would be impossible for any of the BIPM experimentalists to pre-empt the final value. And Quinn’s group was not the only one concerned about such a possibility. “A lot of groups lose sleep in the run up to publishing a value,” says Merkowitz. “Even if it agrees with another group’s, you think: are we just stopping our analysis now, because it agrees? Or do we need to keep digging, looking for something else? Because you’re never sure what the real value is.”
Faller believes intellectual phase-locking is impossible to rule out. “Physicists don’t like to get the wrong answer,” he says. “You look over your shoulder, and you think, ‘Oh my God! The last five people who measured it got a number that was higher than my group! What did I do wrong?’ That’s not the way to do science – but it is the way real people do science.”
Even if intellectual phase-locking has biased some values, it has not prevented the overall discrepancy, and it is for this reason that most of those involved assume that the systematic errors have not all been taken into account. Speake quotes the former US defence secretary Donald Rumsfeld, who famously said there are “known unknowns” and “unknown unknowns”. Unfortunately, each of the groups is confident its error bars are allowing for these unknowns. “I feel like we’ve got it right,” Speake says. “But I can’t point a gun at the other people and say, ‘You’ve got it wrong.’ Because I don’t know enough about their experiments.”
For that, journals could be partly to blame. Physical Review Letters, the journal in which most big G results have been published, usually limits papers to four pages; by comparison, Cavendish’s original torsion-balance paper is 57 pages long. Many of those in the gravity community believe they have not had the opportunity to properly pick apart one another’s techniques.
Fortunately, that opportunity may have finally come. This month, the Royal Society will convene a meeting at Chicheley Hall in Newport Pagnell, UK, of most of those involved in the recent measurements of big G. The hope is that the meeting will allow the metrologists to decide on the most likely sources of systematic error and, ideally, think up an experiment that would avoid them. Many of those contacted by Physics World revealed they already have ideas for new experiments – although they were not necessarily keen on performing them themselves. “I say you should never do the same experiment twice,” says Schlamminger. “I mean, what would you do if you contradicted yourself?”
Yet like most metrologists who have tried to determine big G, Schlamminger refuses to give up the challenge. “It’s difficult to measure it – that’s why I want to measure it,” he says. “You know, why do people climb Mount Everest? Because it’s difficult.”