Cooling atoms to ultra-low temperatures reveals the striking differences between fermions and bosons at the quantum level.

When the 2001 Nobel Prize for Physics was awarded to Eric Cornell and Carl Wieman from JILA in Boulder, Colorado, and to Wolfgang Ketterle from the Massachusetts Institute of Technology, they were recognized for creating and studying Bose-Einstein condensates – dilute gases of atoms that are all in the same quantum state. Their remarkable achievement enabled “quantum gases” to be studied experimentally for the first time, and jump-started new sub-fields of research, including gaseous superfluidity, atom lasers and matter-wave optics.
Cornell, Wieman and Ketterle’s research centred on atoms that were bosons – particles with integer spin. But physicists have since extended their work to create Fermi gases made from atoms that are fermions – particles with half-integer spin. Interestingly, the constituents of matter – protons, neutrons and electrons – are all fermions, whereas a composite particle, such as an atom, is a boson if the total number of protons, neutrons and electrons is even, and a fermion if the total number is odd.
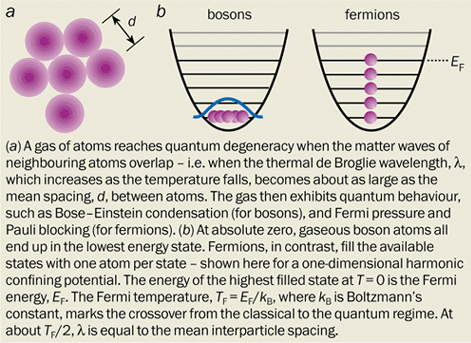
Fermions and bosons are very different at the quantum level. As Wolfgang Pauli’s famous exclusion principle states, identical fermions cannot occupy the same quantum state at the same time. Bosons, however, can share quantum states. But to observe this fundamental difference, gases of bosons or fermions have to be chilled to ultra-low temperatures, where individual quantum states have a high chance of being occupied. At these low temperatures, bosons will eagerly fall into a single quantum state to form a Bose-Einstein condensate, whereas fermions tend to fill energy states from the lowest up, with one particle per quantum state (figure 1). At high temperatures, in contrast, bosons and fermions spread out over many states with, on average, much less than one atom per state.
Another difference is that fermions do not undergo a sudden phase transition in the ultra-low temperature regime. Instead, the quantum behaviour emerges gradually as the fermion gas is cooled below the Fermi temperature TF = EF/kB, where EF is the Fermi energy – the energy of the highest filled state – and kB is Boltzmann’s constant. TF, which is typically less than 1 µK for atomic gases, marks the crossover from the classical to the quantum regime.
The odd quantum behaviour of fermions permeates all of physics, and is responsible for phenomena ranging from atomic structure to the stability of neutron stars. But unlike other Fermi systems found in nature, a Fermi gas of atoms occurs in a new, ultracold, low-density regime where interparticle interactions are weak. Dilute gases of atoms also provide an exquisite environment in which to investigate, probe and control quantum phenomena – as has been amply demonstrated by the wealth of beautiful experiments carried out on Bose-Einstein condensates in recent years (see Triple first for Bose condensates by Christopher Foot Physics World May 2001 pp21-22).
Cooling fermionic atoms
The main experimental challenge in creating a fermionic gas is to chill the atoms to ultra-low temperatures. Given the fact that physicists have been able to cool bosons to microkelvin temperatures since 1995, when Bose-Einstein condensates were first created, one might think that experiments to cool fermions would have followed soon afterwards. However, cooling a gas of fermionic atoms is difficult because of their strange collision properties.
In general, collisions play a crucial role in the physics of quantum gases. Elastic collisions, for example, keep the gas in thermal equilibrium as it cools. These collisions also affect many of the properties of both Bose-Einstein condensates and Fermi gases by determining the interparticle interactions. However, differences in the collisional behaviour of bosonic and fermionic atoms arise at temperatures well above those that are required for the gas as a whole to behave quantum mechanically.
Typically, atoms in an ultracold gas will only collide if they approach each other head-on in what is known as an “s-wave” collision, where there is no relative angular momentum between the two atoms. But due to the Pauli exclusion principle, these s-wave collisions are forbidden for fermions that are in the same internal quantum state – i.e. that have the same spin-state. This lack of collisions makes it impossible to cool such a fermionic atomic gas efficiently.
However, fermionic atoms that are in different internal states can collide through s-wave collisions (see box). This means that it is, after all, possible to cool fermions to near absolute zero, as my colleague Brian DeMarco and I showed in 1999, when we created the world’s first quantum-degenerate Fermi gas of atoms.
The strange collision properties of fermions
Fermi gases in practice
In our experiments, we adapted techniques that had already been developed by physicists to create Bose-Einstein condensates. We began by collecting a sample of potassium-40 atoms from a room-temperature vapour and cooling them in a “magneto-optical trap”. This gave us about 500 million atoms at a temperature of 150 µK. We then loaded atoms in two different internal spin-states into a magnetic trap where they could be cooled still further.
However, holding atoms with two different spin-states in a magnetic trap is tricky. The trap has a field minimum and can therefore only confine those atoms with a magnetic moment that points in the opposite direction to the magnetic field – so-called weak-field seeking states. In our experiments at JILA we used potassium-40 atoms in the lowest energy hyperfine ground state, where the total atomic spin, f, is 9/2. A particle with spin 9/2 has 10 spin-states (mf = -9/2, -7/2, -5/2…+9/2), the energies of which are split in a magnetic field by the Zeeman effect; half of these spin-states are weak-field seeking and could, in principle, be confined in a magnetic trap. We decided to use the two spin-states with the largest magnetic moments – mf = +9/2 and mf = +7/2 – because they do not undergo inelastic collisions that would leave them in the lower-energy states that cannot be trapped.
Once we had stably confined the mixture of atoms with two spin-states in the magnetic trap, we evaporatively cooled them to below 300 nK. This technique works in much the same way as a cup of hot coffee cools: the highest energy atoms in both spin-states in the experiment are removed from the trap, lowering the temperature of the remaining gas in the process. Once the Fermi gas had reached the quantum regime, we obtained information about it by turning the magnetic trap off, allowing the gas to expand and measuring the shadow of the gas cast by a laser. These absorption images let us determine the energy, temperature, number and momentum distribution of the atoms in the gas.
This approach, pioneered by my group at JILA, is not the only way of obtaining ultracold Fermi gases. Randy Hulet and his group at Rice University (see Truscott et al. in further reading), as well as Christophe Salomon and co-workers at the Ecole Normale Supérieure (ENS) in Paris (see Schreck et al. in further reading), have used a technique known as “sympathetic cooling”, in which a gas containing a mixture of isotopes – rather than a mixture of spin-states – is cooled. Both groups have used this approach to cool mixtures of lithium-6 and lithium-7 atoms. The lithium-7 atoms, which are bosons, are evaporatively cooled in the usual way. Meanwhile, the simultaneously trapped lithium-6 atoms, which are fermions, cool simply by being in thermal contact with the boson gas – just as hot coffee would cool if placed in contact with ice.
Sympathetic cooling has also been used to create Bose-Einstein condensates using bosons with two different spin-states or two different isotopes. As well as introducing another method of cooling fermionic atoms, these experiments have enabled mixtures of bosons and fermions to be studied. In a third experiment, using lithium-6, John Thomas and co-workers at Duke University have used an all-optical trap to confine and cool a mixture of atoms in two spin-states (see O’Hara et al. in further reading).
Quantum degeneracy
Using these novel experimental techniques, physicists have been able to cool Fermi gases of atoms into the quantum-degenerate regime below the Fermi temperature, TF. But because the effects of quantum statistics become stronger as a gas is cooled further into this regime, the ultimate cooling limit is an important issue. Experiments at JILA using potassium-40 in two spin-states, and at Rice and the ENS in Paris using lithium-6, have so far cooled atoms to about 20% of TF. We do not yet know why potassium-40 atoms cannot be cooled any further, although the quantum nature of fermions as well as technical challenges could both play a role.
In the experiments on lithium at Rice and the ENS, however, sympathetic cooling is limited by the formation of lithium-7 Bose-Einstein condensates. The effectively attractive interactions between lithium-7 atoms make the condensate collapse, causing atoms to leave the trap. The fermions can therefore no longer cool by being in contact with the boson gas.
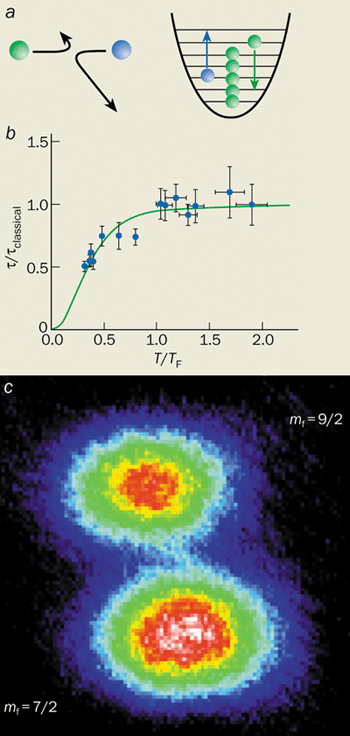
The quantum behaviour of an atomic Fermi gas was first revealed in thermodynamic measurements. At JILA we study the atomic Fermi gas by analysing absorption images of the expanded gas. As the gas expands, fast atoms travel further from the centre of the gas than slow-moving atoms. An optical image of the gas therefore reveals the momentum distribution of the atoms: those atoms with low momentum remain near the centre of the cloud, while atoms with high momentum appear at the edges.
We have used this technique to show how a Fermi gas of potassium-40 atoms enters the quantum regime. When the gas is cooled below TF, the number of particles with low momenta (i.e. near the centre of the image) falls below the value expected from classical physics. This is a sign of quantum behaviour. Only one fermion is allowed to occupy each quantum state, which means that the low-energy states are quickly filled and the other fermions must therefore fill states of higher and higher energy. Indeed, experiments reveal that the mean energy per particle rises well above the classical value (figure 2a).
Hulet and co-workers at Rice, as well researchers at the ENS, have carried out similar experiments to show the differences in size between a Fermi gas (lithium-6) and a Bose gas (lithium-7). In the quantum regime, the mean energy per fermion rises above the value expected from classical physics or in a Bose gas. The fermion atoms have more kinetic energy, which means that the trapped Fermi gas spreads over a larger volume than the Bose gas (figure 2b). This quantum phenomenon, called Fermi pressure, is seen in astrophysics and is responsible for stabilizing white-dwarf and neutron stars against their gravitational potential.
Interactions in a Fermi gas of atoms
Physicists studying Bose-Einstein condensation soon realized that interactions between the atoms play a key role in determining properties such as the size and even the stability of the condensates. Indeed, the differences between condensates made from rubidium, sodium or lithium atoms depend simply on the strength of the interparticle interactions at ultra-low temperatures and whether these interactions are attractive or repulsive. Such interactions can also play an important role in Fermi gases. In our work at JILA, for example, we have used potassium-40 atoms in two spin-states to create a two-component interacting Fermi gas, in which we have observed the effect of a strange phenomenon known as “Pauli blocking”.
Occurring in all Fermi systems, Pauli blocking is a consequence of the fact that identical fermions can never occupy the same quantum state. A fermionic atom can therefore only change energy – in a collision, for example – if the final energy state is unoccupied. But in the quantum regime, it is highly likely that low-energy states are already occupied. Pauli blocking therefore tends to suppress any process in which atoms change energy states.
We have observed Pauli blocking by measuring “collective excitations” of the trapped gas (figure 3). These excitations, which are essentially sound waves, involve small relative motions between the two different gases in our samples. They provide valuable information about how the atoms in a Fermi gas collide. Indeed, collective excitations have proved to be a very valuable way of studying other quantum fluids. They have been widely used to characterize Bose-Einstein condensates – for example to investigate interactions, to probe finite temperature effects, and even to detect superfluidity and vortices. In an atomic Fermi gas, Pauli blocking of collisions is revealed by changes to the “damping time” for collective excitations. What is particularly interesting about Pauli blocking is that it is a quantum-mechanical effect in which collisions are affected by atoms that are far away from one another.
Fermi gases – the future
Even though the study of Fermi gases of atoms is still in its infancy, it is clear that this new field complements research into Bose-Einstein condensation. While experiments on Fermi gases have already revealed a number of striking effects of quantum statistics, cooling the gas further into the degenerate regime could enhance the quantum effects still further. Several other quantum effects that have been predicted – such as a dramatic change in the interaction of the gas with light – remain to be explored experimentally.
So where do we go next? The lack of collisions in a single-component Fermi gas of atoms could be exploited for precision measurements of these atoms, while recent experiments on two-component Fermi gases have begun to study the interplay of interactions and quantum statistics in determining behaviour. Fermionic atoms could also be loaded into “optical lattices” – three-dimensional egg-box-like arrays of potential wells created by the interference of multiple laser beams. This would give researchers an almost ideal model of solid-state systems, with the potential wells acting like lattice sites in a crystal and the fermionic atoms sitting in the wells.
Yet another new opening is the study of Bose/Fermi hybrid systems. In addition to the mixed-isotope lithium experiments discussed previously, several experimental groups are working toward realizing Bose/Fermi mixtures with different atoms. Ketterle and co-workers at MIT, for example, have recently demonstrated quantum degeneracy in a mixture of bosonic sodium atoms and fermionic lithium atoms. Other researchers, such as Massimo Inguscio and colleagues at the European Laboratory for Nonlinear Spectroscopy in Florence, Italy, as well my group at JILA, are working with mixtures of rubidium and potassium atoms.
Arguably the most exciting prospect in the study of Fermi gases is the possibility that there might exist a new phase transition to a superfluid state. Even before Fermi gases of atoms were created in the laboratory, this notion had been explored by theorists such as Marianne Houbiers and Henk Stoof from the University of Utrecht in the Netherlands. Similar phase transitions exist in many condensed-matter systems, including the transformation of liquid helium-3 into a superfluid. The eerie phenomenon of superfluidity – flow without viscosity – was first seen in liquid helium-4, where its appearance was relatively easy to explain. The superfluidity is due to the fact that helium-4 atoms are bosons and so can occupy a single quantum state by forming a Bose-Einstein condensate. Superfluidity in liquid helium-3, however, cannot be explained as simply because the atoms are fermions.
Another example of this type of phase transition for fermion systems is the technologically important phenomenon of superconductivity. Here the fermionic condensates occur through the creation of a small number of “Cooper pairs”, each consisting of two weakly correlated fermions. Although fermions have half-integer spin, the two together have integer spin, making the Cooper pair a “composite boson”. Just as in Bose-Einstein condensation, the Cooper pairs can fall into a single quantum state and thus cause a phase transition to a superconducting or superfluid phase.
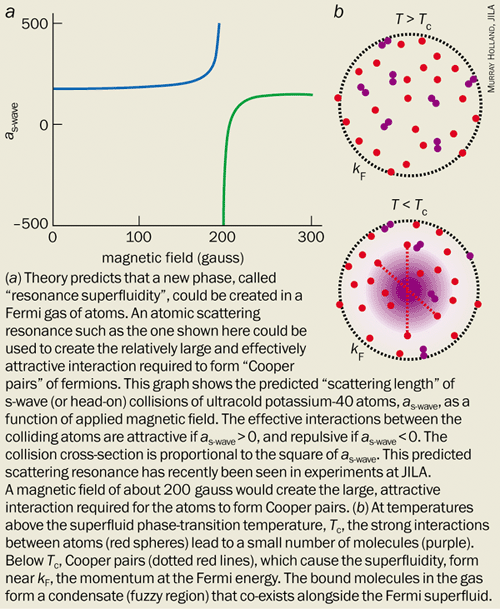
Cooper pairing of atoms in a gas would provide a new and unique example of a fermionic condensate. In all known examples of this quantum phenomenon, the pairing interaction is extremely weak and the phase transition occurs at temperatures many orders of magnitude below the Fermi temperature. However, recent theoretical work by Murray Holland at JILA and by Eddy Timmermans at the Los Alamos National Laboratory in New Mexico has suggested that a superfluid phase-transition temperature, Tc, in an atomic gas could be as high as TF/2. Ironically, compared with condensed-matter examples of fermionic condensation, the predicted phase transition in a Fermi gas of atoms would have both the highest relative temperature (compared with TF) and the lowest absolute temperature.
Such a high-Tc system would require a complex, non-trivial theory and the fermionic atom condensate is likely to have many exciting new properties (see Holland et al. and Timmermans et al. in further reading). The system could be created by using a “scattering resonance” to enhance the interactions between the fermionic atoms. This would lead not only to Cooper pairs of fermionic atoms, but also to a small number of bound molecules in a condensate that exists alongside the Cooper pairs (figure 4). By varying the resonant interactions, it may be possible to explore – in the same system – the crossover from physics based on the Bardeen-Cooper-Schriefer theory of superconductivity to the physics of Bose-Einstein condensates made from tightly bound composite bosons.
Experimentalists are already trying to realize this transition to a superfluid state. If they succeed, it could help us to understand not only high-temperature superconductivity, but also the underlying connection between it and Bose-Einstein condensation. It is clear that research into Fermi gases still has very much to offer.