Physicists are exploring the ear's ability to hear both faint whispers and loud cries, and to distinguish between similar musical notes.
We naturally think of our ears as receivers for sound, so it came as a major surprise when, in 1979, David Kemp of University College London found that ears can also emit sounds. A sensitive microphone placed close to the eardrum typically records a faint hum, but in many human subjects clear whistles can be picked up on top of the background buzz. In rare pathological cases, these sounds can be loud enough to be heard by passers-by!
Kemp’s experiments clearly showed that something within the ear was vibrating, and they heralded a new era of hearing research. Since then, researchers have thought of the ear as an active receiver. This research is now entering an exciting phase. An understanding of the cellular basis of the ear’s power source is emerging, and the fundamental physics of active-signal detection is being worked out.
The occurrence of “otoacoustic emissions” was not a complete surprise to everyone, however. As long ago as 1948 Tommy Gold, a young researcher then at Cambridge, had foreseen that the ear employs an active process. He pointed to a problem with the classical theory of hearing that had been formulated by the German physicist Hermann von Helmholtz in the middle of the 19th century.
Helmholtz believed that the ear responded to sounds in much the same way that a harp string resonates when a singer hits the right note. He supposed that the inner ear contained a set of “strings”, each of which vibrated at a different frequency. We now know, however, that the detection apparatus resides within the cochlea, a fluid-filled duct that is coiled like a snail’s shell. Given the microscopic size of the putative strings, the viscous damping of the fluid would prevent the build up of a resonant response.
Gold argued that an active process must somehow counteract the friction, so that sharp frequency tuning and high gain can both be achieved. Without these capabilities, the ear would not be able to distinguish similar frequencies or to hear faint sounds. He therefore proposed that the ear operates rather like a regenerative radio receiver. Invented by the radio pioneer Edwin Armstrong, this device works by adding energy at the very frequency that it is trying to detect. It was clear to Gold that such a mechanism must be very delicate, however, as it would require a positive feedback of precisely the right magnitude to cancel the damping. Any less and the ear would be insensitive; any more and it would ring spontaneously.
Wave mechanics
Elegant though it was, Gold’s hypothesis fell on deaf ears. No doubt disenchanted by the inertia of scientific thought, he turned to cosmology, where the inventiveness of his ideas was better appreciated. The attention of hearing researchers shifted, instead, to the fluid mechanics of the cochlea, attracted by the results from a series of remarkable experiments conducted in the 1930s and 1940s by Georg von Békésy at the laboratories of the Hungarian Post Office.
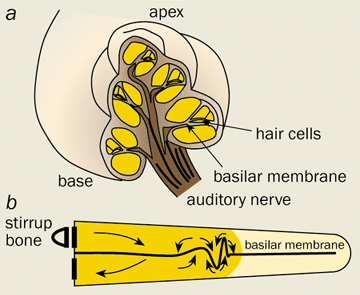
With great technical prowess, Békésy succeeded in imaging the minute displacements of the “basilar membrane”, the flexible partition that extends along almost the entire length of the cochlea, dividing it into two separate channels (see figure 1). He discovered that a sound stimulus entering the inner ear causes a wave-like distortion to propagate along the basilar membrane. As the wave advances, its amplitude increases and its wavelength decreases until it reaches a place of maximal disturbance, after which it decays rapidly. Crucially, the location of the maximum depends on the frequency of the stimulus, with high frequencies peaking near the base of the cochlea and lower frequencies travelling further towards the apex.
Békésy’s observations suggested that a simple “place code” might be used to convey information about the pitch of a stimulus to the brain. The movement of the basilar membrane is monitored by sensory hair cells, which produce neural spikes in the auditory nerve when they are displaced. Information about the major frequency components of the stimulus can therefore be gleaned from the location of the nerve cells that fire most rapidly.
The basic physics of the travelling wave can be described by a simple one-dimensional transmission-line model – an approach instigated by Josef Zwislocki in a thesis that was published the same year as Gold’s hypothesis. A sound stimulus rattles the tiny hammer, anvil and stirrup bones that lean against the oval window at the entrance to the cochlea, thus setting the cochlear fluid in motion (figure 1b). Owing to the incompressibility of the fluid, variation in the longitudinal flow must be accompanied by lateral motion of the basilar membrane. This movement is caused by the pressure difference that develops between the two channels as a result of the fluid flux. These mutual interactions between the fluid and the membrane generate a slow wave that travels from the base towards the apex.
The most striking feature of the basilar membrane is its elasticity. As it has very little longitudinal rigidity, adjacent sections of the membrane can move almost independently of one another, being coupled only through the fluid. Moreover, the membrane’s lateral stiffness varies greatly along its length, decreasing by about two orders of magnitude from the base to the apex of the cochlea. This changing stiffness means that the wave propagation is “dispersive”. As the wave advances, its wavelength decreases and it slows down.
In regions where the damping is negligible (i.e. near the base) the wave must grow in amplitude to conserve the flow of energy. At some point, however, the motion of the basilar membrane becomes fast enough for viscous drag to become significant. This characteristic place is near the base of the cochlea for higher frequencies. Beyond this point, the damping steals energy from the wave and its amplitude quickly declines.
Mystery of the ear’s acuity
A major problem with this view of cochlear mechanics is that it gets nowhere near to explaining the ear’s astonishing performance, which exceeds even that of our visual system. The quietest sounds that we can hear impart no more energy per cycle than thermal noise does and, according to Békésy’s results, would displace the basilar membrane by only a fraction of an ångström.
At the same time, the ear can cope with a vast range of sound levels; loud noises that cause pain carry over 12 orders of magnitude more energy than the faintest whispers. In addition, the cochlea is an excellent frequency analyser; we can distinguish two tones that differ by a few per cent in frequency if they are played simultaneously, and a fraction of a per cent if they are played successively. The place code is far too coarse a mechanism to account for this acuity. How, then, does the ear achieve the remarkable feat of distinguishing semitones and hearing both cries and whispers?
Békésy’s discovery of the travelling wave merited the 1961 Nobel Prize for Physiology. But we now appreciate that the cochlea operates in a much subtler way than his experiments revealed. Békésy made his measurements on cadavers and, in order to obtain a detectable response, he had to blast sound at 140 decibels – enough to make the dead jump out of their skins.
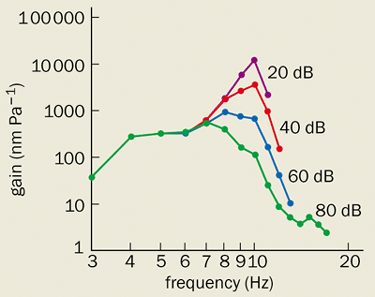
Even before Kemp’s discovery of otoacoustic emissions, the relevance of Békésy’s data was called into question by a remarkable experiment by William Rhode at the University of Wisconsin. In 1971 Rhode succeed in making measurements on a live cochlea for the first time. Using the Mössbauer effect to measure the velocity of the basilar membrane, he made a significant discovery. The frequency tuning was far sharper than that reported for dead cochleae. Moreover, the response was highly nonlinear, with the gain increasing by orders of magnitude at low sound levels. The ear’s sensitivity had finally been revealed, although its physical origin remained unclear.
It took another decade to repeat these delicate experiments, but in recent years much more accurate measurements obtained using laser interferometry have confirmed Rhode’s findings (figure 2). There is an active amplifier in the cochlea that boosts faint sounds, leading to a strongly compressive response of the basilar membrane. When the power supply of the ear is interrupted, this amplification ceases. Stone dead equates to stone deaf.
What is the source of the activity? Potential candidates began to appear in the 1980s, as a result of careful experiments that measured the properties of individual cells in the living ear. The first evidence of active movement was found right at the heart of the detection apparatus, in the hair bundles that act as mechanical sensors.
A hair bundle is an appendage measuring a few microns across that sticks up above the surface of every hair cell. It is composed of a bundle of columnar “stereocilia”, which slope up against one another. The tip of each hair is connected to the next by a fine filament called a “tip link” (see figure 3). Shear flow in the cochlear fluid causes the whole bundle to deflect, with each stereocilium pivoting at its base so that the tip links get stretched. Each tip link connects directly to a tension-gated “transduction channel” in the cell membrane of the stereocilium, which admits potassium ions. So the deflection leads to a change in the ionic current that, in turn, alters the cell potential.
This very direct mechanism for converting motion into electrical signals was established by numerous researchers in the 1980s and 1990s. Jim Hudspeth, now at Rockefeller University, and David Corey of Harvard University made particularly important contributions by developing methods to manipulate frog hair bundles with microneedles and measure the transduction current.
In 1985 Andrew Crawford and Robert Fettiplace, then at Cambridge University, discovered that hair bundles in turtle ears could oscillate spontaneously. That same year, William Brownell and colleagues at Baylor College of Medicine in Texas discovered a second source of motion that is particular to the mammalian cochlea. In addition to the inner hair cells, mammals also have a second source called the outer hair cell, which is also crowned by a hair bundle. Brownell and his co-workers found that outer hair cells are electromotile; when a voltage is applied, the whole cell body contracts longitudinally by a few per cent. Subsequently Jonathan Ashmore, then at Bristol University, measured the speed of the outer-hair-cell motor and showed that it could respond to oscillating voltages at several kilohertz.
Hopf resonators
Experimental investigations into the cellular basis of the active amplifier in the ear have stimulated theoretical physicists to revive Gold’s ideas and develop them further. Two groups, one based at Rockefeller University and the other involving researchers at the Institut Curie in Paris and Cambridge University, including the author, have proposed models based on the theory of dynamical systems. Both groups argue that the inner ear contains a set of motile systems – most likely the hair bundles themselves – each of which is capable of generating oscillations at a particular frequency (see Camaletet al. and Eguiluz et al. in further reading).
When one of these nonlinear dynamical systems is on the verge of vibrating, it is especially sensitive to periodic disturbances at frequencies close to its characteristic frequency. The onset of spontaneous oscillations corresponds to what is known as a “Hopf bifurcation” in the language of dynamical-systems theory. This is a critical point at which the behaviour of the system suddenly changes from still to vibrating.
Critical points also exist in equilibrium phase transitions, such as vaporization. Near these points, the behaviour of the system is universal and does not depend on the microscopic details. The same is true of dynamical transitions. This means that the response of the cochlea can be characterized without any detailed knowledge of the physical apparatus that generates the oscillations.
A critical Hopf oscillator acts as a nonlinear power amplifier, boosting weak signals much more than strong ones. In fact, the displacement of the oscillator varies as the cube root of the stimulus force, so the gain grows indefinitely as the signal falls to zero. This compressive nonlinearity explains how the ear manages to cover such a large dynamic range. The 120-decibel variation in sound levels that we can comfortably hear can be detected by displacements of hair bundles that vary by only a factor of 100.
The Paris-Cambridge team has gone on to describe how these motile systems can be set up so that they are poised on the brink of an oscillatory instability. The researchers demonstrated how a simple feedback control mechanism could automatically adjust each system to its critical point, where its response is most sensitive.
Such a self-tuning mechanism provides a natural explanation for spontaneous emissions of sound from the ear. Normally, the low-amplitude vibration of the self-tuned critical oscillators would produce a faint hum. But if one of the motile systems were to have a faulty control mechanism, it might oscillate wildly, generating a shrill whistle.
According to this theoretical work, a choir, rather than a harp, is a better analogy for the way the ear operates. One can think of the cochlea as containing many “voices”, each of which is ready to sing along with any incoming sound that falls within its own range of pitch.
Location of the motor
Hearing researchers are now working hard to establish the physical basis of dynamical oscillators and to understand the nature of the self-tuning mechanism. After all, it is perfectly plausible that different organisms use different apparatus to implement the same general strategy.
Several researchers tried to recreate Crawford and Fettiplace’s experiment with frog hair cells in vitro, with little success. Indeed, it has always been tricky to reproduce spontaneous bundle oscillations in dissected specimens. The situation changed when Pascal Martin and Jim Hudspeth at Rockefeller succeeded in making preparations in which the extracellular ionic concentrations were carefully adjusted to correspond to physiological conditions. Following this breakthrough, they discovered that low-amplitude spontaneous oscillations could be observed quite readily. Their work confirmed that the motile system resides within the hair bundle (in frogs, at least) and provided evidence that a feedback control mechanism involving calcium ions adjusts the system close to the oscillatory instability.
What might be generating the oscillations? One potential source, suggested by Yong Choe, Marcelo Magnasco and Hudspeth at Rockefeller, is the transduction channels themselves, which can displace the hair bundle as they open and close to admit potassium and calcium ions. A second obvious candidate is the molecular motor myosin – a variant of the protein molecule that drives our muscles. These molecules, which are attached to the transduction channels, have long been implicated in the bundle’s ability to adapt to changing conditions because movement of the motors resets the tension in the tip links. However, myosin molecules are also in a perfect position to shake the bundle.
Molecular motors generate force and motion by continually binding and breaking down energy-releasing molecules at a rate of about 100 molecules per second. One objection that had been raised in the past is that this rate is too slow for motors to cause oscillations at audio frequencies. However, Frank Jülicher and Jacques Prost at the Institut Curie have demonstrated that if a number of motors work together, they can collectively generate oscillations at frequencies much faster than their individual rates.
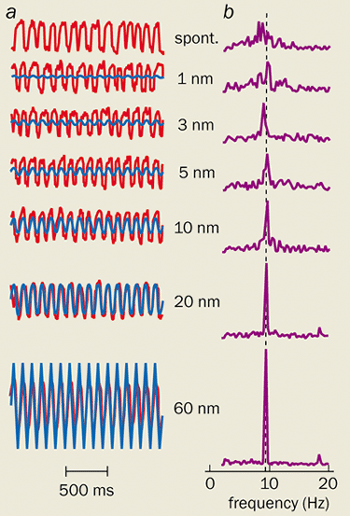
The most convincing evidence to date that hair bundles act as Hopf oscillators comes from a recent experiment by Martin (who is now at the Institut Curie) and Hudspeth. Using a microneedle to shake a bundle, they measured its response to a sinusoidal force. What they found bore all the hallmarks of the Hopf resonance (see figure 4).
Their observations also support the arguments of the Paris-Cambridge theorists about how the ear detects signals below the threshold for thermal noise. Even though such weak stimuli are too feeble to increase the amplitude of the bundle’s noisy motion, they do make the oscillations slightly more regular. This “phase-locking” is apparent in the timing of the potential spikes in the auditory nerve. It appears that a great deal of information about frequency must be encoded by the time intervals between spikes, and that this “time code” might be at least as important as the place code.
In the mammalian cochlea, the outer hair cells are widely believed to power the movement of the basilar membrane. It remains unclear, however, whether the outer-hair-cell motor is itself a Hopf oscillator, or whether it is simply an additional linear amplifier that boosts oscillations generated by the hair bundle. Spontaneous oscillations of an outer hair cell have never been observed. Nevertheless, great strides have recently been made in understanding the physical basis of its electromotility.
Arguing that the cell membrane must contain a large quantity of molecular motors, Peter Dallos and his colleagues at Northwestern University looked for genes that are abundantly, but exclusively, “expressed” in outer hair cells. Such genes would be translated into the right type of protein. Dallos and co-workers found a gene that, when introduced in cultured kidney cells, caused the cells to change their shape in response to voltages.
The identification of this gene product, which they named prestin in honour of the rapidity of the outer-hair-cell motor, opens new avenues for research into the mechanism of electromotility. One possibility is that extensive arrays of the prestin protein act as piezoelectric elements that change the surface area of the cell, driving its expansion and contraction.
Cochlear waves and sound processing
The realization that outer hair cells pump the basilar membrane is also leading to a revised theory of cochlear mechanics. A decade after proposing the existence of quarks, theorist George Zweig of the California Institute of Technology turned his talents to hearing research and discussed how sound energy can be transported to a localized place in the cochlea without any reflection taking place. In the 1980s his theoretical analysis of the cochlear travelling wave was extended by James Lighthill of University College London.
Essentially, the group velocity of the wave must fall to zero at that location, dropping in such a way that there is sufficient time for the damping to dissipate all of the wave’s energy before it gets to that point. Zweig and Lighthill showed that this could happen if each section of basilar membrane responds as a lightly damped oscillator. However, as Gold pointed out, the magnitude of the viscous forces is likely to forbid this possibility.
In a model of the active cochlea devised by Jülicher and the author, the membrane is considered to be an excitable medium driven by a set of “self-tuned” critical oscillators (which probably correspond to individual outer hair cells). By exactly cancelling the friction at just one place – the location where the oscillator frequency matches the sound frequency – the active oscillators cause the wave to stop at that point. The resulting active travelling wave has a very sharp peak, the amplitude of which grows as the cube root of the sound level. An alternative model that combines the action of a travelling wave and the Hopf resonance has been proposed by Magnasco at Rockefeller.
Theoretical analyses such as these, coupled with ongoing experiments, should help to establish the physical basis of the cochlear tuning curve shown in figure 2. A fascinating new tool that promises to help in this task is a miniature microphone built by Elizabeth Olson at Princeton University, which permits the pressure wave in the cochlear fluid to be measured precisely.
Another fruitful area of research concerns the way in which the ear processes complex sound signals. For example, what is the relative importance of place coding and time coding? A better understanding of how frequency and volume are represented in the auditory nerve would help to improve the design of cochlear implants, which bypass the impaired hair cells of the profoundly deaf and stimulate the nerve directly with electrodes.
While the Hopf resonance is ideal for detecting a single frequency, its intrinsic nonlinearity causes two or more tones to interfere with one another in the cochlea. Jülicher at the Institut Curie and the author’s group in Cambridge have investigated the Hopf response to two tones and have shown that it accounts for the two main physiological manifestations of interference. The first of these is called two-tone suppression: the presence of one tone tends to diminish the response of the cochlea to a second tone of similar frequency.
The second type of interference is the generation of distortion products. When two tones are played simultaneously, the response of the basilar membrane includes a whole spectrum of frequencies: the two original frequencies f1 and f2 are present, but so are all frequencies equal to f1 + n(f1 – f2), where n is an integer. These distortion products become increasingly important as the two frequencies approach one another.
A number of perceived or psychoacoustic effects may be directly associated with these nonlinearities. For example, the 18th-century violinist and composer Giuseppe Tartini was the first to remark that the pitch 2f1 – f2 could be heard when two notes are played simultaneously, even though that frequency is absent in the sound waves. This auditory illusion is probably caused by the most prominent of the distortion products that the cochlear amplifier generates.
Music to our ears
Even our notion of musical harmony might be attributable to the physical nature of the ear’s detection apparatus. Pythagoras famously discovered the enigmatic relation between the “consonance” of musical intervals, which forms the basis of musical scales, and the ratios of small integers. Harmonies are most pleasing when the frequencies of the notes are simply related, while non-integer ratios sound grating or dissonant. (The notes in a perfect fifth, for example, have a frequency ratio 3:2.)
Pythagoras’s disciples considered this to reflect a greater harmony in the universe. But Helmholtz claimed that consonances are simply less-jarring dissonances – an explanation that chimes better with our modern sensibilities. He ascribed the sensation of dissonance to the close mismatches in frequency that occur between harmonics when notes are played on a musical instrument. If the fundamentals are in integer ratios, such mismatches are fewer and the sound is sweeter.
But why should two tones with slightly different frequency sound rough? The active amplifier may be the reason. By creating pronounced distortion products, it makes the hair bundle oscillate in a complex manner with an amplitude that is modulated by non-sinusoidal beats. This makes it difficult for the brain, which has only the spike timings to go on, to deduce the original frequency components of the sound.
Such an interpretation coincides with the composer Arnold Schoenberg’s view that “what distinguishes consonance from dissonance is not a greater or lesser degree of beauty, but a greater or lesser degree of comprehensibility”. Had not the ear evolved to capture the crack of a twig beneath a predator’s paw, our appreciation of music might have been very different.