The rotation of quantum objects has a long and distinguished history in physics. In 1912 the Danish scientist Niels Bjerrum was the first to recognize that the rotation of molecules is quantized. In 1938 Edward Teller and John Wheeler observed similar features in the spectra of excited nuclei, and suggested that this was caused by the nucleus rotating. But a more complete explanation had to wait until 1951, when Åage Bohr (the son of Niels) pointed out that rotation was a consequence of the nucleus deforming from its spherical shape. We owe much of our current understanding of nuclear rotation to the work of Bohr and Ben Mottelson, who shared the 1975 Nobel Prize for Physics with James Rainwater for developing a model of the nucleus that combined the individual and collective motions of the neutrons and protons inside the nucleus.

What makes it possible for a nucleus to rotate? Quantum mechanically, a perfect sphere cannot rotate because it appears the same when viewed from any direction and there is no point of reference against which its change in position can be detected. To see the rotation the spherical symmetry must be broken to allow an orientation in space to be defined. For example, a diatomic molecule, which has a dumbbell shape, can rotate about the two axes perpendicular to its axis of symmetry.

A quantum mechanical treatment of a diatomic molecule leads to a very simple relationship between rotational energy, E, and angular momentum. This energy is found to be proportional to J(J + 1), where J is the angular momentum quantum number. The molecule also has a magnetic moment that is proportional to J.

These concepts can be applied to the atomic nucleus. If the distribution of mass and/or charge inside the nucleus becomes non-spherical then the nucleus will be able to rotate. The rotation is termed “collective” because many of the nucleons (the protons and neutrons) are involved. These nucleons follow well defined orbits inside the nucleus, just like electrons in an atom. The stability of a particular nucleus is closely related to the energies of these orbits. Small changes in the spatial alignment of these orbits lead to changes in the angular momentum (or spin) of the nucleus. Like molecules, nuclei have magnetic moments that are proportional to their angular momentum for a fixed configuration of nucleons.

Rotation in nuclei

The most spectacular examples of collective rotation occur in “superdeformed” nuclei. These nuclei have ellipsoidal shapes in which the major axis is twice as long as the minor axis, like a rugby ball or an American football. If the moment of inertia of the nucleus remains constant – in other words if it does not change its shape or structure – then the energy levels still obey the simple quantum mechanical relationship E ∝ J (J + 1).

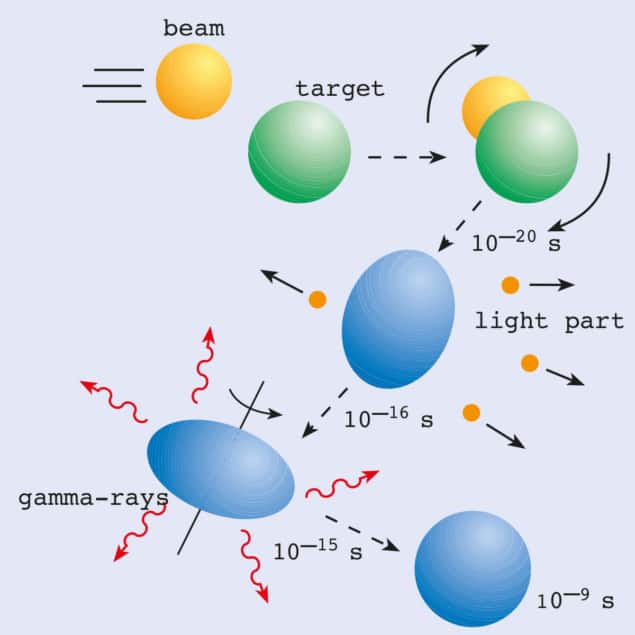
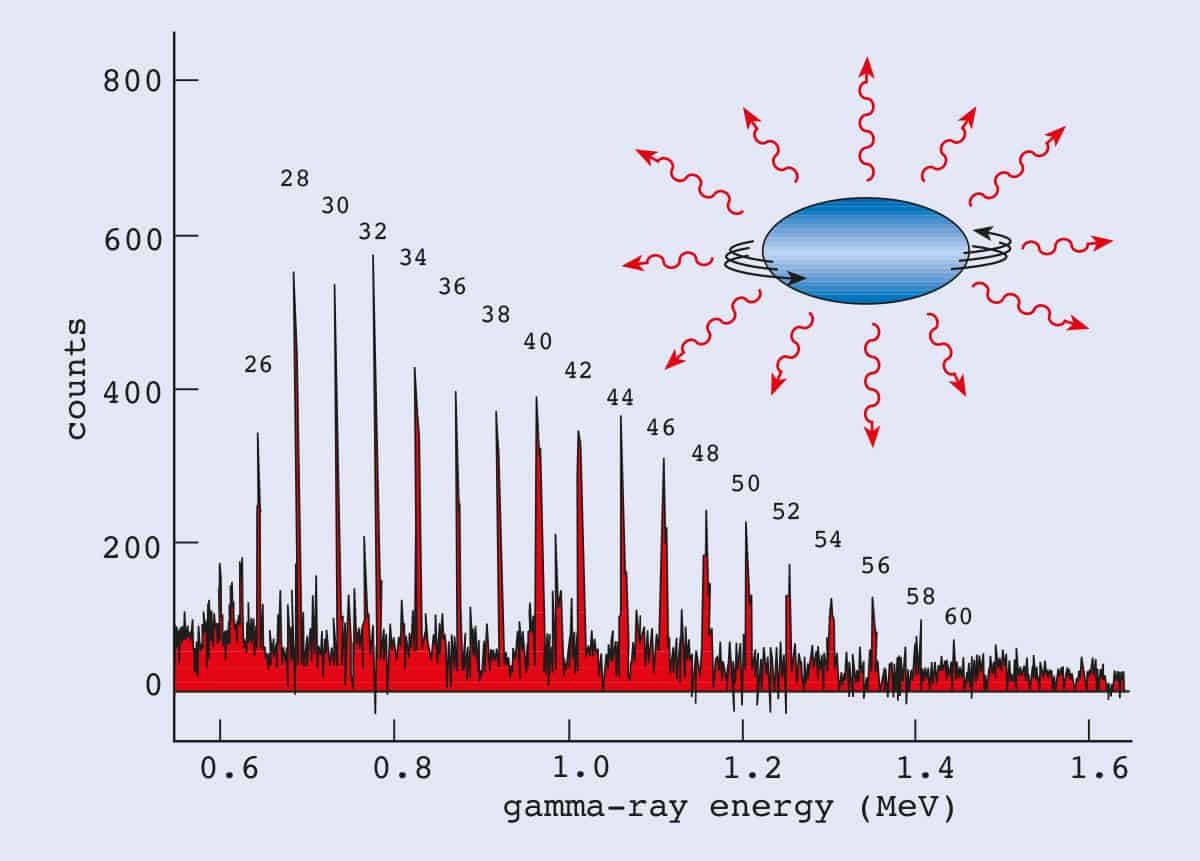
To populate the high angular momentum states in a nucleus, such as the superdeformed states, a thin metal foil is bombarded by high-energy ions (figure 1). When a nucleus in the beam strikes a nucleus in the target foil, they can fuse together to create a “hot” compound nucleus. At first the nucleus loses energy by emitting light particles, such as neutrons, protons or alpha particles. Then, when its energy falls below the energy binding the particles together, it cools further by radiating gamma-rays. Since the energy levels of the deformed nucleus are regularly spaced, the gamma-rays form a characteristic “band” or “picket fence” spectrum (figure 2). Only about 1% of the nuclei formed in these collisions go through a superdeformed stage.

The nucleus is thought to maintain its extreme shape as it loses angular momentum and energy. After emitting approximately 10–20 gamma-rays the superdeformed nucleus, which is still highly excited, decays into states associated with a near-spherical shape that have about the same angular momentum but much less energy. The final decay process between these two shapes is still only partially understood.

A superdeformed nucleus emits electric quadrupole radiation – each photon carries an angular momentum of 2ħ and has a gamma-ray energy of ħω/2, where ħ is the Planck constant and ω is the rotational frequency of the nucleus. To think of this classically, imagine a metal rugby ball that is charged, spinning on its short axis. When either end of the ball is pointing towards an observer, the electromagnetic field is stronger than when a side of the ball faces the observer. Therefore, the field oscillates twice for every complete revolution of the rugby ball. A superdeformed nucleus spins incredibly quickly, about 10²¹ times per second, and by the time it has decayed to the ground state, which takes about 10^-9 s, the nucleus will have completed more revolutions than the Earth has done since it was formed.

Patterns of gamma-rays from superdeformed nuclei were first identified in 1986 at the Daresbury Laboratory in the UK in a collaborative project headed by Peter Twin of Liverpool University. Since then, powerful new spectrometers have been built to detect weak gamma-ray decay, including spectra from other examples of superdeformed nuclei. The latest generation of large detector arrays include “Euroball”, which has been built by a collaboration of 30 nuclear physics groups in Europe, and “Gammasphere” in the US. Euroball was designed to be moved to various nuclear physics facilities in Europe and is currently at the Legnaro National Laboratory in Italy. Gammasphere moved from the Lawrence Berkeley National Laboratory to the Argonne National Laboratory earlier this year.

Stability in the nucleus

The nucleus is often considered to behave like a drop of liquid, because the protons and neutrons inside it tend to interact only with their nearest neighbours. However, this liquid-drop model ignores the quantum nature of the nucleus. Protons and neutrons move in well defined orbits inside the nucleus, as electrons do inside an atom, and the energy of these orbits depends on the shape of the nucleus.

Ingemar Ragnarsson at the University of Lund in Sweden produced this figure that shows the energy of the orbits (y axis) as a function of the shape of the nucleus. The figure was calculated using a simple harmonic oscillator potential to approximate the energy potential in the nucleus. More than one orbit can have the same energy, which is represented by lines that lie almost on top of each other. Each orbit can hold two nucleons, one spin up and one spin down.

In some parts of the energy diagram there are large gaps between energy levels, for example when the nucleus is spherical (1:1) or “superdeformed” (2:1). If neutrons and protons fill the orbits up to the bottom of such a gap then the configuration is more strongly bound and hence the shape is particularly stable. The numbers indicate how many nucleons can be accommodated by these stable configurations. The gaps persist when more realistic potentials are used in the model, although they then occur for different numbers of nucleons.

Rethinking the nucleus

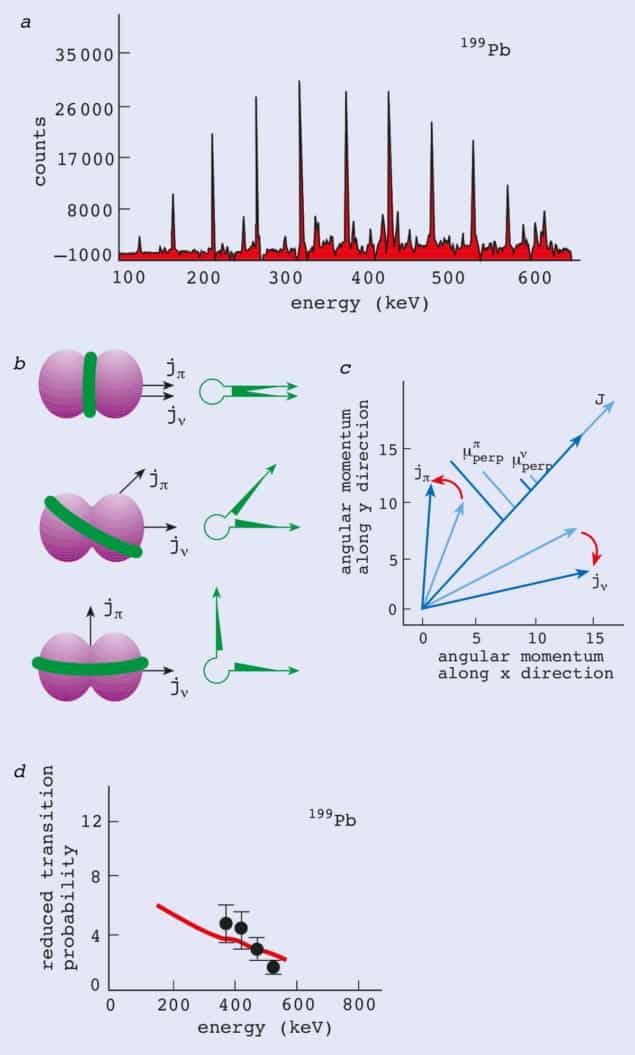
Until recently it was thought that near-spherical nuclei always emitted irregular patterns of gamma-rays. However, in the early 1990s very regular patterns of gamma-rays – and hence possible evidence for rotation – were detected from nuclei that were known to be almost perfect spheres. Working independently, teams from York University in the UK, the Lawrence Berkeley and Lawrence Livermore National Laboratories in the US, and Bonn University in Germany found such patterns in the gamma-ray spectra of lead nuclei with mass numbers of 198 and 199 (figure 4a). Similar examples have since been observed in isotopes of lead with mass numbers of between 191 and 202.

Detailed investigation yielded further surprises. The angular distribution and polarization of the gamma-rays showed that they were not electric quadrupole (E2) in nature but magnetic dipole (M1). Classically, M1 radiation is emitted from a rotating current loop, with the field oscillating at the same frequency as the frequency of rotation. Similar gamma-ray bands have recently been identified in cadmium, indium, tin and antimony nuclei in the mass region around 110, where the nuclei are also near-spherical. These spectra have a pattern that is typical of rotation, which poses an awkward problem: how can we explain these regular patterns of M1 gamma-rays?

In 1993 Stefan Frauendorf of the Centre for Nuclear and Hadron Research in Rossendorf, Germany, suggested that the patterns were due to a new mode of behaviour inside the nucleus. He proposed that most of the angular momentum of the nucleus could be generated by just a few of the protons and neutrons. In the case of lead-199, which has 82 protons and 117 neutrons, it is believed that most of the angular momentum comes from just two protons and three neutrons, with the remaining nucleons being passive observers. (Strictly speaking this angular momentum is carried by protons and “neutron holes”. A neutron hole is the absence of a neutron, similar to an electron hole in a semiconductor.) Since only a few protons and neutrons are involved, there must be a very large angular momentum associated with their orbits.

The coupling of such orbits is governed by the overlap of the wavefunctions that represent the distribution of nucleon density in the nucleus. The protons are thought to have a toroidal (doughnut-shaped) density distribution, whereas the neutron holes have a dumbbell-shaped distribution (figure 4b). Generally, the configuration with the lowest energy is the one where the wavefunctions have the greatest overlap. In lead-199 this occurs when the angular momentum vectors of the protons and neutrons are perpendicular to each other. The alignment of these vectors relative to each other, and of the total angular momentum relative to the magnetic moment of the nucleus, changes during the de-excitation process.

The nuclei are created in highly excited energy and angular momentum states. For a fixed proton and neutron combination, the total angular momentum is at a maximum when the two vectors point in the same direction. During de-excitation these vectors gradually move apart from each other, and hence away from the total angular momentum vector (figure 4c). The separation is gradual in the sense that the total angular momentum decreases in quanta of ħ. As the excess angular momentum and energy is carried away by gamma-rays, the nucleus approaches the minimum-energy configuration in which the two vectors are perpendicular and the overlap between the proton and neutron density wavefunctions is at a maximum. This process has been dubbed the “shears” mechanism because the motion of the proton and neutron angular momentum vectors resembles the opening of a pair of shears. As with superdeformed nuclei, only a small fraction of the nuclei (roughly 1–10%) are created in the shears mode.

A detailed theoretical treatment of the shears mechanism predicts that the “reduced transition probability” (which is inversely proportional to the lifetime of the states in the band) is proportional to the square of the component of the magnetic dipole moment of the nucleus, µ, that is perpendicular to the total angular momentum vector. This component of the dipole moment is small when the angle between the neutron and proton angular momentum vectors is small. As the two vectors open, however, this component becomes larger and the reduced transition probability increases as the total angular momentum decreases. This prediction was recently confirmed by experiments using the Gammasphere array, putting the shears mechanism on a firm experimental footing (figure 4d).

It is easy to see how the orientation of a deformed nucleus (or a dumbbell diatomic molecule) can be specified. But it is not so easy to define an orientation for a nucleus displaying shears behaviour, for which the overall shape is near-spherical. To get a picture of the nucleus, consider the orbits of the few active protons and neutrons involved. Their configuration can be thought of as an anisotropic arrangement of crossed “current” loops embedded in the spherical mass distribution of the nucleus (figure 5a). (Neutrons possess an intrinsic magnetic moment even though they have no overall charge.) An orientation is defined along the total angular momentum vector, J , and the system can rotate about this axis.

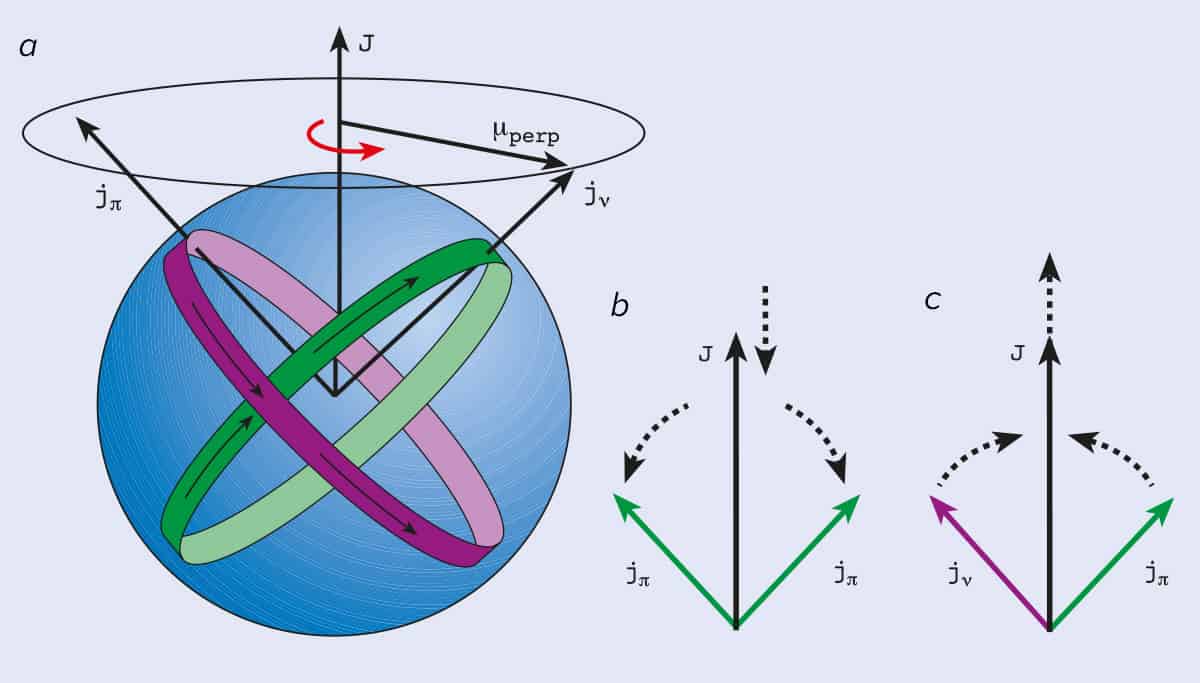
This behaviour has been termed “magnetic rotation” because the rotational sequences arise from the anisotropy of currents in the nucleus, which produce a magnetic moment. The more familiar rotation of deformed nuclei (and molecules) could be called “electric rotation” to reflect the fact that it results from an anisotropy in the charge distribution.

New modes of rotation

What might we expect from future studies of this new phenomenon? The highest priority is to find more examples of the shears mechanism, so that we can study it in a variety of nuclei. In widely separated mass regions the combination of protons and neutrons that form “blades” of the shears will differ. Moreover, the core of the nucleus could assume different shapes. For example, the cases observed in the lead isotopes involve nuclei with small oblate deformations, whereas the examples in the tin region involve slight proflate deformations. And we have yet to find a case of “pure” magnetic rotation in a perfectly spherical nucleus. Another intriguing question is how and when the transition from magnetic to electric rotation occurs?

More exotic versions of the shears mechanism have also been predicted. For instance, both blades of the shears could be formed from the same type of particle (i.e. two neutron blades or two proton blades). However, such a combination could give rise to a large magnetic dipole moment because the individual moments would be equal and opposite (figure 5b). A regular pattern of energy levels would still be formed from the opening shears, but the decay would now occur by weak electric quadrupole transitions. This has been termed “antimagnetic” rotation in analogy with antiferromagnetism.

Another possible shears mode could occur if the blades close with decreasing excitation energy rather than open (figure 5c). There is no physical reason to exclude this possibility, although it would be energetically unfavourable because the angular momentum would increase as the excitation energy decreased. Again the result would be a regular pattern of energy levels. Researchers are currently devising experiments that could reveal these curious modes of behaviour.

The study of rotational motion in nuclear science and other branches of physics is currently an intensely active area of research. For example, rotational-like behaviour has even been observed in the excitation spectra of some families of elementary particles, which offers clues about the behaviour of the constituent quarks. Whatever is found in future studies, one thing is clear – the study of the rotational behaviour of quantum systems will continue to turn up surprises.