Physicists can now routinely exploit the counterintuitive properties of quantum mechanics to transmit, encrypt and even process information. But as Markus Aspelmeyer and Anton Zeilinger describe, the technological advances of quantum information science are now enabling researchers to readdress fundamental puzzles raised by quantum theory

Pure curiosity has been the driving force behind many groundbreaking experiments in physics. This is no better illustrated than in quantum mechanics, initially the physics of the extremely small. Since its beginnings in the 1920s and 1930s, researchers have wanted to observe the counterintuitive properties of quantum mechanics directly in the laboratory. However, because experimental technology was not sufficiently developed at the time, people like Niels Bohr, Albert Einstein, Werner Heisenberg and Erwin Schrödinger relied instead on “gedankenexperiments” (thought experiments) to investigate the quantum physics of individual particles, mainly electrons and photons.
By the 1970s technology had caught up, which produced a “gold rush” of fundamental experiments that continued into the 1990s. These experiments confirmed quantum theory with striking success, and challenged many common-sense assumptions about the physical world. Among these assumptions are “realism” (which, roughly speaking, states that results of measurements reveal features of the world that exist independent of the measurement), “locality” (that the result of measurements here and now do not depend on some action that might be performed a large distance away at exactly the same time), and “non-contextuality” (asserting that results of measurements are independent of the context of the measurement apparatus).
But a big surprise awaited everyone working in this field. The fundamental quantum experiments triggered a completely new field whereby researchers apply phenomena such as superposition, entanglement and randomness to encode, transmit and process information in radically novel schemes. “Quantum information science” is now a booming interdisciplinary field that has brought futuristic-sounding applications such as quantum computers, quantum encryption and quantum teleportation within reach. Furthermore, the technological advances that underpin it have given researchers unprecedented control over individual quantum systems. That control is now fuelling a renaissance in our curiosity of the quantum world by allowing physicists to address new fundamental aspects of quantum mechanics. In turn, this may open up new avenues in quantum information science.
Against intuition
Both fundamental quantum experiments and quantum information science owe much to the arrival of the laser in the 1960s, which provided new and highly efficient ways to prepare individual quantum systems to test the predictions of quantum theory. Indeed, the early development of fundamental quantum-physics experiments went hand in hand with some of the first experimental investigations of quantum optics.
One of the major experimental leaps at that time was the ability to produce “entangled” pairs of photons. In 1935 Schrödinger coined the term “entanglement” to denote pairs of particles that are described only by their joint properties instead of their individual properties — which goes against our experience of the macroscopic world. Shortly beforehand, Einstein, Boris Podolsky and Nathan Rosen (collectively known as EPR) used a gedankenexperiment to argue that if entanglement exists, then the quantum-mechanical description of physical reality must be incomplete. Einstein did not like the idea that the quantum state of one entangled particle could change instantly when a measurement is made on the other particle. Calling it “spooky” action at a distance, he hoped for a more complete physical theory of the very small that did not exhibit such strange features (see “The power of entanglement” by Harald Weinfurter Physics World January 2005 pp47–51).
This lay at the heart of a famous debate between Einstein and Bohr about whether physics describes nature “as it really is”, as was Einstein’s view, or whether it describes “what we can say about nature”, as Bohr believed. Until the 1960s these questions were merely philosophical in nature. But in 1964, the Northern Irish physicist John Bell realized that experiments on entangled particles could provide a test of whether there is a more complete description of the world beyond quantum theory. EPR believed that such a theory exists.
Bell based his argument on two assumptions made by EPR that are directly contradicted by the properties of entangled particles. The first is locality, which states that the results of measurements performed on one particle must be independent of whatever is done at the same time to its entangled partner located at an arbitrary distance away. The second is realism, which states that the outcome of a measurement on one of the particles reflects properties that the particle carried prior to and independent of the measurement. Bell showed that a particular combination of measurements performed on identically prepared pairs of particles would produce a numerical bound (today called a Bell’s inequality) that is satisfied by all physical theories that obey these two assumptions. He also showed, however, that this bound is violated by the predictions of quantum physics for entangled particle pairs (Physics 1 195).
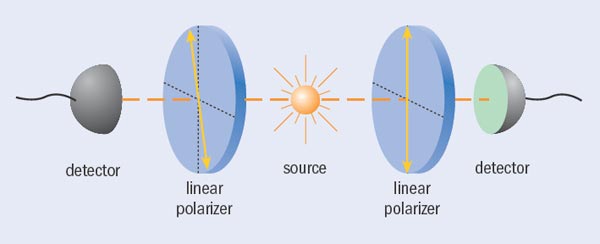
Take, for example, the polarization of photons. An individual photon may be polarized along a specific direction, say the horizontal, and we can measure this polarization by passing the photon through a horizontally oriented polarizer. A click in a photon detector placed behind it indicates a successful measurement and shows that the photon is horizontally polarized; no click means that the photon is polarized along the vertical direction. In the case of an entangled pair of photons, however, the individual photons turn out not to carry any specific polarization before they are measured! Measuring the horizontal polarization of one of the photons will always give a random result, thus making it equally likely to find an individual photon horizontally or vertically polarized. Yet performing the same measurement on the other photon of the entangled pair (assuming a specific type of entangled state) will show both photons to be polarized along the same direction. This is true for all measurement directions and is independent of the spatial separation of the particles.
Bell’s inequality opened up the possibility of testing specific underlying assumptions of physical theories — an effort rightfully referred to by Abner Shimony of Boston University as “experimental metaphysics”. In such Bell experiments, two distant observers measure the polarization of entangled particles along different directions and calculate the correlations between them. Because the quantum correlations between independent polarization measurements on entangled particles can be much stronger than is allowed by any local realistic theory, Bell’s inequality will be violated.
Quantum loopholes
The first such test was performed using entangled photons in 1972 by Stuart Freedman and John Clauser of the University of California at Berkeley; Bell’s inequality was violated and the predictions of quantum theory were confirmed (Phys. Rev. Lett. 28 938). But from early on there existed some loopholes that meant researchers could not exclude all possible “local realistic” models as explanations for the observed correlations. For example, it could be that the particles detected are not a fair sample of all particles emitted by the source (the so-called detection loophole) or that the various elements of the experiment may still be causally connected (the locality loophole). In order to close these loopholes, more stringent experimental conditions had to be fulfilled.
In 1982 Alain Aspect and colleagues at the Université Paris-Sud in Orsay, France, carried out a series of pioneering experiments that were very close to Bell’s original proposal. The team implemented a two-channel detection scheme to avoid making assumptions about photons that did not pass through the polarizer (Phys. Rev. Lett. 49 91), and the researchers also periodically — and thus deterministically — varied the orientation of the polarizers after the photons were emitted from the source (Phys. Rev. Lett. 49 1804). Even under these more stringent conditions, Bell’s inequality was violated in both cases, thus significantly narrowing the chances of local-realistic explanations of quantum entanglement.
In 1998 one of the present authors (AZ) and colleagues, then at the University of Innsbruck, closed the locality loophole by using two fully independent quantum random-number generators to set the directions of the photon measurements. This meant that the direction along which the polarization of each photon was measured was decided at the last instant, such that no signal (which by necessity has to travel slower than the speed of light) would be able to transfer information to the other side before that photon was registered (Phys. Rev. Lett. 81 5039). Bell’s inequality was violated.
Then in 2004, David Wineland and co-workers at the National Institute of Standards and Technology (NIST) in Colorado, US, set out to close the detection loophole by using detectors with perfect efficiency in an experiment involving entangled beryllium ions (Nature 409 791). Once again, Bell’s inequality was violated. Indeed, all results to date suggest that no local-realistic theory can explain quantum entanglement.
But the ultimate test of Bell’s theorem is still missing: a single experiment that closes all the loopholes at once. It is very unlikely that such an experiment will disagree with the prediction of quantum mechanics, since this would imply that nature makes use of both the detection loophole in the Innsbruck experiment and of the locality loophole in the NIST experiment. Nevertheless, nature could be vicious, and such an experiment is desirable if we are to finally close the book on local realism.
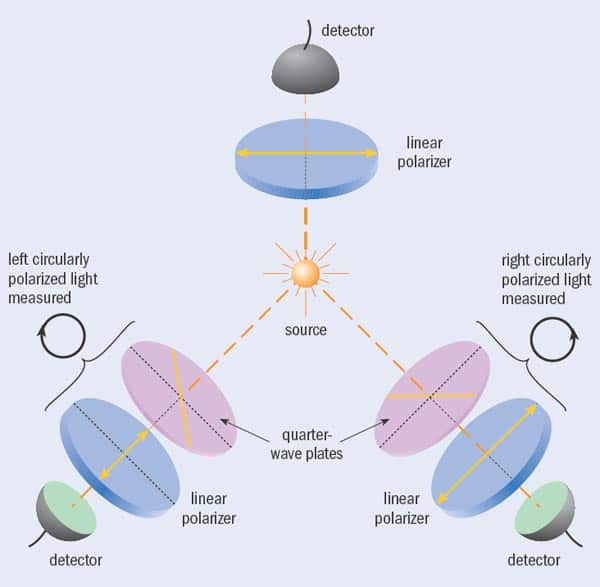
In 1987 Daniel Greenberger of the New York City College, Michael Horne of Stonehill College and AZ (collectively GHZ) realized that the entanglement of three or more particles would provide an even stronger constraint on local realism than two-particle entanglement (Am. J. Phys. 58 1131). While two entangled particles are at variance with local realism only in their statistical properties, which is the essence of Bell’s theorem, three entangled particles can produce an immediate conflict in a single measurement result because measurements on two of the particles allow us to predict with certainty the property of the third particle.
The first experiments on three entangled photons were performed in late 1999 by AZ and co-workers, and they revealed a striking accordance with quantum theory (Nature 403 515). So far, all tests of both Bell’s inequalities and on three entangled particles (known as GHZ experiments) (see “GHZ experiments”) confirm the predictions of quantum theory, and hence are in conflict with the joint assumption of locality and realism as underlying working hypotheses for any physical theory that wants to explain the features of entangled particles.
Quantum information science
The many beautiful experiments performed during the early days of quantum optics prompted renewed interest in the basic concepts of quantum physics. Evidence for this can be seen, for example, in the number of citations received by the EPR paper, which argued that entanglement renders the quantum-mechanical description of physical reality incomplete. The paper was cited only about 40 times between its publication in 1935 and 1965, just after Bell developed his inequalities. Yet today it has more than 4000 citations, with an average of 200 per year since 2002. Part of the reason for this rise is that researchers from many different fields have begun to realize the dramatic consequences of using entanglement and other quantum concepts to encode, transmit and process information.
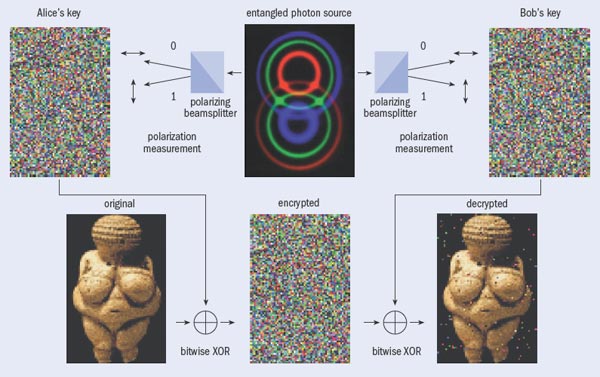
Take quantum cryptography, which applies randomness, superposition and, in one scheme proposed by Artur Ekert of Oxford University in the UK, two-particle entanglement to transmit information such that its security against eavesdropping is guaranteed by physical law (see “Entanglement-based quantum cryptography”). This application of quantum information science has already left the laboratory environment. In 2004, for instance, AZ and co-workers at the University of Vienna transferred money securely between an Austrian bank and Vienna City Hall using pairs of entangled photons that were generated by a laser in a nonlinear optical process and distributed via optical fibres. More recently, two international collaborations were able to distribute entangled photons over a distance of 144 km between La Palma and Tenerife, including a demonstration of quantum cryptography, and earlier this year even showed that such links could be established in space by bouncing laser pulses attenuated to the single-photon level off a satellite back to a receiving station on Earth (Physics World May p4). Commercial quantum-encryption products based on attenuated laser pulses are already on the market (see “Key to the quantum industry”), and the challenge now is to achieve higher bit rates and to bridge larger distances.
In a similar manner, the road leading to the GHZ experiments opened up the huge field of multiparticle entanglement, which has applications in, among other things, quantum metrology. For example, greater uncertainty in the number of entangled photons in an interferometer leads to less uncertainty in their phases, thereby resulting in better measurement accuracy compared with a similar experiment using the same number of non-entangled photons.
Multiparticle entanglement is also essential for quantum computing. Quantum computing exploits fundamental quantum phenomena to allow calculations to be performed with unprecedented speed — perhaps even solving problems that are too complex for conventional computers, such as factoring large prime numbers or enabling fast database searches. The key idea behind quantum computing is to encode and process information in physical systems following the rules of quantum mechanics. Much current research is therefore devoted to finding reliable quantum bits or “qubits” that can be linked together to form registers and logical gates analogous to those in conventional computers, which would then allow full quantum algorithms to be implemented.

In 2001, however, Robert Raussendorf and Hans Briegel, then at the University of Munich in Germany, suggested an alternative route for quantum computation based on a highly entangled multiparticle “cluster state” (Phys. Rev. Lett. 86 5188). In this scheme, called “one-way” quantum computing, a computation is performed by measuring the individual particles of the entangled cluster state in a specific sequence that is defined by the particular calculation to be performed. The individual particles that have been measured are no longer entangled with the other particles and are therefore not available for further computation. But those that remain within the cluster state after each measurement end up in a specific state depending on which measurement was performed. As the measurement outcome of any individual entangled particle is completely random, different states result for the remaining particles after each measurement. But only in one specific case is the remaining state the correct one. Raussendorf and Briegel’s key idea was to eliminate that randomness by making the specific sequence of measurements depend on the earlier results. The whole scheme therefore represents a deterministic quantum computer, in which the remaining particles at the end of all measurements carry the result of the computation.
In 2005 the present authors and colleagues at Vienna demonstrated the principle of one-way quantum computing (see “One-way quantum computation”) and even a simple search algorithm using a four-photon entangled state (Nature 434 169). Then in 2007, Jian-Wei Pan of the University of Science and Technology of China in Hefei and coworkers implemented a similar scheme involving six photons. A distinct advantage of a photonic one-way computer is its unprecedented speed, with the time from the measurement of one photon to the next, i.e. a computational cycle, taking no more than 100 ns.
Foundational questions
The technology developed in the last 20 years to make quantum information processing and communication a reality has given researchers unprecedented control over individual quantum systems. For example, it is now clear that all-photonic quantum computing is possible but that it requires efficient and highly pure single-photon and entangled-photon sources, plus the ability to reliably manipulate the quantum states of photons or other quantum systems in a matter of nanoseconds. The tools required for this and other developments are being constantly improved, which is itself opening up completely new ways to explore the profound questions raised by quantum theory.
One such question concerns once again the notions of locality and realism. The whole body of Bell and GHZ experiments performed over the years suggests that at least one of these two assumptions is inadequate to describe the physical world (at least as long as entangled states are involved). But Bell’s theorem does not allow us to say which one of the two should be abandoned.
In 2003 Anthony Leggett of the University of Illinois at Urbana-Champaign in the US provided a partial answer by presenting a new incompatibility theorem very much in the spirit of Bell’s theory but with a different set of assumptions (Found. Phys. 33 1469). His idea was to drop the assumption of locality and to ask if, in such a situation, a plausible concept of realism — namely to assign a fixed polarization as a “real” property of each particle in an entangled pair — is sufficient to fully reproduce quantum theory. Intuitively, one might expect that properly chosen non-local influences can produce arbitrary correlations. After all, if you allow your measurement outcome to depend on everything that goes on in the whole universe (including at the location of the second measurement apparatus), then why should you expect a restriction on such correlations?
For the specific case of a pair of polarization-entangled photons, the class of non-local realistic theories Leggett sets out to test fulfils the following assumptions: each particle of a pair is emitted from the source with a well-defined polarization; and non-local influences are present such that each individual measurement outcome may depend on any parameter at an arbitrary distance from the measurement. The predictions of such theories violate the original Bell inequalities due to the allowed non-local influence, so it is natural to ask whether they are able to reproduce all predictions of quantum theory.
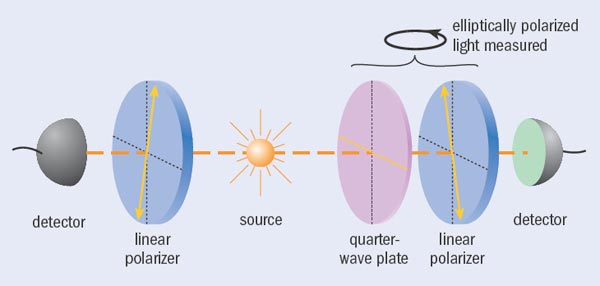
Leggett showed that this is not the case. Analogous to Bell, he derived a set of inequalities for certain measurements on two entangled particles that are fulfilled by all theories based on these specific non-local realistic assumptions but which are violated by quantum-theoretical predictions. Testing Leggett’s inequalities is more challenging than testing Bell’s inequalities because they require measurements of both linear and elliptic polarization, and much higher-quality entanglement. But in 2007, thanks to the tremendous progress made with entangled-photon sources, the present authors and colleagues at Vienna were able to test a Leggett inequality experimentally by measuring correlations between linear and elliptical polarizations of entangled photons (Nature 446 871).
The experiment confirmed the predictions of quantum theory and thereby ruled out a broad class of non-local realistic theories as a conceptual basis for quantum phenomena. Similar to the evolution of Bell experiments, more rigorous Leggett-type experiments quickly followed. For example, independent experiments performed in 2007 by the Vienna team (Phys. Rev. Lett. 99 210406) and by researchers at the University of Geneva and the National University of Singapore (Phys. Rev. Lett. 99 210407) confirmed a violation of a Leggett inequality under more relaxed assumptions, thereby expanding the class of forbidden non-local realistic models. Two things are clear from these experiments. First, it is insufficient to give up completely the notion of locality. Second, one has to abandon at least the notion of naïve realism that particles have certain properties (in our case polarization) that are independent of any observation.
Macroscopic limits
The close interplay between quantum information science and fundamental curiosity has also been demonstrated by some fascinating experiments that involve more massive particles. According to quantum theory, there is no intrinsic upper limit on size or complexity of a physical system above which quantum effects no longer occur. This is at the heart of Schrödinger’s famous cat paradox, which ridicules the situation by suggesting an experiment whereby someone could prepare a cat that is in a superposition of being alive and dead. One particularly interesting case is that of “matter–wave” interference.
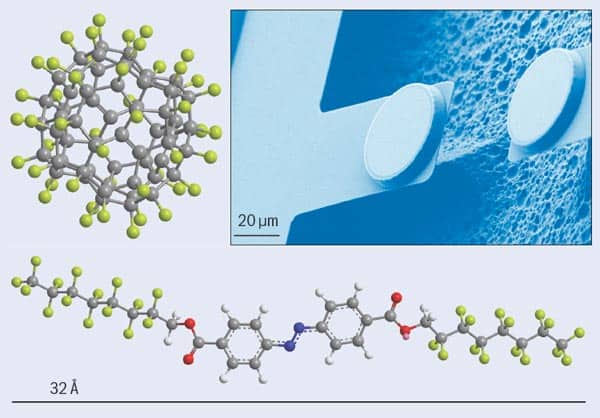
Electrons, neutrons and atoms have been shown to exhibit interference effects when passing through a double-slit, thus proving that these massive systems neither passed through only one or the other slit. Similar behaviour was observed more recently in 1999 by AZ and colleagues at Vienna for relatively large carbon-60 and carbon-70 fullerene molecules (Nature 401 680), and ongoing research has demonstrated interference with even heavier and larger systems (see “Macroscopic quantum experiments”). One of the main goals of this research is to realize quantum interference for small viruses or maybe even nanobacteria.
Very recently the ability to cool nanomechanical devices to very low temperatures has opened up a new avenue to test systems containing up to 1020 atoms. One fascinating goal of experiments that probe the quantum regime of mechanical cantilevers is to demonstrate entanglement between a microscopic system such as a photon and a mechanical system — or even between two mechanical systems.
While the underlying motivation for studying macroscopic quantum systems is pure curiosity, the research touches on important questions for quantum information science. This is because increasingly large or complex quantum systems suffer from interactions with their environment, which is as important for macromolecules and cantilevers as it is for the large registers of a quantum computer.
One consequence of this interaction with the outside world is “decoherence”, whereby the system effectively becomes entangled with the environment and therefore loses its individual quantum state. As a result, measurements of that system are no longer able to reveal any quantum signature. Finding ways to avoid decoherence is thus a hot topic both in macroscopic quantum experiments and in quantum information science. With fullerene molecules, for instance, the effect of decoherence was studied in great detail in 2004 by coupling them to the outside environment in different, tuneable ways (Nature 427 711). From an experimental point of view, we see no reason to expect that decoherence cannot be overcome for systems much more macroscopic than is presently feasible in the laboratory.
Quantum curiosity
Quantum physics and the information science that it has inspired emerge as two sides of the same coin: as inspiration for conceptually new approaches to applications on the one side; and as an enabling toolbox for new fundamental questions on the other. It has often happened that new technologies raise questions that have not been asked before, simply because people could not imagine what has become possible in the laboratory.
One such case may be our increasing ability to manipulate complex quantum systems that live in high-dimensional Hilbert space — the mathematical space in which quantum states are described. Most of the known foundational questions in quantum theory have hitherto made use only of relatively simple systems, but larger Hilbert-space dimensions may add qualitatively new features to the interpretation of quantum physics. We are convinced that many surprises await us there.
We expect that future theoretical and experimental developments will shine more light on which of the counterintuitive features of quantum theory are really indispensable in our description of the physical world. In doing so, we expect to gain greater insight into the underlying fundamental question of what reality is and how to describe it. The close connection between basic curiosity of the quantum world and its application in information science may even lead to ideas for physics beyond quantum mechanics.
At a Glance: A quantum renaissance
- Quantum mechanics challenges intuitive notions about reality, such as whether the property of a particle exists before a measurement is performed on it
- Entanglement is one of the most perplexing aspects of quantum theory; it implies that measurement results on two particles are intimately connected to one another instantaneously no matter how far apart they are
- Since the 1970s, experiments have shown repeatedly that quantum theory is correct, but researchers are still devising measurements in order to find out what quantum mechanics tells us about physical reality
- These tests have sparked a new field called quantum information science, in which entanglement and other quantum phenomena are used in to encrypt, transmit and process information in radically new ways
- The increased level of control over individual quantum systems that has driven quantum information science is now enabling physicists to tackle once again the fundamental puzzles raised by quantum theory
More about: A quantum renaissance
M Arndt, K Hornberger and A Zeilinger 2005 Probing the limits of the quantum world Physics World March pp35–40
D Bouwmeester et al. (ed) 1999 The Physics of Quantum Information (Springer, Heidelberg)
A Steinberg et al. 1996 Quantum optical tests of the foundations of physics The American Institute of Physics Atomic, Molecular, and Optical Physics Handbook (ed) G W F Drake (AIP Press)
A Zeilinger et al. 2005 Happy centenary, photon Nature 433 239



