In 1967 the Russian physicist Victor Veselago predicted the existence of a material with a negative index of refraction, which he termed “left-handed.” He concluded that in the presence of such a negative-index material nearly all known wave propagation and optical phenomena would be substantially altered, although negative-index materials were not known to exist at the time.

More than 30 years later, negative-index phenomena are finally being investigated. The reason for the intense activity in recent years is the emergence of a new class of artificially structured materials called metamaterials. The electromagnetic properties of metamaterials are governed by elements that are patterned on a macroscopic scale and that take the place of atoms or molecules in naturally occurring materials. They can therefore be engineered so that they have a much wider range of electromagnetic responses, including the elusive negative index.

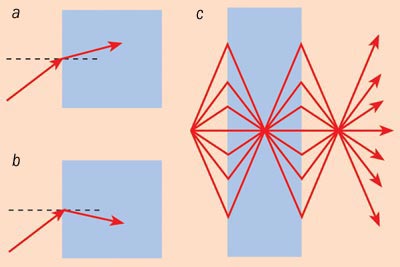
Veselago predicted that certain optical phenomena would be completely reversed in a negative-index material. Perhaps the most striking of these is refraction, in which an electromagnetic wave is bent when it passes through the interface between two different materials. Normally, the wave will emerge on the opposite side of the line that runs perpendicular to the interface (the “surface normal”). However, if one material has a positive index and the other has a negative index, the wave will emerge on the same side of the surface normal as the incident wave.

Focused refraction

Figure 1

Many groups have demonstrated negative refraction in metamaterials, confirming Veselago’s early prediction (see “The reality of negative refraction”). In particular, this initial work has demonstrated the enormous potential for a new generation of lenses, which function, of course, by refracting the rays of incident waves. Negative refraction implies that a converging lens made from negative-index material should have a concave surface rather than a convex one. While this change may not seem profound, a negative-index lens has remarkably different properties from a positive-index lens, stemming from an inherent asymmetry between the two. For instance, air or a vacuum has a refractive index of n = +1, so a piece of material with refractive index n = +1 does not refract rays, and thus cannot form a lens, whereas a material with n = -1 refracts rays strongly.

Recently, Claudio Parazzoli, Robert Greegor and colleagues in the Phantom Works division of Boeing have exploited this asymmetry to produce a plano-concave metamaterial lens with a negative refractive index that has unique advantages over equivalent positive-index lenses (Appl. Phys. Lett. at press). What is intriguing, however, is that the n = -1 material can form a lens without curved surfaces, as hypothesized by Veselago. The trajectory of each ray that leaves a nearby source is exactly reversed as it enters an n = -1 slab, such that all the rays are focused at the centre of the material and then once again outside it (figure 1c). The question is, can a negative-index lens produce an image that has a higher resolution than that of a conventional lens?

Perfect prediction

Unlike the source depicted in figure 1c, a real electromagnetic source has what are called near-field components in addition to the far-field, or propagating, components shown. These quasistatic field components decay with distance from the source, which means that the final image always contains less information than is contained in the source. This diffraction limit – which is associated with all positive-index optical components – means that the best resolution that is possible corresponds to about half of the incident wavelength of the light that is used to produce the image.

In 2000 John Pendry of Imperial College in the UK considered the negative-index planar lens in more detail and reached a remarkable conclusion. He found that in addition to refocusing the far-field propagating components, such a lens could also refocus the near-field components. In order to achieve this, however, the n = -1 lens would need to amplify the near-field components, causing them to grow exponentially within the slab. In principle, such a lens would provide perfect image reconstruction, prompting Pendry to dub the n = -1 slab a “perfect lens”.

Pendry’s prediction proved unsettling for many, and sparked a vigorous debate (see Physics World August 2002 pp8–9). Several researchers drew attention to apparent conflicts with known physical limitations, such as energy conservation or the uncertainty principle. As remarkable as Pendry’s prediction might seem, however, the prospect of a lens that can beat the diffraction limit has survived these challenges.

Negative circuits

As with most negative-index phenomena, the key to producing the near-field refocusing effect is to develop the metamaterial. Intrigued by the prospect of beating the diffraction limit, Anthony Grbic and George Eleftheriades of the University of Toronto have formed an analogous metamaterial based on electrical transmission lines. A standard transmission line consists of repeated cells that contain inductors in series and capacitors in parallel, so that it can support propagating electromagnetic waves with the same dispersion characteristics (i.e. frequency versus wavelength) as a positive-index material.

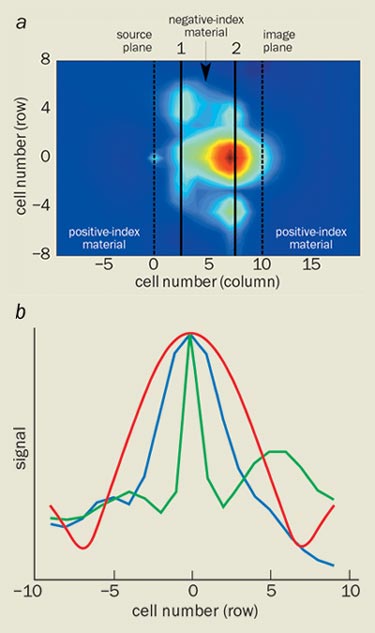
By reversing the positions of the inductors and the capacitors, the transmission line becomes the analogue of a negative-index medium. Grbic and Eleftheriades created a circuit equivalent to a perfect lens by placing a rectangular negative-index transmission-line between two positive-index transmission lines. With this metamaterial, they have managed to refocus the near-field components of a 1.057 GHz wave (Phys. Rev. Lett. at press).

To demonstrate this, the Toronto team placed an electromagnetic antenna (the source) on one side of the negative-index region and mapped the electromagnetic fields both within the slab and on the other side (the image plane). They found that the recovered image does indeed have a resolution that is better than that which the diffraction limit implies – in agreement with Pendry’s prediction (figure 2). However, the image is still broader than the source, which means it is not perfect. This is due to material losses in the transmission-line metamaterial, which place a limit on how well the near-fields can be recovered; build a better metamaterial, and the resolution will improve.

This latest round of experiments provides strong evidence that negative-index metamaterials have an important future in imaging. Negative-index lenses offer a new degree of flexibility that could lead to more compact lenses with reduced aberration. Furthermore, the remarkable phenomenon of near-field focusing demonstrated by Grbic and Eleftheriades implies that the diffraction limit – which is the most fundamental limitation to image resolution – may, in fact, be circumvented by negative-index materials.

While the results reported so far have demonstrated negative refraction at microwave frequencies, recent experiments and theoretical work suggest that photonic crystals may enable these wonderful effects to be demonstrated at visible wavelengths.