Quantum computers can now simulate much larger quantum systems than was previously thought possible thanks to algorithms developed by researchers in the UK and Germany. The new algorithms divide up quantum computational resources according to which parts of the simulation require them most, making it possible to extract information about a large quantum system from many smaller, more manageable calculations – in effect, running the simulation in parallel. The result should boost the capabilities of the current generation of so-called noisy intermediate scale quantum (NISQ) computers, which lack the computational resources required to perform useful algorithms in materials science or drug discovery, both of which depend heavily on a deep understanding of quantum effects.
Quantum computers promise to perform complex calculations today’s classical supercomputers cannot. A bottleneck for achieving such a “quantum advantage” is that it is very difficult to engineer a large, error-free quantum computer. While upgrading the quantum technologies themselves might seem like the obvious solution, it is also possible to improve the algorithms that run on such computers – for example, by changing the way thinformation.
Representing quantum states efficiently
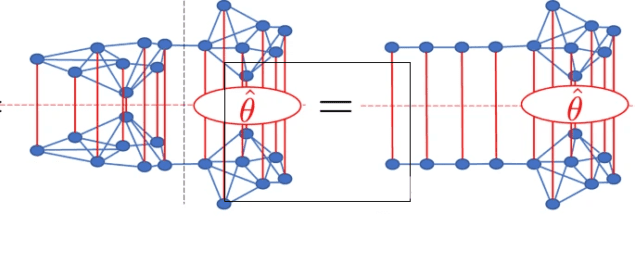
In the latest work, published in npj Quantum Information, researchers at University College London (UCL), the Technical University of Munich, King’s College London and the biotech company Kuano (formerly a quantum start-up called GTN) took inspiration from a set of mathematical tools known as tensor networks. Tensor network methods were originally developed to simulate quantum systems classically, and their chief selling point is that they are very efficient at storing the information needed to describe certain classes of large quantum states. They achieve this efficiency by focusing on the quantum effects that are most important (like entanglement), purposefully allocating fewer computational resources to those that are not.
By translating these methods to quantum computing algorithms, the team showed that similar advantages apply even when the processors are quantum. The approach allows computational resources to be divided, so that the separate components of the algorithms can be run in parallel on different quantum processors and their results combined at the end. This may be useful in simulating large molecules that have complicated quantum interactions only in certain regions. These regions could each be assigned a processor, with the simpler interactions between them relegated to a separate computation of their own.
Extra advantages
While the team’s approach emulates what tensor networks already do on classical computers, running such computations on quantum computers has potential advantages that could never be attained classically. This is largely because of something called the bond dimension, which is a way of modelling the amount of entanglement in a quantum state. For highly entangled quantum systems, this bond dimension becomes large and makes the computation inefficient. On a quantum computer, however, the resources required may be greatly reduced. “Tensor networks are the very best way to simulate many quantum systems on classical computers,” says Andrew Green, a condensed-matter physicist at UCL and a co-author of the study. “We expect that translating them to quantum computers will unlock a quantum advantage.”
Quantum adiabatic and quantum circuit algorithms are equivalent, say physicists
To test their approach, Green and colleagues simulated an Ising spin chain, which is a large one-dimensional quantum system that is often used to model interesting optimization problems. The scale of this system is far beyond what has previously been achieved on a quantum computer, indicating that it is possible to extract useful information about large quantum systems from many small-scale calculations on current quantum computing hardware.
According to the researchers, a possible follow-up would be to develop algorithms to simulate two- or three-dimensional quantum systems, as well as systems that may be far less ordered than those that scientists have investigated so far. They hope that while such systems – like those with complicated forms of entanglement – are proving challenging for classical tensor network approaches, translating them to quantum computers may finally lead to a breakthrough.