Experiment confirms that information cannot be transmitted faster than the speed of light
Ever since Einstein stated that nothing can travel faster than light, physicists have delighted in finding exceptions. One after another, observations of such “superluminal” propagation have been made. However, while some image or pattern- such as the motion of a spotlight projected on a distant wall – might have appeared to travel faster than light, it seemed that there was no way to use the superluminal effect to transmit energy or information.
In recent years, the superluminal propagation of light pulses through certain media has led to renewed controversy. In 1995, for example, Günther Nimtz of the University of Cologne encoded Mozart’s 40th Symphony on a microwave beam, which he claimed to have transmitted at a speed faster than light. Others maintain that such a violation of Einstein’s speed limit would wreak havoc on our most fundamental ideas about causality, allowing an effect to precede its cause. Relativity teaches us that sending a signal faster than light would be equivalent to sending it backwards in time.
Now an experiment by Michael Stenner and Daniel Gauthier at Duke University in North Carolina and Mark Neifeld at the University of Arizona promises to shed fresh light on this century-old conundrum. The Duke-Arizona team has attempted to directly measure the “speed of information” by sending a message through a superluminal medium (M Stenner et al. 2003 Nature 425 695). However, the work could merely fan the flames of the dispute over faster-than-light propagation.
The speed of light
Special relativity tells us that no matter how much kinetic energy a massive object gains, its speed will never exceed the speed of light in a vacuum, c. This, at least, is generally accepted. However, the issue for light – which is an electromagnetic wave composed of massless photons – has never been quite as clear-cut. Special relativity says that massless particles always travel exactly at c, but one of the first things we are taught about light is that it travels slower in glass or water than it does in a vacuum.
This delay is due to the absorption and re-emission of photons by particles in the medium. When light hits an atom, the electrons begin vibrating at the optical frequency, and the electromagnetic fields that they re-radiate interfere with the original fields. Whether this interference delays or advances the phase of the waves depends on the properties of the atom and the frequency of the wave.
The fact that light might travel faster than it does in a vacuum caused great bewilderment at the beginning of the 20th century. But the issue was eventually clarified by Arnold Sommerfeld and Léon Brillouin, who showed that the “phase velocity” – the speed of the individual ripples on an idealized wave that extends to infinity in both directions – does not directly describe the motion of the energy in a light pulse. Instead, Sommerfeld and Brillouin realized that the propagation of a photon should be described by the speed at which the peak of localized packets of ripples moves – the “group velocity”. Even when the phase velocity is faster than light, the group velocity should be slower.
Despite this careful redefinition of the velocity of a wave, there are, in fact, still exotic situations where the group velocity can exceed c. However, these situations are characterized by a great deal of absorption and distortion, which led Sommerfeld and Brillouin to argue that the group velocity itself loses any meaning in such regions. They showed that any abrupt change in the pulse shape – which the person receiving the signal would not expect, and which would therefore carry new information – would travel not at this superluminal group velocity but only at c.
The speed of information
Experiments in the 1980s, however, showed that it was possible for the peak of a wave packet to arrive sooner than it would had it travelled at c. Most researchers agreed that the peaks of such smooth, predictable pulses carried no new information, since one could foresee the arrival of the peak from the shape of the earlier portion of the pulse. The modern version of Einstein’s law that no signal can travel faster than light was therefore left intact. Some researchers, on the other hand, pointed out that these “superluminal” pulses could well be used to trigger a practical detection system earlier than pulses that had travelled at c.
One obstacle to resolving the issue was that all known examples of superluminality involved the loss of most of the incident pulse, either through absorption or reflection. This loss degrades the quality of any signal, leaving open the argument that it could still take longer to accumulate information than in the case of slower, but lossless, transmission through the vacuum.
However, 10 years ago Raymond Chiao of the University of California at Berkeley proposed that under the right conditions an optical pulse might pass through a transparent (lossless) medium faster than light. Together, we suggested an experiment in which this could be observed. The idea was to pump a sample of atoms into an inverted state in which their optical properties are essentially opposite to those in normal matter, and then to tune the signal probe to a particular frequency that allowed it to propagate superluminally.
In 2000 Lijun Wang and co-workers at NEC in Princeton demonstrated this effect, proving that a pulse peak could exit a small vapour cell even before it should have had time to enter (see “No thing goes faster than light” and “Taming light with cold atoms”). This rekindled the embers of controversy, and much theoretical work has followed. However, until now no experiment has come any closer to closing the book on this issue.
The work of Stenner and colleagues extends the NEC work in two ways. First the researchers devised an improved way to pump a sample of potassium vapour into the special superluminal state, which allowed them to increase the relative size of the effect by a factor of five. Instead of an advance of only 1/50 of the original pulse width, as Wang and co-workers had achieved, their pulse leaped an astounding 1/10 of a pulse width ahead of one travelling at c.
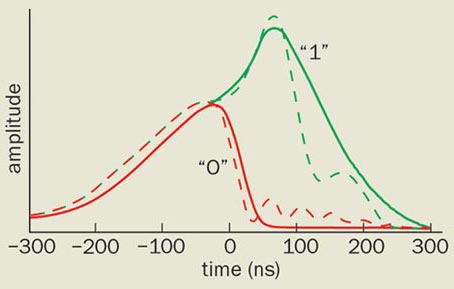
Second, not content to work with infinitely smooth, predictable pulses, the researchers encoded a realistic “signal” on top of their light beams (see figure). This signal can represent either a “1” or a “0”, and the goal is to find the earliest moment at which a receiver would be able to determine whether a “0” or a “1” had been sent. Stenner and co-workers found that although the smooth pulse arrives noticeably earlier through the superluminal medium, the instant at which the “1s” and “0s” begin to differ does not seem to be accelerated. In fact, carrying out a very careful analysis of signal and noise, and eliminating nearly all spurious delays that the equipment itself might introduce, the team found that “new” information actually arrives somewhat slower than light.
New information
This result will be welcomed by mainstream physicists, who believe that Einstein’s speed limit will always be respected. But it is worth pointing out that in this experiment, as in any real-world situation, the detection of information has to be defined statistically in terms of how long it takes to reach a certain level of confidence about the content of the message. In reality, there is always some delay between the decision to send a message and the point at which the first photon leaves the transmitter. Similarly, it takes a finite time after the arrival of this first photon before any level of confidence can be achieved.
It is therefore easy to mistake a reduction in these latency times for true faster-than-light propagation. For example, a system that filters out some of the noise would make it easier to extract the message quickly. While the current experiment has done an excellent job of eliminating spurious effects, it would be easy to construct similar experiments that erroneously indicate superluminal information transfer. Furthermore, one could argue that such information transfer could have occurred but still be masked from view by mere technical noise.
Perhaps more important is the continuing uncertainty about how to truly pin down, even in theory, where this “new information” resides. Clearly, a signal cannot be spread out over all of history in a perfectly smooth pulse. On the other hand, truly discontinuous pulses are never observed in the real world and they are unpalatable even in theory. While theorists focus on geometric points where something unpredictable happens, experimentalists counter that no energy is contained in an idealized point, and that no information can be obtained until at least one photon is detected. Experiments like this force us – in this information-dominated age – to come to terms with the fact that we still do not truly know how to describe a task as simple as saying “yes” or “no”.