Once thought to offer imaging at unlimited resolution beyond that permitted by diffraction, superlenses never quite worked in practice. Now, physicists have a host of other ideas to make perfect images, but can these concepts succeed where superlenses failed? Jon Cartwright reports
Ernst Abbe, one of the 19th-century pioneers of modern optics, has a concrete memorial sitting in the leafy grounds of the Friedrich Schiller University of Jena, Germany, engraved with a formula. Put simply, it describes a fundamental limit of all lenses: they cannot see everything. No matter how finely you grind and polish a lens, diffraction – the natural spreading of light waves – will always blur the smallest details.
Of course, theories should never be set in stone. At the turn of this century, physicists began to explore “superlenses” that could see past Abbe’s diffraction limit – that is, they could see features smaller than about half a wavelength of the light being used. Based on thin slabs of metal, these superlenses could bend light in unheard-of ways, counteracting diffraction so that an object’s features could be resolved into a perfect image. But there were problems: the lenses only worked if they were placed right next to an object and, even then, they were so lossy that their images were next to useless. Superlenses were not so super after all.
For many, that was a great shame. Biologists had been looking forward to imaging the tiniest parts of organisms in real time, which is almost impossible with current microscopy techniques. Perfect imaging could also have rebooted the computer-chip industry, allowing circuits and components to be etched smaller and more complex than before. Although other techniques exist that can see features smaller than half a wavelength – near-field scanning optical microscopy is one – they produce images by scanning a surface, which takes time. Only perfect imaging promised the ability to image objects at any resolution in a single snapshot.
Given the poor results of superlenses, some physicists have tried rehashing the blueprint in the hope that it can still offer practical applications. Others, however, have ditched the concept altogether, instead trying completely different approaches. These new approaches are in their nascent stages – most have not actually imaged anything, but only resolved point sources. Still, they are under high expectations, and could allow us to see more clearly than ever before.
Going negative
The superlens was a bold idea. First proposed in 2000 by theorist John Pendry of Imperial College, London, it hinges – as do all conventional lenses – on a property known as the refractive index. This describes the degree by which light bends as it enters a material – think how a stick dipped in water appears to bend towards the surface. As you would expect, a greater refractive index results in stronger bending. But Pendry’s insight came when he considered something radical: a negative refractive index.
To understand negative refraction, it is best to accept a little help from Albert Einstein. His general theory of relativity shows that very massive objects, such as stars or black holes, distort the underlying fabric of the universe – space–time – thereby bending the passage of light. Since refraction also bends light, one can picture it distorting an equivalent fabric – a virtual “optical space”. Negative refraction involves distorting optical space so much that it folds back on itself: a stick dipped in a negative-index substance would appear to bend the opposite way to usual.
Applying negative refraction to imaging, Pendry discovered a remarkable effect. Light rays usually defocus as they leave an object, but Pendry showed theoretically that negative refraction should cause these light rays to reconverge, creating an image of the object in perfect detail. Subsequent experiments proved him right, with superlenses achieving image resolutions of just a 20th of a wavelength – that is about 20 nm for visible light, and much smaller than Abbe’s limit of about half a wavelength. But limitations then surfaced.
One of these is to do with the negative-index materials, which are typically thin slabs of metal such as silver. Metals absorb light, particularly the part that carries the higher-resolution information. Another limitation is that superlenses must be sandwiched flush between the object being imaged and the detector. Only at this close range, in the so-called near field, can a superlens transfer all the information about the object to the image. So while in principle a superlens can produce images with unprecedented resolution, in practice it has limited use: it must be placed awkwardly close to the object, and even then the images appear grainy.
While in principle a superlens can produce images with unprecedented resolution, in practice it has limited use
These problems have not totally spelt the end for superlenses. One promising variation is the hyperlens, developed independently in 2006 by theorists Alessandro Salandrino and Nader Engheta at the University of Pennsylvania in Philadelphia, US, and Evgenii Narimanov, then at Princeton University in the US, and colleagues. Based on alternating layers of positively and negatively refracting material, the hyperlens can collect sub-diffraction-limited information from an object, just like a superlens can. Unlike a superlens, however, the hyperlens transfers this information to an image away from the near field into the far field. This means the hyperlens should be able to be integrated with more conventional optics, making it more attractive for practical applications.
The downside of the hyperlens is that, like its progenitor, it absorbs light, so reducing fidelity. “Loss is indeed an issue for all metal-related lenses,” says Zhaowei Liu, a physicist at the University of California, San Diego, US, who studies superlenses and hyperlenses. “But if you care about resolution more than transmission, then [superlenses and hyperlenses] are still okay. If things are really small, you can still see them – you just need to use really strong laser light.”
Back in time
Unfortunately, in many lines of research – biological imaging, say – intense laser light may not be an option, particularly if you want to avoid damaging your sample. But Geoffroy Lerosey, Mathias Fink and others at ESPCI ParisTech in France have shown that there is a way to achieve sub-diffraction-limited images without the drawbacks of superlenses or hyperlenses: so-called time reversal. So far, the group has demonstrated time reversal only for microwaves, which have fairly long wavelengths and are easier to manipulate than visible light. Nonetheless, at a conference in Barcelona, Spain, last year the researchers revealed numerical simulations suggesting that visible-light time reversal could also be a possibility.
So why does reversing time help beat the diffraction limit? The answer lies in evanescent waves: constituents of a normal wave that contain all the sub-diffraction-limited information. Evanescent waves usually peter out within a couple of wavelengths’ distance from an object – this is where the near field ends and the far field begins – which is why conventional lenses cannot see past the diffraction limit. It was only by effectively amplifying evanescent waves, using negative refraction, that Pendry showed superlenses were not restricted in this way. But Lerosey, Fink and others took a new tack to capture these fickle undulations: fooling emitted light into thinking it is going backwards, towards the source.
To see how this works, consider a demonstration performed by the researchers in 2007. The experiment consists of a group of antennas, each separated by a 30th of a wavelength – far less than the diffraction limit. One antenna in the group emits a microwave signal, which travels across a chamber to a second group of antennas. Upon receiving the signal, this second group of antennas – each of which is separated by half a wavelength – replays it backwards, like running a tape in reverse. As this time-reversed signal propagates, it interferes with itself in such a way that it converges towards the antenna in the first group that originally emitted it, almost as though it were travelling back in time (see box “A new way of seeing things”).
A new way of seeing things
Time-reversal imaging
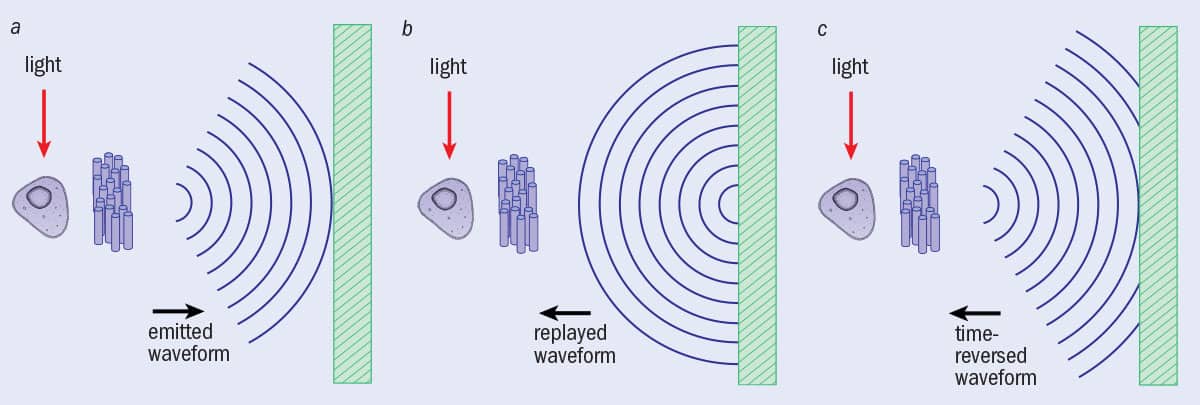 A biological cell is placed near to a resonant metalens, a random collection of tiny oscillators. (a) Upon illumination, a cell shines through the metalens, which converts the evanescent light waves into propagating waves. This waveform reaches a sensor array (right). (b) If the waveform were simply recorded and re-emitted, it would spread out. (c) However, if the waveform is time-reversed before being emitted again, the waveform interferes with itself in such a way that it perfectly converges back to the source. But this last step does not have to be done in practice: an algorithm can predict what would happen were the time-reversed waveform to be emitted, creating a computer-based image with details smaller than the diffraction limit.
A biological cell is placed near to a resonant metalens, a random collection of tiny oscillators. (a) Upon illumination, a cell shines through the metalens, which converts the evanescent light waves into propagating waves. This waveform reaches a sensor array (right). (b) If the waveform were simply recorded and re-emitted, it would spread out. (c) However, if the waveform is time-reversed before being emitted again, the waveform interferes with itself in such a way that it perfectly converges back to the source. But this last step does not have to be done in practice: an algorithm can predict what would happen were the time-reversed waveform to be emitted, creating a computer-based image with details smaller than the diffraction limit.
Maxwell’s fisheye
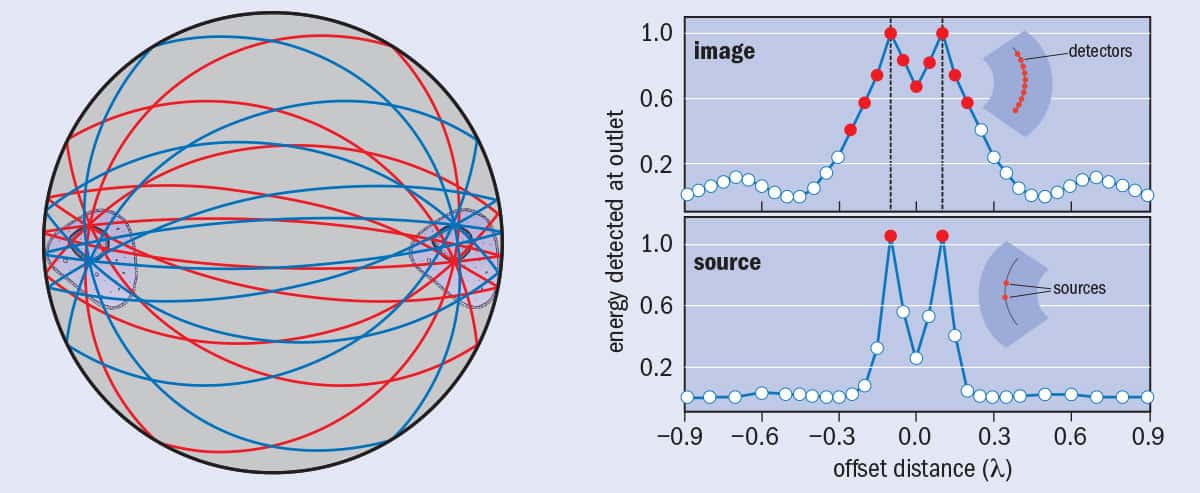 Maxwell’s fisheye is a flat lens with a spatially varying refractive index, which causes all light rays emitted from one point on the lens to meet at a point exactly opposite. In the design for a practical fisheye by Ulf Leonhardt and others (a), a mirror surrounds the lens, which enables an object to be placed not just on the surface of the lens but anywhere within it and still be imaged. In an experiment, Leonhardt’s group placed two microwave sources separated by a fifth of a wavelength on one side of the lens, and on the other side a bank of dissimilar microwave detectors separated by a 20th of a wavelength. (b) Only the detectors precisely opposite the two sources registered peak microwave signals. The researchers believe this is evidence that Maxwell’s fisheye can image beyond the diffraction limit.
Maxwell’s fisheye is a flat lens with a spatially varying refractive index, which causes all light rays emitted from one point on the lens to meet at a point exactly opposite. In the design for a practical fisheye by Ulf Leonhardt and others (a), a mirror surrounds the lens, which enables an object to be placed not just on the surface of the lens but anywhere within it and still be imaged. In an experiment, Leonhardt’s group placed two microwave sources separated by a fifth of a wavelength on one side of the lens, and on the other side a bank of dissimilar microwave detectors separated by a 20th of a wavelength. (b) Only the detectors precisely opposite the two sources registered peak microwave signals. The researchers believe this is evidence that Maxwell’s fisheye can image beyond the diffraction limit.
Scattering-lens technique
 The amount of light collected by a lens – defined by the lens’s numerical aperture – is key to imaging with higher resolution. According to Abbe’s formula, the greater the numerical aperture, the smaller the diffraction limit. (a) Even a large conventional lens struggles to collect much of the light emitted by an object – a lot passes by the sides. (b) A scattering layer placed before a lens captures light that would otherwise have been lost, thanks to the random path taken by light rays as they pass through the layer.
The amount of light collected by a lens – defined by the lens’s numerical aperture – is key to imaging with higher resolution. According to Abbe’s formula, the greater the numerical aperture, the smaller the diffraction limit. (a) Even a large conventional lens struggles to collect much of the light emitted by an object – a lot passes by the sides. (b) A scattering layer placed before a lens captures light that would otherwise have been lost, thanks to the random path taken by light rays as they pass through the layer.
On its own, this process does not precisely focus the signal onto the antenna that originally emitted it. That is because the crucial evanescent waves never reached the second group of antennas – they would have already decayed. But here Lerosey, Fink and colleagues have another trick: they surround each antenna in the first group with a random collection of thin copper wires – a “resonant metalens”, in their terms – like a tuft of hair. This time, as an antenna in the first group emits a signal, the evanescent waves resonate with the wires and convert into propagating waves, which are detectable by the second antenna group. Now, upon time reversal, the signal focuses precisely back onto the source antenna and none of its neighbours, despite their being only a 30th of a wavelength away (Science 315 1120). The fact that only the source antenna receives a signal shows that the imaging is truly sub-wavelength; if it were not, many neighbouring antennas – being closer to the source antenna than the diffraction limit – would also receive a signal.
Focusing a signal perfectly at its source would not be very useful for practical imaging – it only demonstrates that time reversal works. But in theory the focus point does not have to exist in the real world. To actually image something, you would only have to do a virtual time reversal – that is, record the incoming signal, calculate what the time-reversed waveform would look like, and then use software to predict the image that would have been produced. So unlike the image of a conventional lens, which is physically real, the time-reversed image would exist only in an algorithm’s output on a computer.
Let us say a biophysicist wanted to image a living cell. They would first place the cell within or near a resonant metalens and illuminate it with the necessary radiation – in this case, visible light. The signal from the cell, including the converted evanescent waves, would travel towards a bank of optical sensors, which would record it onto a computer. Then the computer would perform the time reversal and calculate the image that would be produced if the time-reversed signal were to propagate in real space.
Old idea
It is not yet clear whether the ESPCI researchers’ method will work in practice with visible light, for which record–playback time reversal will be much trickier. However, perhaps a simpler way to perform time reversal was dreamed up one morning in the early 1850s when James Clerk Maxwell, then a student at Cambridge University, was poking at his breakfast. According to legend, Maxwell was examining the kipper before him when he came up with the idea for a fisheye lens – a flat lens with a varying refractive-index profile that would cause light rays to travel in arcs, perfectly transferring all light rays emanating from one side to a point opposite.
Physicists had assumed Maxwell’s fisheye would not produce perfect images in practice, but in 2009 Ulf Leonhardt, a physicist at the University of St Andrews in the UK, predicted otherwise. Using Einstein’s equations of general relativity, Leonhardt showed that light rays emitted by an object on the surface of the fisheye would, in optical space, hug the surface of a sphere, travelling in great semi-circles that always meet at a point precisely opposite the starting point. This unique symmetry would mean that, on approaching the image point, the light rays would be acting as though they were travelling backwards in time towards the source. And this, said Leonhardt, meant perfect images.

It was a controversial prediction, not least because it meant perfect imaging could be possible without negative refraction and, therefore, without loss – one of the main pitfalls of the superlens. But within two years Leonhardt – working with his student Yun Gui Ma, then at the National University of Singapore, and others – had experimental evidence that he was right. Their device used concentric rings of copper to achieve Maxwell’s refractive-index profile and, like the ESPCI researchers’ device, worked only for microwaves. Signals entered the fisheye via two sources a fifth of a wavelength apart and travelled across the device, into the far field, to a bank of 10 outlets a 20th of a wavelength apart.
If the fisheye did not exhibit perfect imaging, you would expect the output signal to be smoothed out over the outlets, because all 10 would span the diffraction limit of half a wavelength. Instead, the group found strong peaks at the two outlets that were precisely opposite the sources, separated by just a fifth of a wavelength (see box “A new way of seeing things”). For Leonhardt, this was sure evidence of imaging beyond the diffraction limit (New J. Phys. 13 033016).
He has had to fight to convince others, however. One critic is Pendry, who believes the outlets record sub-wavelength features only because the outlets are “clones” of the source. Other sceptics go a step further and say that the signal peaks arise because of well-known field localization at the outlets, just as a lightning rod focuses electric fields around its tip. In December 2011 Richard Blaikie, then at the University of Canterbury in Christchurch, New Zealand, published results of a simulation in which a microwave source is contained within an empty mirrored cavity – that is, where there is no lens or refraction at all. He found that sub-wavelength focusing appeared when he added an outlet, or “drain” (New J. Phys. 13 125006).
“The sub-wavelength field enhancement at or around the image point only occurs when the drain is present,” Blaikie writes. “The nature of the perfect imaging that has been the [cause] of much recent excitement is solely due to drain-induced effects.”
Leonhardt thinks his critics are missing the point. In his fisheye experiment there was not just one drain but 10. If Blaikie and others were right – that the perfect imaging is an artefact of the drains – then the field should have localized over each of them, since they were all spaced within the diffraction limit. Instead, the field localized only over the two drains precisely opposite the sources. Leonhardt believes the only way he will convince his sceptics will be to repeat the experiment in optics, a much more fiddly regime.
Beyond the limit
There are several other methods that have been shown to beat the diffraction limit. One of these, proposed in 2006 by Michael Berry and Sandu Popescu of the University of Bristol in the UK, involves so-called superoscillations. These are special types of wave, created in a hot-spot of many laser beams interfering with one another, that persist long enough for sub-wavelength information to transfer to the far field. In 2009 Fu Min Huang and Nikolay Zheludev of the University of Southampton in the UK showed experimentally that superoscillations could be used to focus light to a point as small as a fifth of a wavelength across. Unfortunately, the focus spot comes at a cost: an accompanying bright, unfocused halo of light, which might make imaging difficult in practice.
Another option was demonstrated last year by Zengbo Wang of the University of Manchester (now of Bangor University) in the UK and colleagues. Known as virtual imaging, it involves placing transparent spheres, each less than 9 µm across, onto an object, before shining white light up from beneath. The spheres essentially magnify the near-field light coming from the object to a size detectable by a camera above, offering a resolution of about 50 nm – about a quarter of the typical diffraction limit.
Finally, there is a way to see sub-wavelength details in the far field without using any special apparatus at all – just computer software. Developed by Mordechai Segev and colleagues at the Technion Israel Institute of Technology, it involves examining an image’s Fourier transform, which depicts wave components. For a diffraction-limited image, the Fourier transform would be incomplete. Segev and colleagues’ software therefore calculates the simplest wave components that would complete the Fourier transform and then adds them, essentially filling in the gaps by guessing what it expects to be there. The good news is unlimited resolution; the bad news is that – even in principle – it works only for sparse, technical images in which most pixels are blank. So if you were thinking of touching up your holiday snaps, think again.
Doing the opposite
Perhaps Leonhardt’s problem is that he is almost speaking a new language in optics. For example, he thinks the traditional distinction between the near field and the far field is a myth, particularly the notion that certain information is always lost in the far field. Yet among many sceptics, a few physicists think he might be onto something. “Leonhardt [is] one of the smartest people I ever met,” says Jacopo Bertolotti of the University of Twente in the Netherlands. “If he says Maxwell’s fisheye should work, he is saying it with many good reasons.”
In the meantime, Bertolotti, together with Allard Mosk and others at Twente, already has what may be the most impressive results yet for high-resolution imaging. Amazingly, though, the technique does not involve transferring light cleanly from source to image, but rather the opposite: scattering light in all directions (see box “A new way of seeing things”).
The reason for this counterintuitive approach is that Abbe’s diffraction limit depends not just on the wavelength of light being used, λ, but also on another property of the lens: the numerical aperture, nsinα, where n is the refractive index and α is the half-angle of the maximum cone of light that can enter the lens. In fact, the diffraction limit – the best resolution possible and the formula on Abbe’s memorial – is defined as λ/2nsinα. Similar to the aperture of a camera lens, the numerical aperture is a parameter that defines the range of angles over which a lens can collect light from an object. The greater the numerical aperture, the more light is collected – and the smaller the diffraction limit.

Unfortunately, a big numerical aperture needs a big lens to collect lots of light. This is difficult for conventional lenses, which need a very high, well-tailored refractive index to bend light coming from the edges of an object back towards an image point. For these conventional lenses the biggest numerical aperture possible has a value of about 1, which is why the diffraction limit is usually about half a wavelength. A scattering lens offers a cheaper, easier way to achieve greater bending: light leaving the lens is sent randomly in almost all directions, which is good as it means some of it is bent through very large angles indeed. But the trouble is that the resultant image is a fuzzy, out-of-phase mess.
To avoid this problem, Bertolotti, Mosk and colleagues use a clever feedback mechanism that pre-adjusts the phase of the light reaching the scattering lens so that, once it passes through, it is in-phase again and not fuzzy. The light is pre-adjusted using a device known as a spatial light modulator, which is placed before the lens. To calibrate the modulator so that it changes the light’s phase by the right amount, a detector placed after the lens sends a test image to a computer, where it is analysed using an algorithm. The algorithm looks at the phase of the different parts of the test image and calculates how the spatial light modulator should compensate for the scattering by adjusting the phase of light going into the lens. Once the adjustment required is known, the modulator adjusts incoming light accordingly and any subsequent images taken using the scattering lens are in-phase and clear.
Last year, the Twente researchers tested their concept with a lens made from gallium phosphide, which they roughened on one side to scatter incoming light. They found that it could image, at a visible wavelength of 560 nm, gold nanoparticles with a resolution of just 97 nm (Phys. Rev. Lett. 106 193905).
Praise for the Twente researchers’ work is high. “This is wonderful stuff,” says Leonhardt. “It is so non-intuitive. You make things worse to make things better.” Lerosey at ESPCI Paris Tech is also impressed, saying “It’s a good idea, it’s a nice group of concepts.” He adds that the field of view – the amount seeable by the lens – is not great, but then that is a practical hurdle that all these new techniques will have to overcome.
Of course, the catch with the scattering lens is that it does not actually beat the diffraction limit. The resolution may be nearly a sixth of the light’s wavelength, but it is within the confines of Abbe’s formula, which allows greater resolution so long as the numerical aperture increases – and in this case it is about 3. Conventional lenses cannot achieve sufficient apertures to resolve details finer than half a wavelength, but the scattering lens can – not with better quality optics, but with a neat use of computing technology.
So maybe there is a lesson to be learned. While there are now several promising approaches in addition to superlenses to smash Abbe’s diffraction limit, the best option for achieving sub-wavelength imaging in practice might well be to leave it intact. Setting the equation in stone was perhaps not such a bad idea, after all.
- This article first appeared in the May 2012 issue of Physics World.