Thomas Young’s double-slit experiment is famous for demonstrating the principle of interference. Andrew Murray explains why it’s now possible to carry out an equivalent experiment using lasers that have excited individual rubidium atoms
Over the last 20 years I must have spoken to more than 400 school pupils who want to study physics here at the University of Manchester. One subject that regularly comes up at interview is Young’s double-slit experiments, which clearly interest my prospective students. But when I ask them what the experiments are all about, I’m invariably told they involve using electrons to demonstrate wave–particle duality – one of the cornerstones of quantum physics. That’s curious because Thomas Young performed his experiments in 1804 – long before we knew anything about electrons or the subatomic world.
Young’s original double-slit experiments were in fact the first to demonstrate the phenomenon of interference. When he shone light through two narrow slits and observed the pattern created on a distant screen, Young didn’t find two bright regions corresponding to the slits, but instead saw bright and dark fringes. He explained this unexpected observation by proposing that light is a wave, in opposition to Newton’s idea that light is made of particles. These experiments, and their subsequent explanation, culminated in the classical laws of radiation enveloped by James Clerk Maxwell’s famous equations.
From Young’s double slits to wave–particle duality

The remarkable success of the wave theory of light, inspired by Thomas Young’s original double-slit experiments of 1804, was marred by two later observations that did not fit the theory. One was the measurement of the radiation density emitted by a blackbody, which could not be explained using the accepted laws of radiation formulated by Lord Rayleigh and James Jeans – the so-called “ultraviolet catastrophe”. This problem led Max Planck in 1900 to develop an alternative theory, which assumed blackbody radiators have discrete (quantized) energies, from which he successfully predicted the experimental data.
The second problem was the photoelectric effect – that light can kick out electrons from a material but only if it’s above a certain frequency. Extending Planck’s ideas, Albert Einstein was able to explain this phenomenon by predicting that the radiation is quantized. This insight also let him predict that the intensity of light depends on the rate at which these particles of fixed energy (later called photons) are detected. Wave theory, in contrast, stated that the intensity should be proportional to the square of the amplitude of the wave. Further work by Ernest Rutherford and Niels Bohr in Manchester led to the development of the “old” quantum theory, which explained the structure of atoms and why their spectra were discrete.
Several years later, Louis de Broglie suggested that if light can be considered as having both wave- and particle-like properties, then perhaps matter also has a dual nature. Experimental evidence supporting this soon followed, from which Erwin Schrödinger, Werner Heisenberg and Paul Dirac developed the modern form of quantum mechanics we use today. Only in the 1960s did the link between Young’s double-slit experiment and wave–particle duality become clear when it was carried out for the first time with an electron beam.
The link between Young’s experiments and wave–particle duality only became obvious last century once the basics of quantum mechanics had been firmly established (see box above). The story began in 1961 – more than 130 years after Young’s death – when Claus Jönsson from the University of Tübingen in Germany machined a set of slits 300 nm wide into copper and then irradiated them with a 40 keV beam of electrons from an electron microscope (Z. für Physik 161 454). The resulting images showed an interference pattern, just as Young had first seen with light 160 years earlier. This first double-slit experiment with electrons indicated that an electron beam behaves as a wave. But since Jönsson couldn’t create or measure individual electrons, he couldn’t prove that each electron itself has a wave-like character.
In 1965 Richard Feynman then gave a now-famous series of lectures at the California Institute of Technology, in which he discussed how single electrons fired at a double slit would, in principle, produce an interference pattern – thereby demonstrating the dual wave–particle nature of matter. Feynman did not think his thought experiments would ever be possible, but over the next few decades, advances in manufacturing techniques gradually brought this prospect closer. Eventually, in the mid-2000s Stefano Frabboni and co-workers in Italy demonstrated interference with electrons passing through slits just 83 nm wide (2007 Am. J. Phys. 75 1053 and 2008 Appl. Phys. Lett. 93 073108).
Using an electron microscope operating at 200 keV, Frabboni and his team were able to reduce the beam current to such low levels that they could predict with a very high probability that no more than one electron was between the source and detector at any given time. But because their detector had various limitations, they couldn’t directly measure interference from single electrons. It was not until 2013 that the first experiments to convincingly demonstrate double-slit interference using single electrons were finally carried out (figure 1).
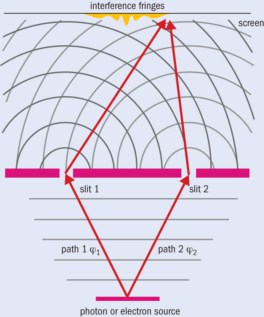
1 Young’s double-slit experiment with single electrons
If you fire single particles, such as photons or electrons, through two slits labelled 1 and 2, the wavefunctions ϕ1 and ϕ2 along each path describe the probability that they will pass through the slits, with the total wavefunction at the detector being ϕdet = ϕ1 + ϕ2. The probability of detecting a particle is then ϕdet2 = ϕ12 + ϕ22 + 2|ϕ1||ϕ2| cos Δξ, where |ϕ1| and |ϕ2| are the amplitudes of the waves and Δξ is their phase difference at the detector. The result is a series of bright and dark bands depending on whether the two wave fronts are in phase (cos Δξ = 1) or out of phase (cos Δξ = –1), meaning either a high or low chance of detecting a particle. But if you close, say, slit 2, then ϕ2 = 0 and you see a distribution of particles due solely to slit 1 (ϕdet2 = ϕ12). If you close slit 1, then ϕ1 = 0 and the distribution is given by (ϕdet2 = ϕ22). You can work out the interference term by measuring the signals from both slits individually, and by then measuring the yield with both slits open.
Working at the University of Nebraska-Lincoln in the US, Roger Bach and co-workers used 62 nm wide slits, through which they fired electrons with a beam energy of just 0.6 keV. This much lower energy, which increased the de Broglie wavelength of the electrons compared with previous experiments, not only produced a wider separation of the interference pattern, but also allowed them to use a channel plate detector that could count single electrons. The experiment also let Bach’s team physically move a mask across the slits so that each could be individually closed, or both could be open.
In these experiments, Bach’s team reduced the intensity of the incident beam so that only one electron was detected each second, thereby guaranteeing (to greater than 99.9999% probability) that only a single electron was present between the source and the detector at any time. The experiment ran continuously for two hours and, initially, the individual electrons appeared to arrive at random points on the screen. But as more and more electrons were detected, an interference pattern with bright and dark regions gradually emerged (2013 New J. Phys. 15 033018).
Since each electron was detected before the next was emitted, it clearly could not have influenced future electrons that then passed through the slits. As elegantly stated by Feynman, we therefore have to accept that each electron (and indeed all matter) has both a wave-like nature (to create the interference pattern) and must also be considered as an individual particle (since this is what was detected). It is therefore this double-slit experiment, not Young’s from 1804, that future students at Manchester should be citing when they talk about wave–particle duality.
The new experiments in a single atom
Now if you think that’s about as far as a Young’s double-slit experiment can go, you’d be wrong. In one of those rewarding occasions in science when new discoveries and ideas evolve from seemingly unrelated work, our research group in Manchester recently found an entirely new way to carry out the experiment. The discovery emerged from our studies of the “shape” that atoms adopt when we excite them with laser light and then fire electrons at them. The electrons gain energy as the atoms are de-excited and we catch these scattered electrons at different angles.
We’d known a lot about this “super-elastic” collision process – in fact, we’d studied it for years. But when we used 420.30 nm blue light to excite a particular state in rubidium atoms, known as the 6P state, we were in for a surprise (2019 Phys. Rev. Lett. 122 053204). This time we couldn’t find any electrons from the super-elastic collision process. So why, we wondered, was there no signal?
It turns out that the experiment was producing lots of photoelectrons from the laser beam (we could see these even with the incident electron beam off), but they were all at low energies. In fact, these photoelectrons emerged with four different energies in such large quantities that they drowned out the super-elastic signal we were expecting. The photoelectrons came not only from the 6P state, but also from lower states that the atoms could relax back to, including 0.36 eV electrons kicked out of the 5P state (figure 2a).
But what’s this got to do with the double-slit experiment? Well, this is where our new idea came in. We realized that if we fired a second, infrared laser beam with a wavelength of 780.24 nm at the atoms, this light could not only excite the atom to the 5P state, but also ionize the 6P state, producing photoelectrons with an energy of 0.36 eV. This is exactly the same energy as the photoelectrons created when blue light ionizes rubidium atoms in the 5P state.
There are, in other words, two possible paths that produce photoelectrons at this energy (figure 2b). The laser beams effectively “guide” the photoionization process so it goes either through the 5P state with a wavefunction Ψ1 (equivalent to slit 1 in a conventional Young’s double-slit experiment), or through the 6P state with a wavefunction Ψ2 (equivalent to slit 2), or simultaneously via both states. Rather than measuring the intensity of photons or electrons on a screen, we instead count the number of photoelectrons at different angles, θ, relative to the polarization of the laser beams – what’s known as the differential cross-section, DCS(θ).
2 Young’s double-slits with a single atom
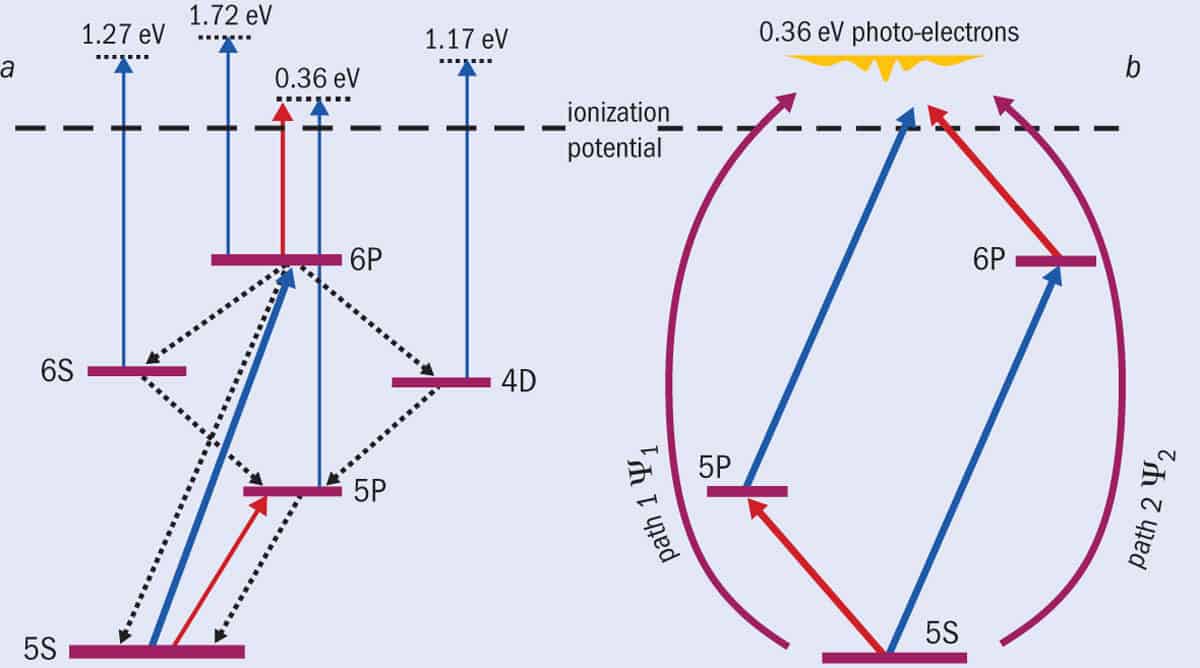 (a) Our new version of Young’s double-slit experiment doesn’t involve firing particles through slits but uses lasers to excite rubidium atoms in different ways. Shining blue 420.30 nm laser light excites the atom from the 5S to the 6P state (transition indicated by thick blue arrow). The 6P state then relaxes to two other states (4D and 6S) that in turn relax back to a fourth state (5P) – the relaxations shown by dotted arrows. Additional blue photons (also 420.30 nm wavelength) can then ionize these states, releasing photoelectrons at four different energies (represented by narrow blue arrows), including at 0.36 eV. By using a second, infrared laser at 780.24 nm, we can either excite the rubidium atom to the 5P state or produce a photoelectron from the 6P state (red arrows), also at 0.36 eV. (b) If we set our detector to measure only the 0.36 eV electrons, they come from two possible paths – either via the 6P state ionized by the infrared laser, or via the 5P state ionized by the blue laser. The two paths can be turned on or off, just as we can open or close the slits in a conventional double-slit experiment.
(a) Our new version of Young’s double-slit experiment doesn’t involve firing particles through slits but uses lasers to excite rubidium atoms in different ways. Shining blue 420.30 nm laser light excites the atom from the 5S to the 6P state (transition indicated by thick blue arrow). The 6P state then relaxes to two other states (4D and 6S) that in turn relax back to a fourth state (5P) – the relaxations shown by dotted arrows. Additional blue photons (also 420.30 nm wavelength) can then ionize these states, releasing photoelectrons at four different energies (represented by narrow blue arrows), including at 0.36 eV. By using a second, infrared laser at 780.24 nm, we can either excite the rubidium atom to the 5P state or produce a photoelectron from the 6P state (red arrows), also at 0.36 eV. (b) If we set our detector to measure only the 0.36 eV electrons, they come from two possible paths – either via the 6P state ionized by the infrared laser, or via the 5P state ionized by the blue laser. The two paths can be turned on or off, just as we can open or close the slits in a conventional double-slit experiment.
By slightly detuning the frequency of one or other of the lasers, we can turn the pathways on or off, just as we can physically open or close the slits in a conventional Young’s double-slit experiment. Detune the blue laser and you excite only the 5P state, which closes path 2 and gives a photoelectron yield of DCS1(θ) ∝ Ψ12, where θ is the scattering angle. Detune the infrared laser, and you only excite the 6P state, closing path 1 and giving DCS2(θ) ∝ Ψ22. When both lasers are on resonance, both states are excited, and we have to add the wavefunctions to give DCS1+2(θ) ∝ (Ψ1 + Ψ2)2 .
In the same way as for Young’s experiments, we end up with an interference pattern. The interference term DCSinterf(θ) is, in fact, proportional to 2|Ψ1||Ψ2| cos Δχ, where |Ψ1| and |Ψ2| are the amplitudes along each pathway and Δχ is the relative phase shift between the waves at the detector. We can determine DCSinterf(θ) by taking three sets of measurements: one with both lasers on resonance yielding DCS1+2(θ), another with the blue laser off-resonance producing DCS1(θ), and a third with the infrared laser off resonance producing DCS2(θ).
Theory versus experiment
One practical challenge with our new double-slit experiments was finding a way to detect photoelectrons having just 0.36 eV of energy, which is 600,000 times lower than used in the earlier electron-microscope studies. We solved this be carefully eliminating magnetic and electric fields in the experiment that would otherwise have influenced the electrons as they emerged from the atoms, and by building detectors that could select and count single electrons at this energy.
So what did our experiments reveal?
3 From idea to experiment
 In our equivalent of Young’s double-slit experiment, we use a beam of rubidium atoms emitted from an oven inside a vacuum chamber. We then fire blue and infrared lasers at the rubidium, feeding the beams vertically into the chamber and rotating their polarization through 360° to determine the number of photoelectrons at different angles. This plot shows the measured “differential cross-section”, DCSinterf(θ), and the “relative phase shift”, Δχ = χ1 (θ) – χ2 (θ) between the two possible ionization pathways that lead to 0.36 eV photoelectrons. If no interference occurred between the pathways, DCSinterf(θ) would be zero, and Δχ would also be 0. The fact that the values are clearly not 0 – and agree with theoretical calculations – shows that the photoelectrons have both wave-like and particle-like properties, thereby confirming wave–particle duality.
In our equivalent of Young’s double-slit experiment, we use a beam of rubidium atoms emitted from an oven inside a vacuum chamber. We then fire blue and infrared lasers at the rubidium, feeding the beams vertically into the chamber and rotating their polarization through 360° to determine the number of photoelectrons at different angles. This plot shows the measured “differential cross-section”, DCSinterf(θ), and the “relative phase shift”, Δχ = χ1 (θ) – χ2 (θ) between the two possible ionization pathways that lead to 0.36 eV photoelectrons. If no interference occurred between the pathways, DCSinterf(θ) would be zero, and Δχ would also be 0. The fact that the values are clearly not 0 – and agree with theoretical calculations – shows that the photoelectrons have both wave-like and particle-like properties, thereby confirming wave–particle duality.
If there was no interference between the two ionization pathways – as we’d expect from a classical interpretation of the ionization process – then both the interference term and the relative phase shift should be zero at all angles. But the values were not zero (figure 3). The interference term, for example, varied from –0.14 to –0.56, proving that there was significant interference between the two pathways. The average phase shift, meanwhile, was Δχ = 115°, which is also far from 0. This clearly demonstrated that the individual electrons emerging from each atom must therefore have a wave-like nature, until they are detected as real particles by the detector. In fact, our results were in excellent agreement with calculations carried out by Jonas Wätzel and Jamal Berakdar – two experts in quantum calculations of photo-ionization processes at the Martin-Luther University in Halle, Germany.
Looking to the future, we are now extending and refining our models to study interference in other atoms, for other states and under different regimes. Recently, for example, they’ve been applied to excitation using femtosecond lasers (2019 Phys. Rev. A 100 013407). Further theoretical studies show that the interference terms can be dramatically enhanced by choosing atomic states that are close in energy, and indeed there is no reason why the initial state needs to be the ground state – we can equally explore what happens when the process starts with an excited atom. This could help us understand the atmospheres of stars, where the constituent atoms are often in excited states. Further possibilities lie in two-path excitation to highly excited Rydberg atoms, in which the electrons are so far from the nucleus that the atoms are as big as a living cell – and could therefore be used in quantum computers.
The possibilities are limited only by our imagination, which is what makes physics such an exciting and rewarding endeavour.