Recent experiments in fluid mechanics are shedding light on the intricate motion displayed by non-spherical objects as they fall, a problem that has puzzled physicists for centuries and still defies a full theoretical explanation.

In the mid-17th century Galileo Galilei dropped two metal balls from the Leaning Tower of Pisa and showed that they fall at the same rate despite their different masses. In a later version of the experiment, astronaut David Scott dropped a hammer and a feather on the Moon and saw that they hit the surface at the same time. Why did Galileo not choose this more dramatic combination of objects to drop from the Leaning Tower?
While air resistance leads to shape-dependent drag, dropping a feather would have been a particularly poor choice for another, more interesting reason. Most of us know from experience that feathers “flutter” from side to side as they drift slowly towards the ground. They certainly do not fall in a straight line. What special property do feathers possess – in common with sheets of paper, playing cards, autumn leaves and coins flipped into a wishing well – that allows them to partially ignore the downward pull of gravity? The graceful and intricate motion displayed by these objects is due to the fluid around them, which couples the downward motion to lateral or sideways excursions. In contrast, on the Moon a feather drops like a stone because there is no atmosphere.
Although James Clerk Maxwell first considered the motion of an object falling freely though air over 150 years ago, the equations remain unsolved today for the most general case. Nonetheless, fascinating and sometimes orderly effects present themselves and beg to be understood. Ultimately, they are related to one of the last puzzles of classical physics: fluid dynamic instability. This challenging problem spans the scale from micro-organisms swimming through fluids to atmospheric turbulence.
Simplifying the motion
The effect of the surrounding fluid on a falling object’s motion has far-reaching consequences in everyday applications, both man-made and natural. Flying and swimming are practised under the influence of the same forces that cause a feather to flutter from side to side. Every non-spherical object moving with a high enough velocity encounters forces that can cause it to tumble or flutter.
Maxwell noted that the forces exerted by gravity and the fluid do not necessarily act at the same point, and thus can create a torque. The details of the fluid forces depend not only on the shape of the moving body but also on the presence and location of swirls of fluid motion called “vortices”. These differ from case to case, creating a rich variety of applications in engineering and nature. As is often the case in complicated, highly nonlinear systems, the equations that describe the problem in three dimensions are difficult to solve. The system therefore needs to be simplified before any progress can be made. The first step taken by theorists has been to constrain the motion to two dimensions. The problem is further simplified by ignoring vortices and by assuming that the fluid has zero viscosity. In the 1870s Gustav Kirchhoff showed that the problem could be further simplified to a set of equations that could be solved for simple shapes, even though his new equations contained over 20 new “added mass” terms. The same method appears in Horace Lamb’s classic treatise on hydrodynamics, and was most recently applied explicitly to the motion of falling paper by Lakshminarayanan Mahadevan at the Massachusetts Institute of Technology in the US. Is there anything more to be done on this subject?
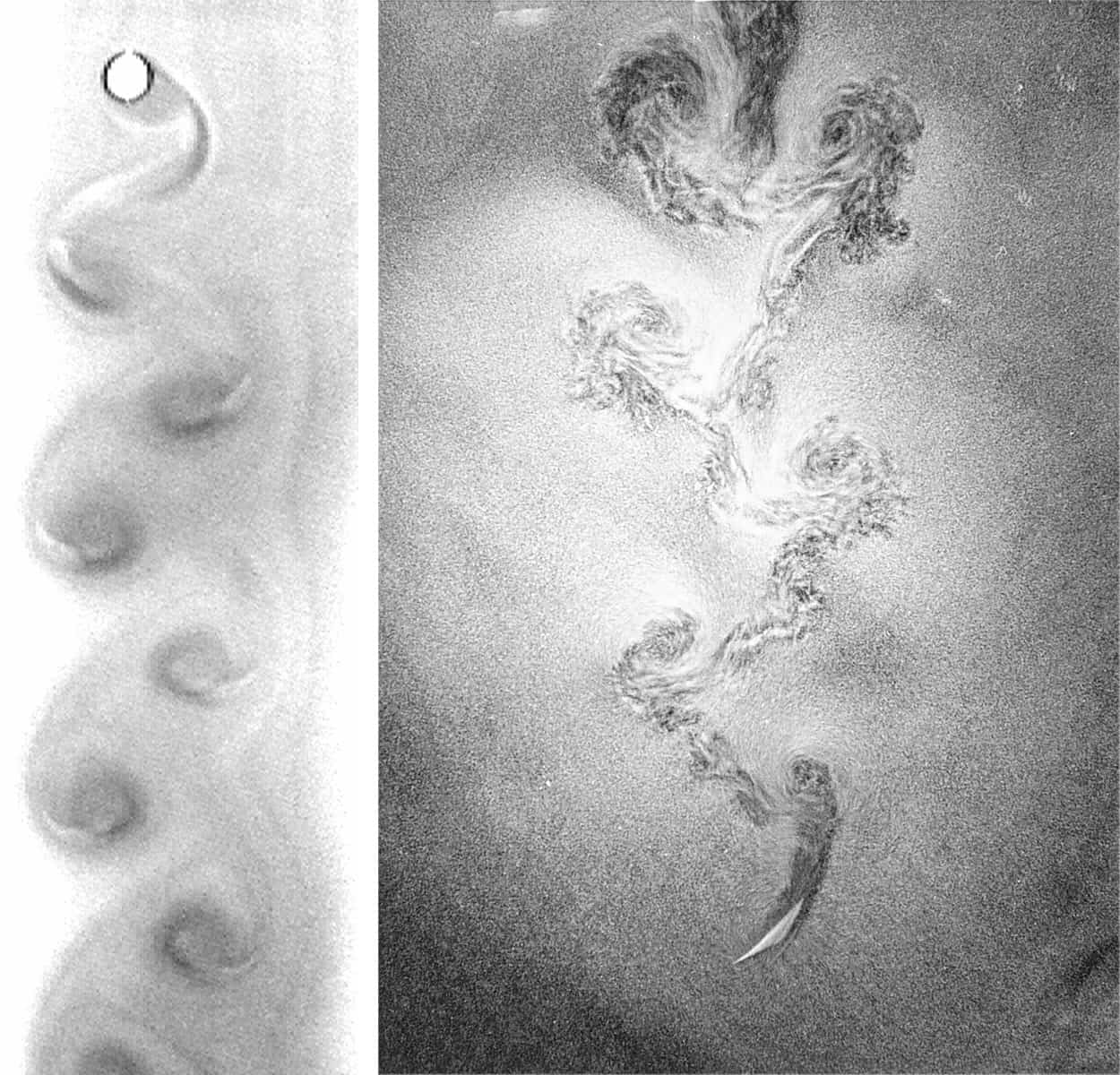
Although there are surprisingly few laboratory experiments devoted to the problem, the results show beyond doubt that there is a fundamental difficulty with the simplified theoretical approach. In the pioneering experimental work of William Willmarth at the University of Michigan in the 1960s, dye-laden discs were dropped into water and vortices were clearly seen in their wake. Recent experiments have confirmed that metal strips and air bubbles produce vortices as they fall or rise in a fluid (figure 1). Vortex production is such an important part of fluid dynamics that a complete theory must take it into account. Yet Willmarth’s experiment with Norman Hawk and Robert Harvey was the main study on the motion of falling objects before the recent flurry of activity in the 1990s.
There have also been a large number of laboratory studies of “autorotating” objects in wind or water tunnels. The efforts were mainly driven by practical considerations, such as the dynamics of aircraft after they stall, meteorological questions related to the formation of hailstones and the industrial problems of sedimentation.
All of the previous experiments on falling objects have been in three dimensions. Although fluttering, gyrating and tumbling behaviour have all been observed, very few quantitative details of the dynamics were given. The recent experiments in which we have been involved bring a new twist to the problem of falling through fluids. Our experiment is restricted to a two-dimensional system, which simplifies the situation considerably. More importantly, it eliminates a variety of modes of motion that tend to destabilize the falling object’s trajectory in 3-D, making it unpredictable and uncontrolled. It also means that a detailed comparison with the classic theoretical studies can be made. Our experimental effort began when Hagai Eisenberg, then a Masters student at the Weizmann Institute, walked into the laboratory and dropped a piece of paper. “This is what I want to study, ” he said pointing to the paper as it fluttered to the ground. By coincidence, Kunihiko Kaneko of Tokyo University had published an elegant and conceptually simple model of falling paper a few months earlier, using simulations of 2-D flow to identify chaotic regimes of motion. Kaneko and Yoshihiro Tanabe broke with tradition and allowed the circulation of the fluid to vary in their model. Although Tanabe and Kaneko did not explicitly consider the presence of vortices, this is a commonly made assumption in models of animal flight where vortices are known to play a role.
Moths, balls and aeroplane wings
For many moving objects, the surrounding fluid (air or water, for example) can exert a sideways force that is more subtle than the drag force. Any baseball pitcher or aeroplane pilot can confirm that the relative motion between an object and the fluid can produce lift. The forces that can make a spinning ball swerve or produce lift in an aeroplane are produced by a common cause: a net circulation of the fluid around the object (see, for example, ” The physics of football” Physics World June 1998).

This flow can be separated into translating and circulating components (figure 2). In the case of a baseball or a football, the reason for this circulation is clear: the fluid in contact with the ball rotates with it. The force perpendicular to the flow is directly proportional to the rotation rate, and can be explained in terms of Bernoulli’s law, which relates flow rate and pressure. The fluid moves faster on one side of the object than the other, and the resulting pressure difference exerts a force that can lift the ball or cause it to swerve. Although an aeroplane wing or aerofoil does not rotate, its shape or angle of inclination in the flow produces the same effect on the fluid. In this case the fluid circulation around the wing is not known. However, it can be determined by the Kutta-Zhukovski theorem, which states that the circulating component around the aerofoil is matched so that the flow field continues smoothly past the back edge of the wing. In steady-state situations, such as an aeroplane cruising at constant speed and altitude, the Kutta-Zhukovski theorem has been shown to be correct. But what about unsteady situations where the wings move vertically or flap?
The fluttering fall of paper and the way in which vortices are created have many similarities with the fluid dynamics associated with a bird flapping its wings. No insect, bird or mammal flies in the way a plane does, with rigid, outstretched wings (not to mention the high ground speed needed to take off). Moreover, the hydrodynamics of flapping pose certain conceptual difficulties for the explanation of lift, since the circulation around the wing is always changing. Charles Ellington at Cambridge University in the UK recently built a “mechanical moth” to study the way that momentarily stable vortices are created by the flapping wings and cause the moth to lift. Studying the way vortices are created by the fluttering motion of paper may lead to a better understanding of the physics of flight. Recent simulations by Jane Wang and Steve Childress at the Courant Institute in New York may also lead to new insights. To describe the motion of an object as it falls through a fluid with changing velocity, Tanabe and Kaneko assumed that the steady-state conditions could be applied at each instant. This involved using the Kutta-Zhukovski theorem to specify the lift produced by the fluid in the model of falling paper. We designed and constructed a quasi 2-D laboratory experiment that was accurate enough to check this model using real objects. By dropping thin flat strips of plastic, aluminium or steel in different fluids between two closely spaced glass plates, we observed two fundamental motions: side-to-side oscillations (flutter) and end-over-end rotation (tumble). Our experiment showed that the swinging motion of the falling strips was strikingly regular and was accompanied by a spectacular fluid flow. We found that the fluttering dynamics of the strips and the transition from fluttering to tumbling motion could be described by a single dimensionless parameter that was related to the shape of the strips.
Pushing fluids around
The two sources of drag for an object moving though a fluid are the viscosity of the fluid and its inertia. The viscous drag force comes from the “stickiness” of the fluid: the velocity of the fluid must match the velocity of the object at its surface, so the effects of the drag force are felt in the fluid as well. The viscous drag depends linearly on the relative velocity of the fluid to the object. The second source of drag, sometimes referred to as the “form drag” or “inertial drag”, depends on the density of the fluid rather than its viscosity. This force varies according to the square of the relative velocity of the fluid and the object.
Our falling strips have quite high Reynolds numbers (defined as the ratio of inertial force to the viscous force), of the order of 1000 to 10 000, which means that the inertial drag is more important than the viscous drag. This in turn means that the strips lose energy by transferring it to the fluid, leading to the creation of large flow structures. It also ties in with another observation, that vortices created by the falling object are intimately linked to its dynamics, being produced at every “zig” and “zag” of the fluttering object, or at every 180° turn in the tumbling regime (figure 3).
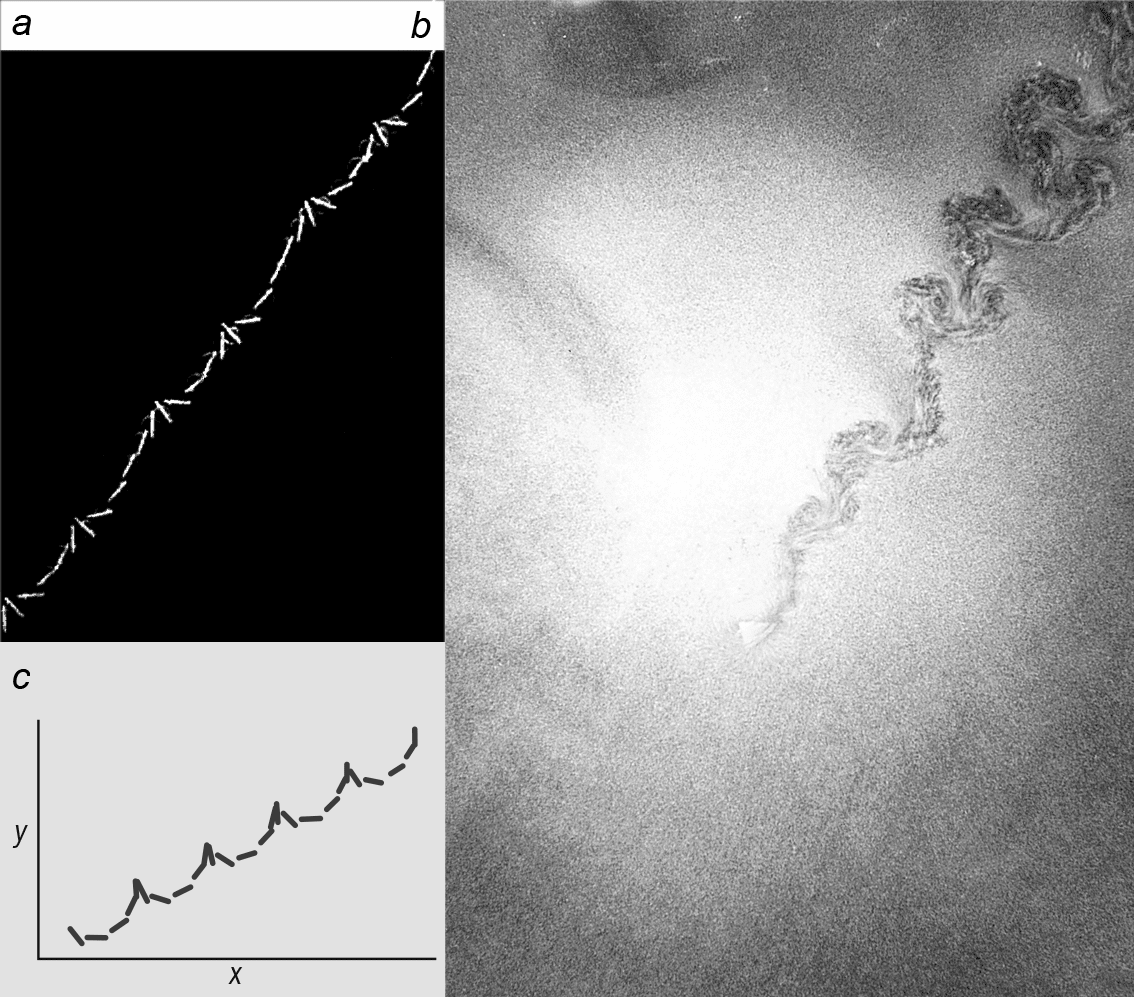
We also found that the mechanism determining whether the strips would tumble or flutter could be related to intrinsic properties of the strip itself. The transition from flutter to tumble is given precisely by a dimensionless quantity called the Froude number. For a falling object the Froude number measures the ratio between the typical timescales of falling and of swinging. (This number was originally introduced by William Froude in the 1870s to compare the performance of ships; it is the ratio of the ship’s speed to the speed of surface waves, which are the main source of drag.) For a falling object, the rotary motion – either the fluttering or tumbling – as vortices are shed is the main source of drag.
The strip also stores energy in a similar way to a pendulum. The Froude number thus characterizes the dissipative role of oscillations. Interestingly, it is also used to compare the way that animals, ranging from the rat to the rhinoceros, walk and run. In his monumental work on the physics of biological shapes, On Growth and Form, D’Arcy Wentworth Thompson discusses the “pendulum model” of walking, which accounts for the exchange between gravitational potential energy and swinging kinetic energy during a stride. Energy is expended when the foot makes contact with the ground and reverses the direction of its swing. This is analogous to the creation of a vortex by the strip. Moreover, recent studies of the transition from walking to running in bipeds, or to a brisk trot in quadrupeds, occur at a critical Froude number of 0.8; the transition from a trot to a gallop in quadrupeds then occurs at around a Froude number of 3.
The swinging motion of fluttering strips and walking legs are both limited by a common transition mechanism, which is essentially the “overturning point” of a simple pendulum. When driven hard enough, both legs and falling strips reach this pendulum limit and make a transition to the next, more complicated, mode of motion. For the fluttering strip, once it is given enough angular momentum, it flips over and executes a full rotation: in other words it tumbles. In the case of legs the transition is of course more complicated, but the end result is, if you want to go faster, you need to run. The transition of a pendulum driven to its overturning point is surprisingly similar to these two vastly different phenomena, in which swinging is an intrinsic aspect of motion.
Is there chaos?
Although the motion of falling objects can be random – try dropping a playing card or business card from a height into a waste-paper basket – is it truly chaotic? In other words is the motion highly sensitive to the initial conditions?
Several researchers have found evidence of chaos in the motion of objects in fluids. In 1993 Hassan Aref and Scott Jones from the University of Illinois studied a very general 2-D theoretical model for asymmetrical objects moving through a zero viscosity or “inviscid” fluid in which vortices are not present. Chaos was also seen in the model of Tanabe and Kaneko that did involve viscosity but not vortices.
Although Stuart Field of Colorado State University, Franco Nori of the University of Michigan and co-workers recently reported the first experimental observation of chaos in a study of falling 3-D objects, we were unable to determine conclusively if the trajectories of our strips were chaotic. In our 2-D experiment, the range of parameters where chaotic motion occurred, if it occurred at all, was minimal and localized at the transition from flutter to tumble. A tumbling strip near the transition suddenly fails to complete a full rotation, and experiences an apparently random transition to the flutter regime for one cycle. This changes the direction of tumbling, and we had a few instances where tumbling strips randomly changed direction on one or two tumbles (out of about ten).
Our experimental approach to falling objects borrows more from condensed-matter physics and bifurcation theory: we think of flutter and tumble as two dynamic states, with a transition from one to the other. This transition is controlled by the Froude number. Above the “critical” value of 0.67 the object tumbles, and below this value it flutters. In our experiments, the Froude number is proportional to the square root of the mass and inversely proportional to the length of the strip. The thickness and width are kept constant, although the width also affects the Froude number. Thus longer or lighter strips, which have a lower Froude number, will flutter, whereas shorter or heavier strips, which have a higher Froude number, will tumble.
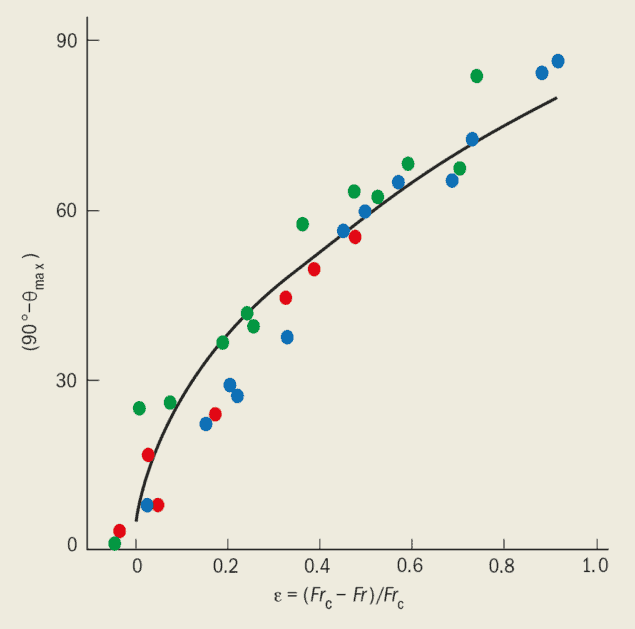
But what is the order parameter that quantifies the amount of flutter? The motion of the strip itself suggested the order parameter that we should use. During flutter, the strip oscillates from left to right, and rotates up to a maximum angle, qmax, at each extremity of its swing. No flutter corresponds to a maximum angle of zero. Our experiment showed that *max increases monotonically as the Froude number increases (figure 4). What happens when qmax reaches 90°? This would correspond to a sharply swinging strip, at the point where it could flip end-over-end. We found that our strips did this for Froude numbers just above the “critical” value of 0.67. For comparison, a strip of stationery paper (with a density of 80 g m-2) that is constrained to fall in 2-D would have this critical Froude number if it were about 18 cm long. Thus a standard A4 sheet (which is nearly 30 cm long) should flutter, ignoring its flexibility.
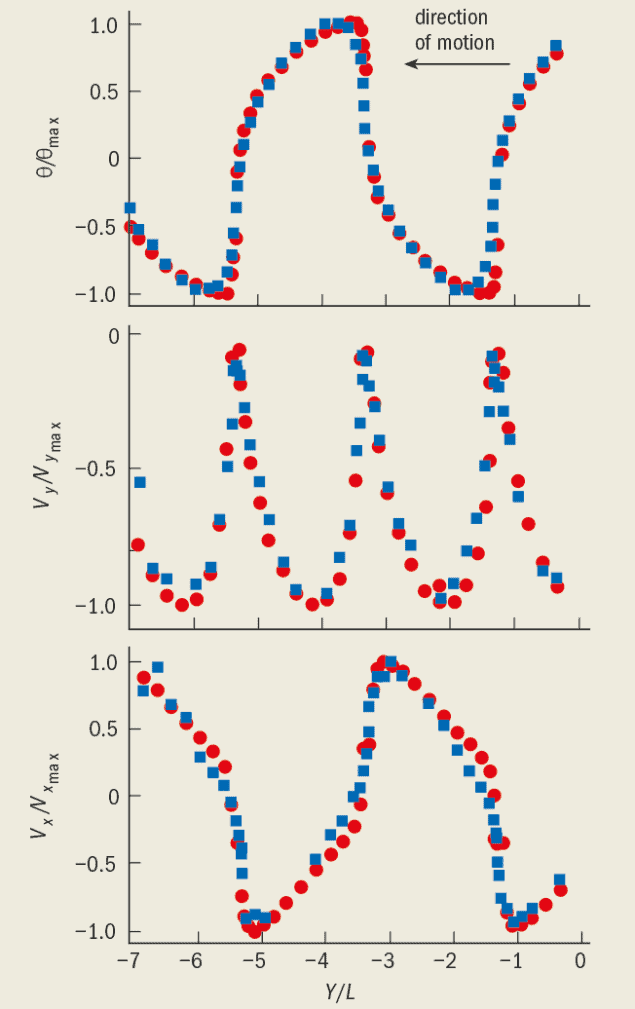
We compared our experimental data with a revised version of Kaneko’s model in which we replaced the viscous drag with inertial drag in the equations. This simple change normalizes the equations so that the Froude number appears as the only dimensionless control parameter in the model, a fact that agrees well with our experiment (figure 5). What the simulation cannot model is the formation of a vortex. From the video images, we have seen that vortices are produced near the centre of the strip when it is practically horizontal. Then, the strip tilts and the vortex slides along it towards the rising edge, growing as it does so. When the strip reaches its peak angle, the vortex is shed and the strip almost stops momentarily before reversing its direction. By incorporating the creation of vortices into the model, one could hope to capture even these more detailed aspects of the dynamics.
Falling through fluids is an everyday occurrence, yet one that brings out complicated and intricate dynamics that have defied a proper theoretical treatment for centuries. An explanation of this puzzling motion is rooted in fluid dynamics where the creation and shedding of vortices by the object is intrinsic to its motion. We have made progress towards understanding the basic ingredients governing the dynamics by simplifying the problem to 2-D. Our work may eventually lead to an understanding of the problem in 3-D and the role of vortices.
In the meantime, simplified approaches prove their worth and provide us with physical insight into the essentials of flutter and tumble.
- The authors would like to thank Hagai Eisenberg, Jay Fineberg, Jean-Marc Flesselles and Franco Nori for useful comments.