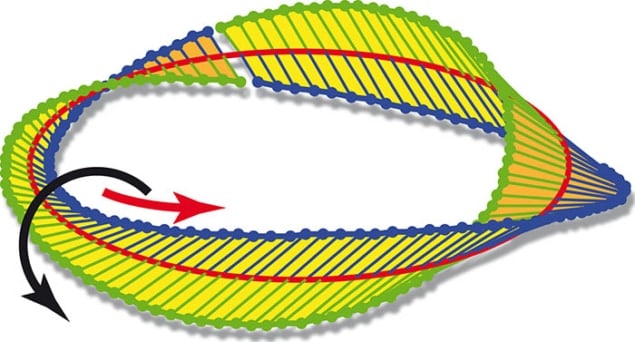
Möbius strips can easily be made at home – just take a strip of paper, give it a half-twist and then join its ends together. Trivial as it may sound, this loop possesses the unusual property of having only one surface and one edge. They also appear very rarely in nature and had never before been seen in light. Now, an international group of physicists has created such shapes using the polarization of laser light, and the researchers say that these electromagnetic patterns could be used to build new kinds of small-scale structure such as metamaterials.
The possibility of making an optical Möbius strip was suggested in 2005 by Isaac Freund of Bar-Ilan University in Israel. Freund calculated that a pair of laser beams could be manipulated such that the axis along which their combined electric fields oscillates – the polarization vector – would trace out a Möbius strip. He proposed using beams with different spin and orbital angular momenta, and making them interfere at specific angles to one another. The spin – or circular polarization – of an electromagnetic wave involves its polarization rotating clockwise or anticlockwise in a circle that is normal to the direction of propagation. Orbital angular momentum, on the other hand, comes from the twisting of a beam’s wavefront around its propagation axis.
Longitudinal challenge
Normally, a light wave vibrates in a plane at right angles to its direction of travel; but crucial to creating a 3D optical pattern such as a Möbius strip is to ensure that it also has a longitudinal component along the propagation axis. It turns out that Freund’s proposal for creating this longitudinal component is extremely challenging from an experimental point of view, so in this latest work Peter Banzer of the Max Planck Institute for the Science of Light in Erlangen and colleagues in Germany, Canada, Italy and the US have taken a different approach.
Banzer and colleagues used a liquid-crystal device known as a q-plate. When exposed to a beam with a certain spin, a q-plate transforms that beam so that it has opposite spin and 2q units of orbital angular momentum, where q can be any half-integer value and is a property of the particular plate used. The team used a green laser beam that was a superposition of two waves with opposing spin. The result was a beam with a polarization that varied across its width. It was circularly polarized at its centre, but linearly polarized – and with varying orientations of the polarization vector – further out.
Tight focusing
To extend this 2D pattern of polarizations into the third dimension, the researchers sent the beam through a tight-focusing microscope lens. This gave the beam a longitudinal component – the size of which depended on the degree of focusing. The result was a Möbius strip of polarization that measured just 200–250 nm across. By changing the q-plate, the researchers were able to create Möbius strips with three (q = –1/2) and five half turns (q = –3/2).
“It was a puzzle in the community as to whether such a topology could exist physically or whether it was just a mathematical description,” says group member Ebrahim Karimi of the University of Ottawa. “But now we have seen this in the lab, we know that Freund’s theory is correct.”
A brilliant tour de force at the cutting edge of optical technology
Isaac Freund of Bar-Ilan University
Freund himself describes the latest work as “a brilliant tour de force at the cutting edge of optical technology”, and says that it “goes far beyond verifying a particular prediction because it demonstrates that it is possible to measure the full 3D polarization structure of light”. It is a breakthrough, he adds, that is sure to be followed by research on other 3D optical systems.
Topological richness
Others in the field also praise the experiment. Michael Berry of the University of Bristol says that the work required “virtuoso mastery” of several optical techniques and that it “emphasizes Freund’s prediction of the geometrical and topological richness hidden in the laws of electromagnetism and expressible in light”. Miles Padgett of the University of Glasgow, meanwhile, says that the results may have important applications in areas such as optical lithography and nanofabrication.
One potential application is creating tiny 3D objects with unusual topologies – including tiny Möbius strips – which are very difficult to make using conventional lithography because of a lack of control over a light beam’s longitudinal component. Karimi told physicsworld.com that the new technique might be particularly useful for manipulating polymers, given the strong response that these materials have to light polarization. He also believes that the scheme might prove useful in building metamaterials – artificial materials that have unusual optical properties that can be put to work in optical devices.
The research is reported in Science.
- Check out our free-to-read digital edition of Physics World magazine containing 10 of our best-ever features on the science and applications of light, which we have put together to mark the International Year of Light



