In the years following his hugely successful book The Emperor’s New Mind, in which he argued that there is a quantum aspect to human consciousness, Roger Penrose has acquired a reputation among his peers for writing beautiful books that advocate controversial ideas. His latest book, Cycles of Time, is no exception. Its central idea is that one universe follows another in eternal recurrence on the grandest scale, and Penrose himself alerts the reader in his prologue (and epilogue) that this is a little crazy. However, the amazing facts revealed in quantum mechanics have turned “crazy” into an almost positive rather than pejorative epithet in physics, so perhaps the “health warning” should be taken with a pinch of salt.

Anyone who has heard Penrose’s recent lectures will have noted his passionate enthusiasm for his new idea. It came to him in the summer of 2005, when he was “depressing himself” by thinking of the wastes of time that stretch ahead of the universe according to the latest cosmological observations, which suggest an ever-accelerating expansion. He asked “Who will be around then to be bored by this apparent overpowering eventual tedium?” A thought occurred. If, by then, only massless particles are present (the rest having decayed), Penrose reasoned that eternity will pass in a flash since no proper time elapses at all for these voyagers along space-time light-cones. More significantly, it would mean that in the very distant future, the universe must have a particular structure much simpler than it would were massive particles present as well.

This idea, in turn, prompted Penrose to relate his decades-old ideas about the second law of thermodynamics to the geometrical structure of space-time that is implied by the observed accelerated expansion. Here, a quick primer may not go amiss. Einstein’s general theory of relativity is based on the curved, non-Euclidean geometry that Riemann introduced in 1854. This geometry has a part that describes measured angles (known as the “conformal geometry”) and a conceptually distinct part that describes distances. The point to understand about this is that angles, not distances, are what matter in determining the shape of something. One can, for example, imagine shrinking or magnifying the sides of a triangle, making it larger or smaller, while leaving the shape-determining angles unchanged.

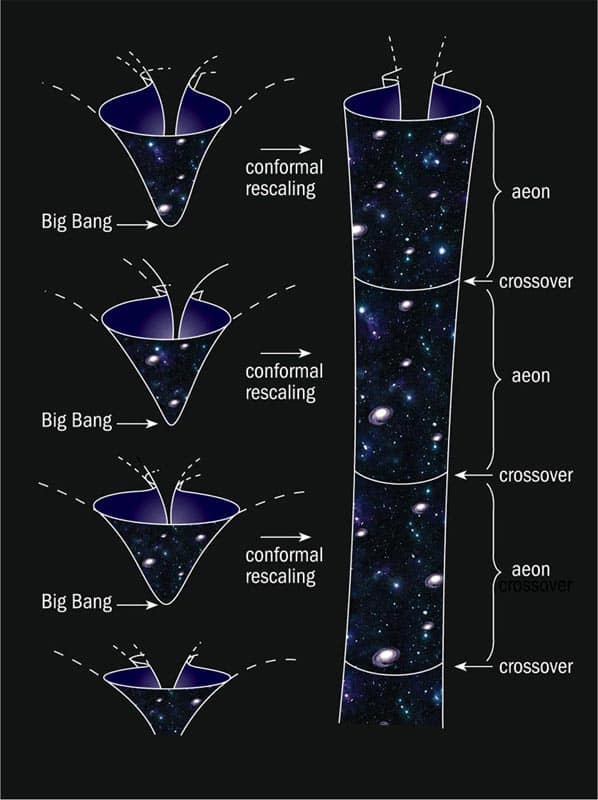
From about 1962 Penrose introduced a similar device into general relativity, but with a further twist that allowed him to be able to “blow up” the Big Bang and black-hole singularities, where spatial distances shrink to nothing but matter densities and space–time curvatures become infinitely large. As he explains, his conformal, or angle-preserving, diagrams “bring into our finite comprehension the infinite regions of space and time” and fold out “those regions that are infinite in a different sense, namely the space-time singularities”. These diagrams have become an indispensable tool for relativists and play a key role in Penrose’s book. They can be used to depict the most salient features in space–time – in particular the violent singularities just mentioned, but also regions infinitely far away in space or time.

Above all, Penrose is concerned with the structure of our universe at its birth and in its very distant future. There is much evidence that suggests that its structure is “spacelike” at both extremes. This means that, in their essence, the “ends” of the universe are like our ordinary 3D space at a given instant of time. They may, however, have infinite curvatures – a spacelike singularity – or, alternatively, they may be blandly smooth.

Now we come to the second law, the hugely enigmatic nature of which Penrose has been emphasizing for decades. As he characterizes it, the Big Bang was a spacelike singularity with a conformal geometry that was utterly, improbably smooth compared with what one might reasonably expect. In contrast, the remaining part of the geometry – the one concerned with distances – was highly singular, since all distances shrink to nothing as one goes back in time to the Big Bang. Penrose’s preferred precise mathematical formulation of this state of affairs is down to his collaborator Paul Tod. According to it, one can in imagination extend our space–time beyond the Big Bang in a smooth, conformal manner.

You may still wonder what all this has to do with entropy and the second law of thermodynamics. Well, from the point of view of gravitational physics, the incredibly smooth conformal geometry at the Big Bang corresponds to very high order and extraordinarily low entropy. We and all the other increasingly intricate structures in the universe have been living off that order ever since. But how did this order get there? That was Penrose’s conundrum.

Penrose’s new inspiration came when he realized that the positive cosmological constant that is accelerating the universe’s expansion means that, from the conformal point of view, the universe will be spacelike at its end. Since the Big Bang singularity is also spacelike, it might be possible, provided certain conditions are satisfied, to match conformally the whimpering end of our universe to its explosive beginning. Their shapes could then dovetail, not just mathematically but in physical reality. However, Penrose rejected this “biting its tail” possibility on the grounds that it would introduce paradoxes of the “go back in time to kill your grandfather” variety and instead opted for what he calls a conformal cyclic cosmology. Here, one aeon succeeds another at a spacelike “crossover”, at which both universes’ conformal geometries – but not their scales – match. This process can be repeated eternally.

There are numerous problems to be overcome in this proposal, which involves a radical rethinking of Penrose’s own ideas about the second law. One serious difficulty is that it relies heavily on all particle masses, including that of the electron, becoming exactly zero in the very distant future. Many particle physicists will question that. But the biggest difficulty of all is that even if the shapes of the aeons match, how does the transition from an infinitely large scale before crossover to an infinitely small scale after crossover occur? This is where the argumentation and mathematics get tough.

Penrose effects the crossover with a scalar field dubbed “phantom” before the crossover, because it involves a purely mathematical conformal transformation. This field then becomes physical after crossover, and Penrose tentatively identifies it with the dark matter needed to explain the structure of galaxies and clusters of galaxies. Although the scalar field evolves deterministically, and in that respect is conventional, its transformation “at once” from being a purely mathematical object to a physical one has no parallel elsewhere in physics – unless one likens it to the notorious collapse of the wavefunction in quantum mechanics.

I have to say that the key idea strikes me as not so much crazy as implausible. Nevertheless, I think many people will, like me, be glad to have read this book. Penrose’s prose is wonderfully clear and concise (I admit to envy), and the “intelligent layreaders” who buy his books in such remarkable numbers despite all his equations will be stimulated by his lucid (and largely equation-free) discussion of the second law. Budding relativists will get an excellent introduction to conformal diagrams and much else. And I am sure sceptics will enjoy looking for defects in the arguments.

Let me end provocatively, like Penrose, for I share his fascination with conformal geometry. In one sense, I wish he had been more radical. Despite his great attraction to conformal geometry, Penrose still accords length a real physical role. But in fact we only ever observe angles, never lengths as such. Do we really need them?