What do earthquakes, robotics and jumpers have in common? Samuel Poincloux explains why the answer lies with knitting – and how stretching a knitted material is rooted in mechanics
If you’ve ever done a PhD in physics, you’ll know you usually begin by ploughing through lots of background reading, learning how to use your lab’s equipment and maybe even carrying out some provisional experiments. My PhD was a bit different. I started off watching YouTube videos to improve my needlework.
The project I had accepted at the Ecole Normale Supérieure in Paris was about the mechanics of knitted fabrics. The research was to have two sides: a theoretical one to determine what equations described the system; and an experimental one to mechanically test actual knits to guide and verify the theory. The trouble was, I barely knew what a knit was when I accepted the project.
I quickly learnt that there are differences – both structural and mechanical – between a knit (such as a jumper, scarf or hat) and a weave (such as a table cloth, shirt or pair of jeans). In fact, those differences are easy to demonstrate. If you pull on your jeans, you should notice that the weave hardly deforms. Pull on a knitted jumper, in contrast, and it can be effortlessly elongated by up to two times its length. The stretchiness of a knit is also obvious if you wrap it around something: by locally stretching, a knit can fit complex shapes; a woven fabric, however, has to fold to conform to it.
The discrepancies between knits and weaves are true even if they are made of the same yarn. That’s because it is the structure of how the yarn is interlaced that dictates the mechanical behaviour, not the precise composition of the material. As I soon learned in my PhD, a woven fabric is made from two bundles of yarns that intertwine perpendicularly (figure 1a). Pulling on a weave is therefore not very different to pulling on a single yarn.
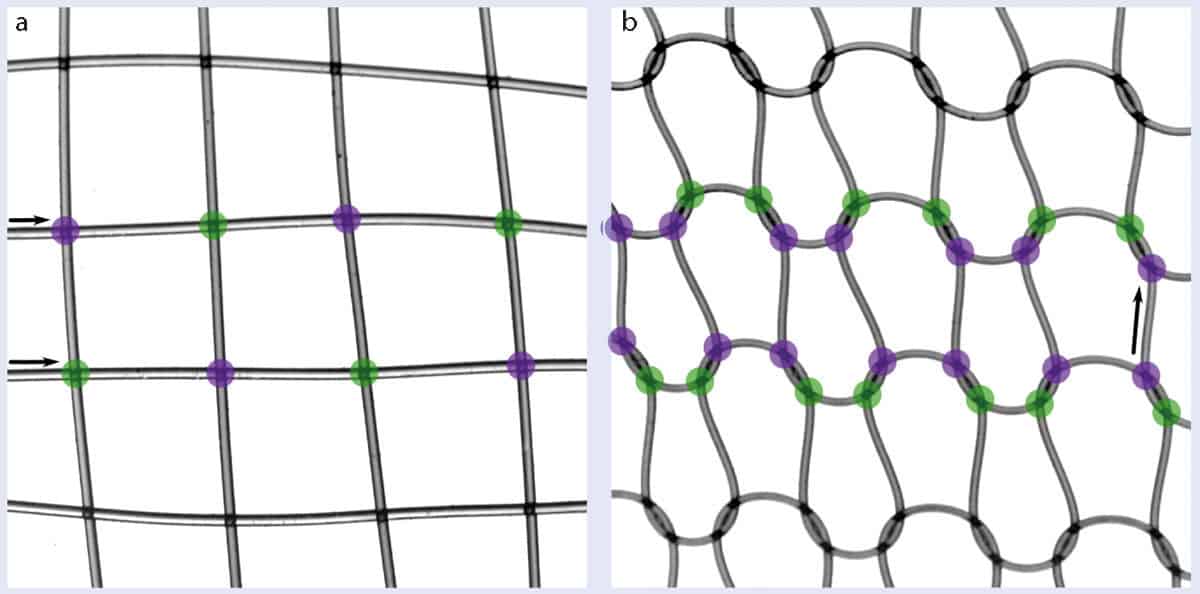
Knitted fabrics, however, are generally made from a single yarn shaped into a network of loops called stitches (figure 1b). Pulling a knit is therefore equivalent to deforming loops and not directly pulling on the yarn itself. This mechanism illustrates how different interlacing structures can affect the mechanics of a textile.
Knit science
I should make it clear that my fellow researchers and I were not the first people to wonder how a knit deforms. Anyone knitting for fun needs a profound empirical knowledge of knit structure and mechanics. A knowledge of knits is also important in industry – and not just for the clothing sector. It can, for example, be used to reinforce composites in planes, cars or trains.
The first studies of knit mechanics began in the 1960s. Inspired by mechanical engineers, the research involved modelling the exact path of a yarn in a stitch to determine how this yarn deformed if slightly pulled. This work provided some beautiful equations, but they described just one stitch and not a whole fabric.
More recent studies were encouraged by the graphics community, which might seem odd, but animated characters must be dressed properly too. This work led to a fully numerical approach (ACM Transactions on Graphics 31 4), which starts from the yarn and goes up to the whole knit. It provided very realistic mechanics, but did not give an analytical expression of the fabrics’ mechanical constants, nor reveal the interplay between structural parameters (for example, size of stitch) and material parameters (such as the rigidity of the yarn).
My PhD therefore involved looking between these two extremes, where there’s a gap in our understanding. I wanted to find out if we can get equations to directly describe the mechanics of a whole fabric while at the same time defining the role of the individual parameters.
Knitting like a physicist
Two major issues arose early on in my quest to get answers. First, despite the YouTube tutorials and some precious advice from my grandmother, my early knits were terrible and useless for proper testing. The second problem was that the number of parameters in commonly used knits is colossal because even the most standard yarns are themselves incredibly complicated objects.
Despite the YouTube tutorials and some precious advice from my grandmother, my early knits were terrible and useless for testing
To tackle my lack of knitting skills, I contacted staff at a nearby art school, which luckily had a workshop with manual knitting machines and looms. More importantly, the head of the workshop kindly agreed to teach me how to craft the perfect knit. With this knowledge – and a 40-year-old, second-hand domestic knitting machine we bought for the lab – I was now able to make experiment-worthy knits.
To deal with the second problem – the complexity of the knit – we did what all physicists love to do: we simplified the system as much as possible so that only the essential parameters remained. We knew that what defines a knit is the pattern of the crossing points, so we began by picking the simplest yarn we could find – nylon fishing lines. Then, we made a very loose knit so the yarn did not get too deformed. Though a bit daring to be a garment, the resulting knit (similar to that in figure 1b) is a wonderful system for a physicist to play with. It means we only have to take into account a few factors (which may include several numerical parameters): the elasticity of the yarn, the structure imposed by the interlacing pattern and yarn–yarn friction at the crossing points.
Elasticity and tremors
We finally had a knit we could do experiments on. To assess its mechanical response, we measured the force needed to pull the knit and took pictures to evaluate how it locally deformed. The results were not as simple as we expected.
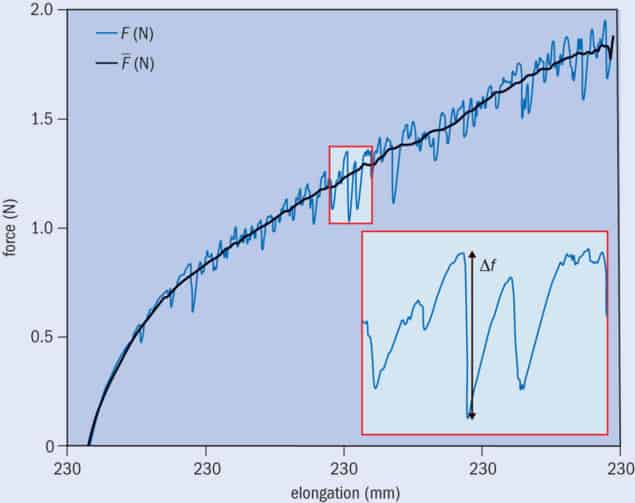
The mechanical response (figure 2) had two features – one elastic and the other noisy. The elastic element could be identified because of how it repeats with the stretching cycles, and it therefore was predictable. The noisy response – which warped the elastic one by small perturbations – was not identical over cycles and so had to be considered from a statistical perspective. By simplifying things in this way, we could easily spot the culprits for each response.
The elasticity of a fabric naturally derives from the yarn elasticity and the periodic looping stitches, so we need to define how these factors interplay. This means predicting how the elastic energy of the yarn varies as the knit is deformed.
Instead of basing the model on the yarn itself, as in standard mechanical studies, we looked at it as a network of subunits, or stitches. This approach makes the problem much simpler since one stitch is characterized only by the distance and orientation of its neighbouring stitches, not by the full path of the yarn. The tricky bit is to express the energy of the yarn as a function of the stitch dimensions.
In our simplified knit, the yarn deforms when it bends because stretching is much more energetically costly. The loop geometry of a stitch means that the curvature of the yarn is tightly linked to loop dimensions. As a stitch gets smaller, the bending energy increases, providing a simple relationship between energy and the network parameters. However, no stretching implies that the yarn is inextensible, a constraint we also have to express. Again, the link between the length of yarn in a stitch and the stitch dimensions is direct. If a loop expands in all directions, the yarn’s length must increase. So if the yarn is inextensible, loop expansion in one direction must be compensated for by a shrinking in a different direction.
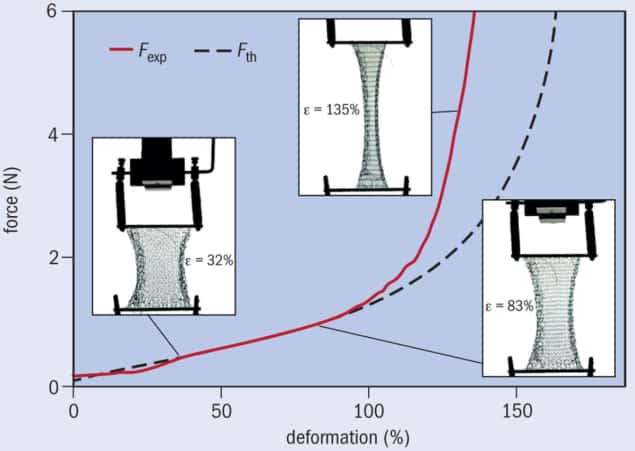
Using these ideas, we obtained a mathematical formula giving the mechanical response of one stitch, and therefore also for a knit where all the stitches are deformed identically. The model perfectly captures the observed elastic response of a knit being pulled (figure 3), even when the knit is stretched to twice the initial size. At further elongations, however, stitches cannot laterally shrink any more because of the finite yarn diameter. The yarn then stretches and compresses – factors that are not taken into account in the model, which therefore underestimates the pulling force. To predict more realistic cases where deformation is inhomogeneous, we can keep the same approach but we have an additional constraint: stitches must keep the same neighbours (Physical Review X 8 021075).
Crackling the knits
Let’s now look at the noisy part of the response in figure 2. By zooming in on the force curve, we notice that the fluctuations follow a very specific shape: a slow linear increase interrupted by an abrupt drop. We know that this behaviour was not due to the limitations of our equipment because it was up to 100 times larger than the precision of the experiment. Instead it can be explained by the fact that when one object is pushed along the surface of another, friction resists the pushing force. Below a critical force, friction dominates and the two objects stick together; above this force, however, the push overcomes the friction and the objects begin to slide across each other.
This phenomenon appears at each crossing point in our knit. As you pull it, the contacts will suddenly slide when the critical force is reached and the friction is overcome. That’s why you get the slowly increasing force, interrupted by the sliding-induced plunges.
The drops have many different sizes, meaning that the contacts don’t slide one by one but slip in groups. Indeed, contacts are not isolated from each other since they are linked by the elastic yarn.
To characterize all those events we first needed to look at statistical quantities such as the probability distribution of the drops’ amplitude (Δf). It turns out that there are lots of small drops but few big ones, following a power-law distribution (Phys. Rev. Lett. 121 058002). One feature of this law is scale invariance, which means that some event properties are independent of their size. To illustrate this effect in the distribution, we can simply zoom in on a small portion of the curve and see that the size of the corresponding events cannot be distinguished anymore: the decreased rate remains constant.
This property is characteristic of so-called crackling noise – an intermittent response displayed by lots of systems that exhibit sudden events when being slowly loaded. The most widely studied example is the Earth’s crust. When two tectonic plates (such as the Pacific Plate and the North American Plate) rub against each other while travelling in opposite directions, they slowly build up energy while trying to overcome friction, but will then suddenly shift, resulting in an earthquake. The probability distribution of the earthquake’s size, known as the Gutenberg–Richter law, shows the same features as those measured in our knit.
Earthquakes, robots and jumpers
From structural mechanics to earthquake-like statistics, the physics behind pulling a knit is very rich. While understanding the elasticity of knits may help scientists find direct applications in composite reinforcement, soft robotics or architecture, comprehending the statistical part may help fundamental physicists understand why such different systems show similar behaviour.
By simplifying the knits, we have managed to isolate and understand different mechanisms that might otherwise be hiding behind other complex phenomena in standard knits. But we have to be careful to not oversimplify – for instance, if we had completely got rid of friction, as we initially planned to, we would have missed the crackling phenomenon.
Now my PhD is done, the next stage in this research is to add complexity, step by step and in a controlled way, by changing the knit pattern or the yarn properties. Maybe by the time we unravel all the intricacies of knitting, I may even have learnt how to knit a sweater for my grandmother.




