The combination of quantum mechanics and game theory promises to improve the odds of winning and may provide new insight into novel physics

Whether we want to or not, we all play games – and not just at Christmas. Every day we face situations that require us to make the best decision based on our knowledge and past experience. The trouble is that our information is often incomplete, situations change, and – worse still – there may be hundreds of other people trying to do the same thing. Many aspects of life, such as trying to find a seat on a train or playing the stock market, can be viewed as a competitive game that we repeatedly try to “win”. There are also many situations where it is better to co-operate, for instance at work or in a sports team.
Game theory provides a way of dealing with very simple forms of such games. In general, these theoretical approaches consider so-called static games without any repetition or learning from the past. They also contain just a limited number of players, all of whom have access to the same strategies.
Game theory is not new: back in 1928 the Hungarian mathematician John von Neumann published the fundamental theorem of “zero-sum” games in which one player’s loss is equal to the second player’s gain. He went on to co-author Theory of Games and Economic Behaviour with Oscar Morgenstern in 1944, and in so doing formally gave birth to the field of game theory. Since then applications have been considered in fields as diverse as military warfare (in particular during the Cold War, when there were only two major players), anthropology, social psychology, economics, politics, business and philosophy.
Most applications in science have focused on biology at the macroscopic scale – in particular the competition and co-operation between “players” at the level of species or individual animals. However, Paul Turner and Lin Chao at the University of Maryland recently made the exciting discovery that an RNA virus – a primitive yet fundamental microbiological structure – may also engage in simple two-player games. This finding prompts the question: could there be a more fundamental connection between basic science and games?
Playing with games
Game theory has recently made it big in Hollywood with the movie A Beautiful Mind, which charts the tortured life of Nobel-prize-winning mathematician and economist John Nash. But to understand why Nash’s work is so important, we first need to understand what is meant by a game. In classical game theory, a game consists of a set of players, a set of strategies that dictate what actions a player can take, and a “pay-off function” that specifies the reward for a given set of strategy choices. A reward could be monetary or more spiritual, such as an increase in happiness. The corresponding pay-off to each player is represented by a numerical value. If you are one of the players, the aim is, of course, to optimize your own pay-off. However, if everyone else is trying to do the same, how should each player actually play the game?
Enter John Nash: he proved that every static game with a finite set of strategies for each player has at least one equilibrium. This “Nash equilibrium” is the set of strategic choices that provides the optimal pay-off for both players – in which no player can do better by changing their strategy while the other player’s strategy remains unchanged.
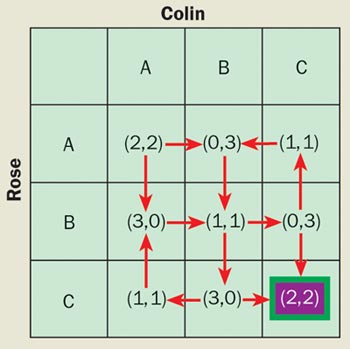
Game theory would have been perfect if only every game had a unique Nash equilibrium. However, the world is more interesting than that. Although certainly beautiful, Nash’s work does not show us how to compute such an equilibrium, nor does it indicate how many such equilibria exist. Even very simple games can possess multiple Nash equilibria and there are no general tools for singling out any particular one. Figure 1 illustrates the problem for a non-zero-sum game with two players. How will the players ever know which equilibrium to aim for? If both players make a decision in an attempt to maximize their own pay-off, then they may end up with the worst outcome for both.
Figure 2 illustrates a further problem with such classical games: even if they choose a strategy that corresponds to a Nash equilibrium, the two players may actually squander a far larger pay-off. This is the case in the famous “prisoner’s dilemma”. In this game, we imagine that two people have been arrested on suspicion of having jointly committed a crime. The suspects are placed in separate rooms for questioning, without being able to communicate with one another. If one of them confesses to the police while the other remains silent, then the one who defects (i.e. confesses) will be freed while the one who remained silent is sentenced to three years in prison; if each betrays the other by defecting, both will be sentenced to two years in prison. However, if both suspects remain silent, they will effectively be co-operating with each other against the police: both will then get away with just one year in prison.
In the prisoner’s dilemma, the Nash equilibrium is when both suspects defect by confessing, even though the situation in which they both co-operate against the police by remaining silent yields a better pay-off for each player. As shown in figure 2, if we interpret pay-offs as energy gains, it is possible to illustrate the prisoner’s dilemma in terms of a simple physical model for two electrons in the electronic shells of an atom.
So do games have anything deeper to say about physics, or vice versa? Maybe. Most surprisingly, the connection might arise at the most fundamental level of all: quantum physics. Let’s start with some circumstantial evidence. As well as being the father of game theory, von Neumann also made seminal contributions to the fields of quantum mechanics and computation. Furthermore, an experiment in physics can arguably be viewed as a “game” against nature in which the observer tries to maximize the informational output while nature evolves relentlessly toward increased disorder (entropy). In short, the common link with physics is information: games, quantum mechanics, computation and, ultimately, physics are all concerned with information. So what would happen if we combined quantum mechanics with games? This idea occurred to David Meyer of the University of California at San Diego, and in 1999 he initiated the study of quantum games.
Profiting from a quantum edge
The story starts with Captain Picard’s showdown with Q on the bridge of the Starship Enterprise. Meyer imagined both Star Trek characters playing a coin-flipping game as follows. Q has a coin, which he prepares and gives to Captain Picard; Picard can either flip the coin or leave it unchanged before handing it back to Q. Before they both look at the outcome, Q is allowed to flip the coin again if he wants to, but he does not have to. Picard loses if the final outcome is heads, but wins if it is tails. However, Q is allowed to use “quantum strategies” while playing the game whereas Picard is restricted to classical strategies. To Picard’s dismay, and to the detriment of the entire galaxy, Q manages to win every time because he can exploit these quantum strategies to his advantage.
To see how Q wins we must replace the classical coin – which can be in one of only two states – with a quantum coin that can be in an infinite number of states. For instance, we can think of the quantum coin as the spin of an electron: we can define heads as the spin pointing along the +z axis and tails as the spin pointing along the –z axis. However, the spin can also point along the x or y axes.
Captain Picard can only perform the classical action of flipping the spin – which is equivalent to rotating the spin about the x axis – or not flipping the spin. However, Q can perform a whole range of quantum operations. For instance, he can use a so-called Hadamard operation to prepare the spin so that it is pointing along the +x axis. This means that if Picard flips the spin about the x axis, it will still point in the +x direction; and if he does not flip the spin, it will obviously remain pointing in the same direction. Once Picard completes his move and returns the spin to Q, the latter can simply rotate the spin so that is pointing along the +z axis (i.e. heads) and win the game.
Loosely speaking, we can say that Q wins by using quantum mechanics to prepare the coin in a state that is both heads and tails at the same time – which is like saying that the classical coin is standing on its edge – and that Picard always loses because he is unable to change this state by flipping the coin.
Steven van Enk at the California Institute of Technology later showed that Meyer’s Star Trek game could be simulated classically and is therefore not purely quantum mechanical. But this did not stop many researchers from diving into the new field that Meyer had created.
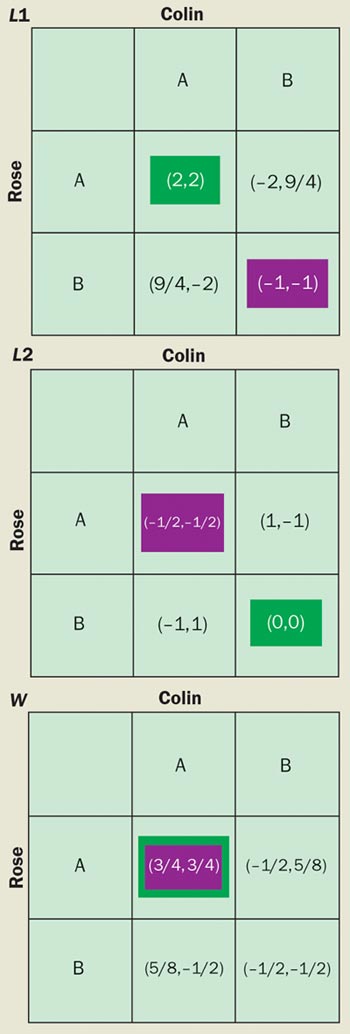
In the same year, Jens Eisert, Martin Wilkens and Marcus Lewenstein at the University of Potsdam in Germany proposed a quantized version of the prisoner’s dilemma game (figure 3). They claimed that the resulting game possessed a unique Nash equilibrium that also yielded the maximum possible pay-offs – the game was said to be “Pareto optimal”, a concept invented by the Italian economist Vilfredo Pareto. The players in the quantum game apparently managed to resolve the prisoner’s dilemma!
This particular conclusion was later criticized by Simon Benjamin and Patrick Hayden of Oxford University on the grounds that the quantum strategies considered were limited in an unphysical way. However, the theoretical framework introduced by Eisert and co-workers is unaffected by this criticism and, in addition, underlies most of the subsequent research in quantum games. We will therefore discuss the underlying idea in more detail.
Quantum dilemma
Playing a game boils down to performing an action: this action is based on a strategy that is chosen after the players consider the pay-offs. We can imagine the existence of a referee whose sole aim is to collate the actions of the players and then to compute the pay-offs. These actions may be encoded as numbers – for example in the prisoner’s dilemma game of figure 2, the players use the value “0” to represent their decision to co-operate (strategy A) and “1” to represent their decision to defect (strategy B).
We can therefore think of the referee initially producing two coins, each with 0 on one side and 1 on the other. The referee then passes one coin in the 0 state to each player (i.e. with 0 facing up). The players then decide whether to return the coin unchanged – and hence co-operate with each other – or to flip the coin to yield the value 1 and hence defect. The game is therefore equivalent to one in which the referee issues pairs of binary coins or “bits”.
In the quantum version of this game, the referee issues qubits rather than bits. A qubit is a two-level quantum system, such as the spin of an electron or the ground state and excited state of an atom. Continuing with the prisoner’s dilemma game as an example, the referee passes a qubit to each player (figure 4). Two qubits are therefore involved in the quantum prisoner’s dilemma game, as opposed to the single qubit (i.e. single coin) used in Meyer’s Star Trek game.
The referee can exploit the full weirdness of quantum mechanics by “entangling” both qubits before giving them to the players. Entanglement is a purely quantum effect that many physicists believe is the essential ingredient for unleashing the potential power of quantum information processing and quantum cryptography – indeed Albert Einstein considered entanglement to lie at the heart of the fundamental “spookiness” of quantum mechanics.
To render the prisoner’s dilemma game quantum mechanical, we have to entangle the two qubits. When two qubits are entangled, we mean that they are linked or correlated in a highly complex way. For instance, it is possible to create pairs of photons that have their polarizations entangled: if the first photon is circularly polarized in a right-handed sense, then the second photon is polarized in a left-handed sense, and vice versa. In the quantum version of the prisoner’s dilemma, flipping one qubit is equivalent to flipping the other qubit while leaving the first one unchanged. Indeed the distinction between the two qubits becomes so blurred that they are no longer identifiable as individual objects. This strange but powerful correlation is purely quantum mechanical, and may be harnessed to co-ordinate an improved pay-off. (To achieve the same results classically would require the players to somehow cheat, thereby rendering the game non-competitive.)
The players act on their individual qubits using any available quantum operation. Leaving the qubit unchanged corresponds to the identity operator I, while flipping the qubit corresponds to the Pauli spin operator X. In addition there are an infinite number of other quantum operations. To visualize this concept, think of a pencil held at one end, which is free to rotate through any angle in three dimensions. The pencil represents heads when it points vertically up, and tails when it points vertically down. When the pencil is horizontal, it represents an unphysical state for a classical bit (like a coin on its side) but this is a perfectly acceptable quantum-superposition state. The player can therefore be co-operating and defecting at the same time.
At the end of the game the referee collects the final state of the two qubits. First the referee “undoes” the initial entanglement operation, in order to avoid introducing any bias into the quantum game with respect to the classical version, and then measures the final state to determine the players’ pay-offs. In principle, the resulting pay-off can be higher than in the classical game (see figure 3). Remarkably, Jiangfeng Du and collaborators at the University of Science and Technology of China in Hefei have recently demonstrated the quantum prisoner’s dilemma game experimentally using a nuclear-magnetic-resonance quantum computer.
Two’s company, three’s a crowd
Like most of quantum game theory to date, we have focused on two-player games. Following the controversy surrounding the search for a truly novel quantum advantage in such games, one of us (NFJ) conjectured that new phenomena should emerge for quantum games with three or more players. After all, the novel phenomenon of chaos in classical systems only appears for three or more particles. And there are special quantum systems that only exist for three or more electrons, such as the special states proposed by the Nobel laureate Robert Laughlin of Stanford University to explain the fractional quantum Hall effect.
In addition, numerical simulations on repeated classical games have shown that novel co-operative phenomena can arise in the many-player limit. An example of such a co-operative effect is a crash in a financial market, which occurs when a group of traders suddenly decides to sell at the same time.
Benjamin and Hayden took our conjecture seriously, and subsequently constructed a three-player version of the prisoner’s dilemma. Their game is equivalent to the two-player game except that the referee now gives and receives three qubits. Remarkably, the three-player game does indeed exhibit a novel coherent quantum state in which the pay-offs to the players are higher than anything that could be achieved classically. This superior outcome arises when one player co-operates, another defects and the final player does something quantum mechanical in between.
However, the problem of co-ordination still arises: in particular, two players have to accept a pay-off that – while larger than the classical result – is smaller than that of the third player. But in the absence of prior communication, how do the players decide who receives what? Roland Kay, also at Oxford, addressed this question by considering a repeated game. He allowed the players to evolve their strategy by choosing a new one from a fixed set of strategies if they found themselves losing too often. Kay’s work showed that one of the several possible coherent quantum states would be reached eventually.
All this assumes that the players have a reliable source of qubits, just like an unmarked deck of cards in a casino. But what happens if the deck is marked? Putting this in a physical context, one could imagine a “demon” who corrupts the supply of qubits but whose actions are unknown to the players (just like a corrupt croupier in a casino). Such a demon can be thought of as injecting noise into the system. One of us (NFJ) set up this model, and investigated the effect of noise within the three-player quantum game.
It turns out that the quantum advantage becomes a disadvantage above a critical value of the corruption rate or noise level. In particular, the coherent quantum effects impede the players to such an extent that the classical game outperforms the quantum game. Given a choice, the multiplayer system eventually does better if it adopts classical, rather than quantum, behaviour. The “optimal” choice of game therefore changes from quantum to classical as the noise level increases: the crossover occurs when the noise level corresponds to the energy separation of the two levels of the qubit.
Remarkably, this finding coincides with the physicist’s basic rule of thumb that classical phenomena supersede quantum effects when the temperature exceeds the relevant energy separation of quantum levels in a system. It also suggests that noisy quantum games may provide new insight into the physics of decoherence, which destroys the quantum-mechanical nature of fragile qubits.
In search of the killer application
First the bad news: in spite of the interesting results that have been achieved, there is a basic problem with most of the studies of quantum games to date. Whatever the quantum game does can usually be accounted for within classical game theory, simply by appealing to a more complicated game structure. This is because quantum games can ultimately be represented by a classical number of players, strategies and pay-offs – precisely the objects studied in classical game theory. Quantum games therefore do not appear conceptually different from their classical counterparts.
Now for the good news: although classical and quantum games fall under the dictum of classical game theory, we have recently shown that it can be more efficient to play quantum games. If we entangle the qubits shared between the players, then the players have a greater number of strategies to choose from than in classical games. In other words, less information needs to be exchanged in order to play the quantized versions of classical games. This improvement in efficiency alone makes the whole subject worth studying.
Apart from the issue of efficiency, quantum games may also be at work on a more fundamental level in nature. Game theorists have long realized that it does not take a perfectly rational being to recognize a “best strategy” and they have therefore applied their techniques to model the behaviour of both animals and bacteria. Quantum game theory may eventually provide the tools to help understand the interactions of fundamental particles or molecules if we treat them as individuals as in figure 2. Indeed some search algorithms – such as simulated annealing and adiabatic algorithms – may be seen as methods for persuading individual qubits to co-operate collectively in order to achieve the optimal global pay-off. Consequently, there is likely to be a strong connection between evolutionary games and games derived from the dynamics of physical systems.
In the computation community there is a widespread feeling that game-theoretic techniques provide the only general tools that can prove lower bounds in classical algorithms. For example, in tree-evaluation problems – in which the value on each leaf of the tree represents the input – we can view the algorithm designer and the input feeder as players in a zero-sum game. In particular, the designer is trying to minimize the running time of the algorithm while the feeder is trying to maximize it. The “minimax” theorem from classical game theory can hence provide us with a tight bound on the running time of any randomized algorithm that solves the tree-evaluation problem. A similar approach could provide some much needed insight for the case of quantum algorithms.
A particularly interesting application may arise from an effect that was recently discovered in classical games ( figure 4). To illustrate this so-called Parrondo effect, let’s take another look at the prisoner’s dilemma game. Randomly switching between two prisoner’s dilemma games in which the players “lose” should prompt the players to choose the Pareto optimal and thus increase their global gain (i.e. they now win). The Parrondo effect could even be applied to the design of quantum algorithms and to control qubit decoherence. In related work, Derek Abbott and Adrian Flitney of Adelaide University introduced a quantum Parrondo game within the Eisert scheme described earlier, while David Meyer has discussed a version with a so-called Brownian ratchet.
Going to the limit of very large numbers of particles, which is the case most commonly found in physical systems, leads us into the realm of many-player or many-agent games where each particle is treated as a player. Such games suggest that physics can add greater value to game theory, and vice versa. For example, consider political elections, which are a popular topic in game theory. Let’s assume that voters interact with each other just as electrons do in the well-known Ising model in statistical physics. The study of phase transitions has shown that infinitesimal changes in the initial conditions of a system can lead to large qualitative changes in the outcome. Hence a candidate who is ranked almost equal with his or her rival in a presidential election campaign could win overwhelmingly simply by seizing the additional support of one small town. The effect of quantum fluctuations on such phase transitions is an area of active study in physics, suggesting that the quantum version of many-voter games could also prove very fruitful.
Continuing in the realm of fundamental physics, we reiterate our belief that a deeper understanding of the relative advantage between classical and quantum many-player dynamical games may eventually shed some much-needed light on the connections between quantum and classical many-particle systems. It is possible that pay-offs could be used to represent energies, while the entangled state of the many-player quantum game could represent some exotic many-particle wavefunction. As discussed above, an external demon’s actions could then be used to mimic environmental decoherence. A related idea was recently presented by Roy Frieden of the University of Arizona. Frieden showed that physical laws can be derived by considering the information content of a physical quantity, implying that the process of making a measurement represents a game against nature. It turns out that the observer can never “win”, in the sense of obtaining complete information about a particular physical phenomenon. Instead, the phenomenon under study takes on an all-powerful, but malevolent, force – the information “demon” who is looking to increase the degree of “blur” of information, and against whom the observer is forced to play.
Outlook for quantum gaming
We have given a very brief overview of the recent birth of quantum game theory, and the extent to which physics and games are related. Quantum game theory is now a toddler: tantrums aside, it is likely to grow at a steady pace. Quantum games have superior efficiency compared with their classical counterparts. Moreover, their study may lead to a deeper understanding of quantum algorithms and quantum information processing, and could even shed light on the great divide between quantum and classical physics.
We believe that quantum game theory adds another perspective to physical problems. As Richard Feynman once said: “Physicists of any good should know six or seven different methods to solve the same problem”. There seems little harm in applying game theory on such occasions.
But to what extent will quantum game theory eventually say something novel about physics? Maybe it will turn out that nature, including physics, can in fact be viewed as just one big game that spans classical and quantum multiplayer systems. Such ideas are highly speculative, and being a researcher in such a fledgling field is clearly a big risk. But life is full of risks. And life, after all, is just a game.