Fill a narrow glass capillary tube with water, then turn it horizontal. Conventional wisdom says that the water will remain inside the tube. But a group of scientists in Spain and the UK has found that when the internal cross-section of the tube has a certain shape – triangular or a squashed ellipse – the tube will empty, however narrow it is. This phenomenon could represent a new way to control flow in microfluidics. It might even already be exploited in nature, for example in plants or blood vessels.
Innocent question
The authors of a new paper first began thinking about the behaviour of liquid in a horizontal capillary tube about eight years ago, when mathematician Carlos Rascón of the University Carlos III de Madrid, Spain, and theoretical physicist Andrew Parry of Imperial College London, UK visited Dirk Aarts at the University of Oxford, UK.
Aarts was experimenting on the behaviour of colloid–polymer mixtures in slit-like capillaries, and he commented that at the end of the day’s work they’d turn the capillaries horizontal and see the meniscus slump. He asked his visitors the innocent question “Do you know what shape it is?” And the trio realized that none of them knew how to work that out.
Keeping it simple
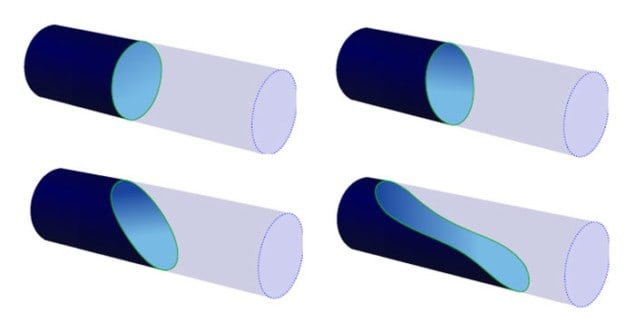
The equilibrium shape of the meniscus comes from minimizing the total free energy of the liquid confined by the solid walls of the tube. It can have a range of shapes, from a simple sloped meniscus, to an s-shaped cross-section in which a “tongue” of liquid extends along the base of a capillary.
The 3D shape is not easy to calculate and so, in 2012, the researchers’ first step was to calculate a reduced-dimension solution. They showed that for a simple 2D slit (with a 1D meniscus) there is a critical slit width at which the meniscus length becomes infinite, meaning that the slit-like pore empties.
Solving the problem in 3D for an arbitrary capillary shape is much harder. Rascón and colleagues simplified the calculation by considering the energy needed to form a meniscus with a constant cross-sectional shape all along the tube: that is, one where the liquid “flattens out” and the tube empties. When this energy falls to zero, such a tube-emptying meniscus becomes stable. Using this method, the researchers could find the “emptying conditions” for a tube, which depend on parameters such as the contact angle of the bulk liquid with the wall (a measure of how strongly the wall attracts or repels the liquid), and the shape and width of the tube.
Surprise result
To the researchers’ surprise, they found that changing the liquid type and what the vessel is made of – which affects the contact angle – doesn’t have a big effect on whether a tube empties or not. Only for a narrow range of tube sizes does it matter at all; outside of this range, the tube will be filled or empty for any liquid.
The shape, on the other hand, matters a lot. For sufficiently flattened ellipse-shaped cross-sections, the tube will always empty, both for very small and very large contact angles, regardless of the tube width. In the former (hydrophilic) case, the strong liquid–wall interactions “pull” the liquid along the tube and out of the ends, while in the latter (hydrophobic) case, the very weak interactions mean that the liquid just “slips out”. This behaviour contradicts the conventional wisdom that very narrow horizontal capillaries will always hold onto their contents. “We could not believe what we were seeing in the maths,” says Parry.
“We all thought we understood how liquid can clog a very narrow tube, being incapable of flowing out no matter how we orient the capillary,” says Joseph Indekeu, a specialist on wetting at the Catholic University of Leuven in Belgium. But these results suggest that very narrow tubes may always empty for particular shapes of cross-section.
Capillaries with an equilateral triangular cross-section may also empty spontaneously, the researchers find, but the precise conditions for it depend on the orientation. Such behaviour has been discussed previously by applied-mathematician Robert Finn of Stanford University in California, US, who in 2011 showed that a tube with an “ice-cream-cone” cross-section – round at the top, sharply V-shaped at the bottom – will empty even in the absence of gravity, thanks to capillary forces alone. He and others have a patent on an “astronaut’s drinking cup” based on this principle. There is, says Finn, a “moderately substantive” body of work on the question of capillary emptying in the fluid-dynamics literature, partly to understand the question of how liquid “plugs” might block flow down narrow tubes.
Shape-based switches
The researchers say that such findings might be put to use in microfluidic technology. A change in shape of the tube (such as flattening of a circular cross-section) might induce flow – a kind of “pumping” – without requiring any change in fluid pressure. “I like very much the possibility of ‘lock and go’ switches, akin to traffic lights, for directing liquids in networks of capillaries, operated by simply rotating non-cylindrical tubes around their axes,” says Indekeu.
It’s possible too, says Parry, that examples of flow controlled by geometry might appear in nature, for example through changes in the shape of blood vessels or the v-like grooves of leaves and folded membranes.
The research is published in PNAS.