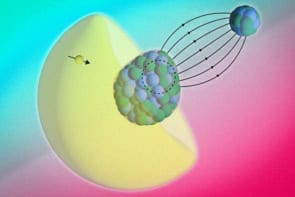
The quasiparticle concept allows physicists to describe complex, many-body interactions in terms of the behaviour of a single particle-like entity. Usually these particles turn up in condensed-matter systems such as semiconductors, but a new type of quasiparticle known as an angulon has been proposed to describe the rotation of an atomic or molecular impurity within a solvent. First proposed theoretically two years ago, angulons have now been shown to explain the curious behaviour of a range of different molecules rotating within liquid helium.
Physicists have been studying quasiparticles since at least the 1940s, when Lev Landau and Solomon Pekar put forward the idea of the polaron to describe the behaviour of an electron travelling through a crystal lattice. As the electron moves forward it disturbs the surrounding atoms and so polarizes that region of the crystal. Describing the process completely would involve calculating the changing interaction between the electron and vast numbers of atoms, but Landau realized that it could be approximated by regarding the electron and the associated polarizations as a single particle that acts like a more massive electron travelling through free space.
In the latest work, Mikhail Lemeshko of the Institute of Science and Technology Austria just outside Vienna has looked at the collective motion of a rotating molecule interacting with the many atoms inside a drop of superfluid helium. Such drops allow scientists to hold single molecules at a fraction of a degree above absolute zero and record their spectra without distortions. In particular, it is useful for studying very reactive molecules such as free radicals.
Not enough atoms
The system can be analysed semi-classically by assuming that the trapped molecule creates a shell of non-superfluid helium around itself as it rotates, so slowing it down. But superfluid helium is a fundamentally quantum-mechanical material that is described by Bose–Einstein, as opposed to classical Boltzmann, statistics. Physicists have carried out brute-force numerical simulations of the system in recent years, but the complexity of the many-body interactions has limited the number of helium atoms in those simulations to around 100. The droplets used in experiments, in contrast, tend to contain more than 1000 atoms.
Lemeshko has found that he can simplify the problem enormously by using the concept of the angulon. Just as a polaron consists of an electron plus the deformations in the surrounding lattice, so an angulon is made up of the rotating molecule plus the disturbances it creates in the surrounding helium. And whereas a polaron is in effect a free-moving but more massive version of the electron, an angulon acts like an un-trapped version of the molecule in question but with a larger moment of inertia.
Having put forward the theory of angulons with Richard Schmidt of the Harvard-Smithsonian Center for Astrophysics in the US in 2015, Lemeshko has now compared that theory against 20 years of experimental results. For each of 25 different molecules, Lemeshko calculates the effect of the surrounding helium atoms on the molecule’s rotational constant – which is inversely proportional to its moment of inertia – and then compares the modified constant to the value obtained experimentally.
Two regimes
This was not a straightforward one-size-fits-all comparison, however. To obtain simple analytic expressions for molecular rotation, Lemeshko solved the angulon problem in two “regimes”. One regime, mainly applicable to heavy molecules such as those containing atoms of sulphur, involves molecules with significant coupling to the helium (a high potential energy) but with little kinetic energy. Conversely, the other regime, relevant to lighter molecules such as water, entails greater amounts of kinetic energy but weak coupling.
Although not all the predictions within the strong-coupling regime ended up within the experimental uncertainty, Lemeshko considers that for most heavy molecules he achieved “a good agreement with experiment”. He did even better in the weak-coupling regime, getting to within 2% of the experimental values for most light molecules. With some of the medium-sized molecules, however, he struggled, being unable to accurately predict their modified rotational constants within either the strong- or weak-coupling regimes. He says that an “intermediate-coupling” theory for angulons could in principle make accurate predictions here, but adds that rough estimates can be achieved in the meantime by splitting the difference between the strong- and weak-coupling predictions.
Despite the problems, Lemeshko concludes that the results of his study “provide strong evidence” that molecules rotating within superfluid helium do indeed form angulons. “An angulon is not a real physical entity in the sense that a fundamental particle such as an electron is,” he says. “But it is as real as any other quasiparticle.”
Electron angulons
Lemeshko is now looking to apply his theory beyond molecules within liquid helium. For example, he is investigating whether angulons could be used to represent electrons exchanging their orbital angular momentum with a crystal lattice. Doing so, he says, might aid the development of ultrafast switching and advanced data storage, but he cautions that this research is “very preliminary”.
The research is described in Physical Review Letters.