Work can be extracted from a single heat bath at the boundary between classical and quantum thermodynamics
Modern society relies heavily on the conversion of heat into mechanical work. The first heat engines were responsible for the industrial revolution, but behind the scenes they were also fuelling the development of thermodynamics. In 1824 Sadi Carnot’s interest in improving the performance of steam engines led him to think about the efficiency of a heat engine in a new and fundamental way. He concluded that the maximum efficiency of a heat engine that absorbs heat from a reservoir at a given temperature, T2, and rejects heat to another reservoir at a lower temperature, T1, is η = 1 – T1/T2. In other words it is impossible to extract work from a single heat bath – a rule that we now know to be a consequence of the second law of thermodynamics.
Then came quantum mechanics. Classical thermodynamics tends to work for large numbers of atoms or molecules, which means that some quantum systems can at first appear to violate its basic laws. Now Marlan Scully and co-workers at Texas A&M University and Herbert Walther at the Max-Planck Institute for Quantum Optics in Garching have proposed a “quantum Carnot engine” that displays features that are simply not possible with a classical engine. In particular, their quantum engine can extract work from a single heat bath (M O Scully et al. 2003 Science 299 862-864).
Quantum steam
Carnot’s conceptual heat engine operated in cycles such that there is no change in the internal energy of the working fluid – such as steam – during a cycle. More heat is converted to work as the number of operating cycles increases, without the engine itself being a source of any work. In particular he considered a reversible closed cycle consisting of two isothermal (constant temperature) processes and two adiabatic (no external exchange of heat) processes. He showed that no heat engine operating between two temperatures could be more efficient than a Carnot cycle. But he was wrong.
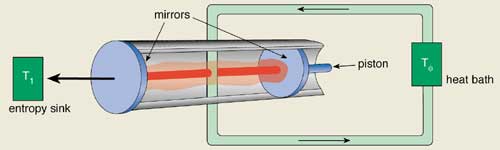
The “steam” in the new quantum Carnot engine considered by Scully and colleagues comes in the form of photons. The radiation pressure from the photons drives a piston in an optical cavity, which also doubles as one of the cavity mirrors. The other cavity mirror is used to exchange heat with a heat sink at temperature T1. A second heat bath at a higher temperature T2 is required as a source of heat for the radiation, in analogy with the classical Carnot engine.
Scully and co-workers take this source of heat to be a stream of hot atoms, which flows through the cavity and exchanges energy with the photons through emission and absorption processes. These atoms flow out of the cavity at a cooler temperature and are then reheated in a second cavity known as a “hohlraum”. Once the atoms have been heated to T2 they are re-injected into the first cavity for the next cycle of the quantum Carnot engine (see figure).
The quantum and classical Carnot engines therefore operate in the same way – a closed cycle of two isothermal and two adiabatic processes. However, in its simplest form the quantum Carnot engine cannot extract work from a single heat bath. If Qin is the energy absorbed from the bath atoms during the isothermal expansion and Qout is the energy given to the heat sink during the isothermal compression, then the efficiency of the engine is η = (Qin – Qout)/Qin. If the bath atoms are assumed to be two-state systems that absorb and emit radiation at the same frequency, then standard thermodynamic formulas for the photon gas reveal that the efficiency of the quantum Carnot engine is η = 1 – T1/T2 – just as it is for the classical Carnot engine.
Quantum coherence
The new twist in the quantum engine occurs when the bath atoms have three states instead of two, which can result in what is called quantum coherence. If there is a non-vanishing phase difference between the two lowest atomic states, then the atoms are said to have quantum coherence. This can be induced by a microwave field with a frequency that corresponds to the transition between the two lowest atomic states.
Quantum coherence changes the way the atoms interact with the cavity radiation by changing the relative strengths of emission and absorption. The idea is that the atoms leaving the hohlraum at temperature T2 pass through a microwave cavity that causes them to become coherent with phase φ before they enter the optical cavity. They still cause the cavity radiation to come into thermal equilibrium, but the temperature that characterizes the radiation is now Tφ = T2(1 – nεcosφ), where n is the average number of photons for a thermal field at temperature T2, and ε is a small number that characterizes the magnitude of the quantum coherence.
The efficiency of the quantum-coherent Carnot engine can then be expressed as ηφ = (Tφ – T1)/T1. If ε is small, this becomes ηφ ~ η – (T1/T2)nεcosφ, where η is the efficiency of a classical Carnot engine as before. Thus, depending on the value of φ, the efficiency of the quantum Carnot engine can exceed that of the classical engine – even when T1 = T2. It can therefore extract work from a single heat bath.
And the second law?
At first glance this might seem trivial, since the atoms leaving the hohlraum are simply made hotter by the microwave generator, causing the radiation field to become hotter than the temperature of the hohlraum. This is not the case. Microwave heating of the atoms has no direct effect on the temperature Tφ of the cavity radiation. It is the quantum coherence that is induced by the microwave that makes Tφ different from the hohlraum temperature. There is, of course, a cost for this coherence – the microwave energy required to produce the coherence must exceed the net energy that is extracted from the heat bath.
Furthermore, extracting work from a quantum Carnot engine does not violate the second law of thermodynamics because the quantum coherence also costs extra entropy, which ensures that the overall entropy of the system is always increasing.
Practicalities aside, a quantum Carnot engine may one day provide a “quantum afterburner” that will increase the efficiency of a conventional combustion engine. Such a hybrid device would exploit the temperature difference between the combustion and exhaust phases of the four-stroke Otto cycle (see “The energy-saving quantum afterburner” Physics World March 2002 p6 print version only).
The point is that atoms with quantum coherence constitute a substance that is fundamentally different from conventional working fluids such as steam or Freon, which allows us to extend our understanding of thermodynamics at the interface of classical and quantum physics.



