
Imagine a parallel universe where physicists are remunerated so handsomely that they can accumulate multitudinous assets. In this alternate universe, you naturally wish to share your good fortune, so you decide to divide your assets equally between your two non-physicist friends. This is an example of the number partitioning problem, in which the aim is to partition a single list of integers into two balanced lists in a way that minimizes the discrepancy between the sums of each list. In this example, the integers correspond to the values of your assets and the balanced lists represent the assets going to each friend.
Your enthusiasm wanes, however, when you find out that this seemingly simple task is notoriously hard. In fact, the number partitioning problem is classed as NP-hard, meaning that an optimal solution is difficult to find but easy to verify.
Researchers at Stanford University have now developed a quantum approach. By applying a well-established quantum algorithm known as Grover’s algorithm to the number partitioning problem, they obtain a quadratic speedup compared to equivalent classical algorithms. The team also proposes a way to implement this algorithm in near-term quantum devices such as those using cold atoms.
General approach
Grover’s algorithm is designed to find a specific item in a database, and it relies on a so-called oracle to judge whether a given item is the target of the search. Once each item in the database is encoded as a distinct quantum state, the next step is to construct an equally weighted superposition of these states. After that, the oracle is applied to the superposition so that it imparts a phase difference on the quantum state that encodes the target item. This marks the target, after which its probability of being measured can be boosted. The process is then applied repeatedly until the measurement probability is sufficiently high.
The Stanford researchers apply Grover’s algorithm to the number partitioning problem by encoding each possible partition of the integer list as a quantum state. They also formulate an oracle that can identify an optimal partition, which is possible because solutions of NP-hard problems are easy to verify. Grover’s algorithm then searches for an optimal partition.
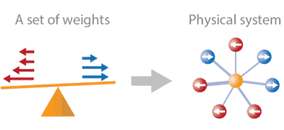
To implement the algorithm, the physicists propose a hardware architecture in which a central quantum spin (such as a Rydberg atom) or a central boson (such as a bosonic mode from a cavity) is coupled to all the other spins in the system, with no other couplings present. This arrangement is known as a star graph (see image). The central entity acts as the oracle, and its coupling strengths to the other spins represent the integers in the list.
Future directions
“Our proposal opens the possibility of implementing Grover’s algorithm efficiently on devices before full quantum error correction is achieved, improving the prospects of tackling real-world problems on these near-term devices,” says Ognjen Marković, a co-author of the study.

Microwaves in metamaterial perform quantum search
Marković also believes that this work could stimulate research in the field of quantum-classical hybrid algorithms. For instance, the team’s proposed implementation of Grover’s algorithm could be used as a quantum subroutine in a larger, possibly classical algorithm.
The research is reported in PRX Quantum.



