Is there a secret that makes a Stradivarius sound so good, and can modern violins match the wonderful tonal quality of this great Italian instrument, asks Colin Gough.
Colin Gough received the 2001 Science Writing Award for Professionals in Acoustics from the Acoustical Society of America for this article.

Is there really a lost secret that sets Stradivarius violins apart from the best instruments made today? After more than a hundred years of vigorous debate, this question remains highly contentious, provoking strongly held but divergent views among players, violin makers and scientists alike. All of the greatest violinists of modern times certainly believe it to be true, and invariably perform on violins by Stradivari or Guarneri in preference to modern instruments.
Violins by the great Italian makers are, of course, beautiful works of art in their own right, and are coveted by collectors as well as players. Particularly outstanding violins have reputedly changed hands for over a million pounds. In contrast, fine modern instruments typically cost about £10 000, while factory-made violins for beginners can be bought for under £100. Do such prices really reflect such large differences in quality?
The violin is the most highly developed and most sophisticated of all stringed instruments. It emerged in Northern Italy in about 1550, in a form that has remained essentially unchanged ever since. The famous Cremonese violin-making families of Amati, Stradivari and Guarneri formed a continuous line of succession that flourished from about 1600 to 1750, with skills being handed down from father to son and from master to apprentice. The popular belief is that their unsurpassed skills, together with the magical Stradivarius secret, were lost by the start of the 19th century.
Every violin, whether a Stradivarius or the cheapest factory-made copy, has a distinctive “voice” of its own. Just as any musician can immediately recognize the difference between Domingo and Pavarotti singing the same operatic aria, so a skilled violinist can distinguish between different qualities in the sound produced by individual Stradivari or Guarneri violins. The challenge for scientists is to characterize such differences by physical measurements. Indeed, over the last century and a half, many famous physicists have been intrigued by the workings of the violin, with Helmholtz, Savart and Raman all making vital contributions.
It is important to recognize that the sound of the great Italian instruments we hear today is very different from the sound they would have made in Stradivari’s time. Almost all Cremonese instruments underwent extensive restoration and “improvement” in the 19th century. You need only listen to “authentic” baroque groups, in which most top performers play on fine Italian instruments restored to their former state, to recognize the vast difference in tone quality between these restored originals and “modern” versions of the Cremonese violins.
Prominent among the 19th-century violin restorers was the French maker Vuillaume, whose copy of a Guarnerius violin is shown above left. Vuillaume worked closely with Felix Savart, best known to physicists for the Biot-Savart law in electromagnetism, to enhance the tone of early instruments. Vuillaume, Savart and others wanted to produce more powerful and brilliant sounding instruments that could stand out in the larger orchestras and concert halls of the day. Improvements in instrument design were also introduced to support the technical demands of great violin virtuosi like Paganini.
Back to basics: the components of a violin
To understand the factors that determine the quality of sound produced by particular instruments, we must first recall how the violin works (figure 1). Sound is produced by drawing a bow across one or more of the four stretched strings. The string tensions are adjusted by tuning pegs at one end of the string, so that their fundamental frequencies are about 200, 300, 440 and 660 Hz – which correspond to the notes G, D, A and E. However, the strings themselves produce almost no sound.
To produce sound, energy from the vibrating string is transferred to the main body of the instrument – the so-called sound box. The main plates of the violin act rather like a loudspeaker cone, and it is the vibrations of these plates that produce most of the sound.
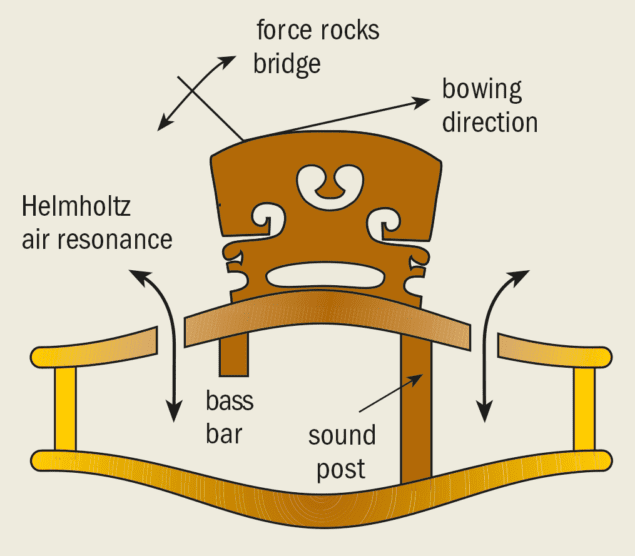
The strings are supported by the “bridge”, which defines the effective vibrating length of the string, and also acts as a mechanical transformer. The bridge converts the transverse forces of the strings into the vibrational modes of the sound box. And because the bridge has its own resonant modes, it plays a key role in the overall tone of the instrument.
The front plate of the violin is carved from a solid block of fine-grained pine. Maple is usually used for the back plate and pine for the sides. Two expertly carved and elegantly shaped “f-holes” are also cut into the front plate. The carving of the f-holes often helps to identify the maker of a valuable instrument: never rely on the label inside the violin to spot a fake instrument as the label will probably have been forged as well.
The f-holes play a number of important acoustic roles. By breaking up the area of the front plate, they affect its vibrational modes at the highest frequencies. More importantly, they boost the sound output at low frequencies. This occurs through the “Helmholtz air resonance”, in which air bounces backwards and forwards through the f-holes. The resonant frequency is determined by the area of the f-holes and the volume of the instrument. It is the only acoustic resonance of the instrument over which violin makers have almost complete control.
Early in the 16th century it was discovered that the output of stringed instruments could be increased by wedging a solid rod – the “sound post” – between the back and front plates, close to the feet of the bridge. The force exerted by the bowed strings causes the bridge to rock about this position, causing the other side of the plate to vibrate with a larger amplitude. This increases the radiating volume of the violin and produces a much stronger sound.
The violin also has a “bass bar” glued underneath the top plate, which stops energy being dissipated into acoustically inefficient higher-order modes. The bass bar and sound post were both made bigger in the 19th century to strengthen the instrument and to increase the sound output.
Getting kinky: how strings vibrate
In the 19th century the German physicist Hermann von Helmholtz showed that when a violin string is bowed, it vibrates in a way that is completely different from the sinusoidal standing waves that are familiar to all physicists. Although the string vibrates back and forth parallel to the bowing direction, Helmholtz showed that other transverse vibrations of the string could also be excited, made up of straight-line sections. These are separated by “kinks” that travel back and forth along the string and are reflected at the ends. The kinks move with the normal transverse-wave velocity, c = (T/m)1/2, where T is the tension and m the mass per unit length of the string. The bowing action excites a Helmholtz mode with a single kink separating two straight sections (figure 2).
When the kink is between the bow and the fingered end of the string, the string moves at the same speed and in the same direction as the bow. Only a small force is needed to lock the two motions together. This is known as the “sticking regime” (figure 2a). But as soon as the kink moves past the bow – on its way to the bridge and back – the string slips past the bow and starts moving in the opposite direction to it. This is known as the “slipping regime” (figure 2b).
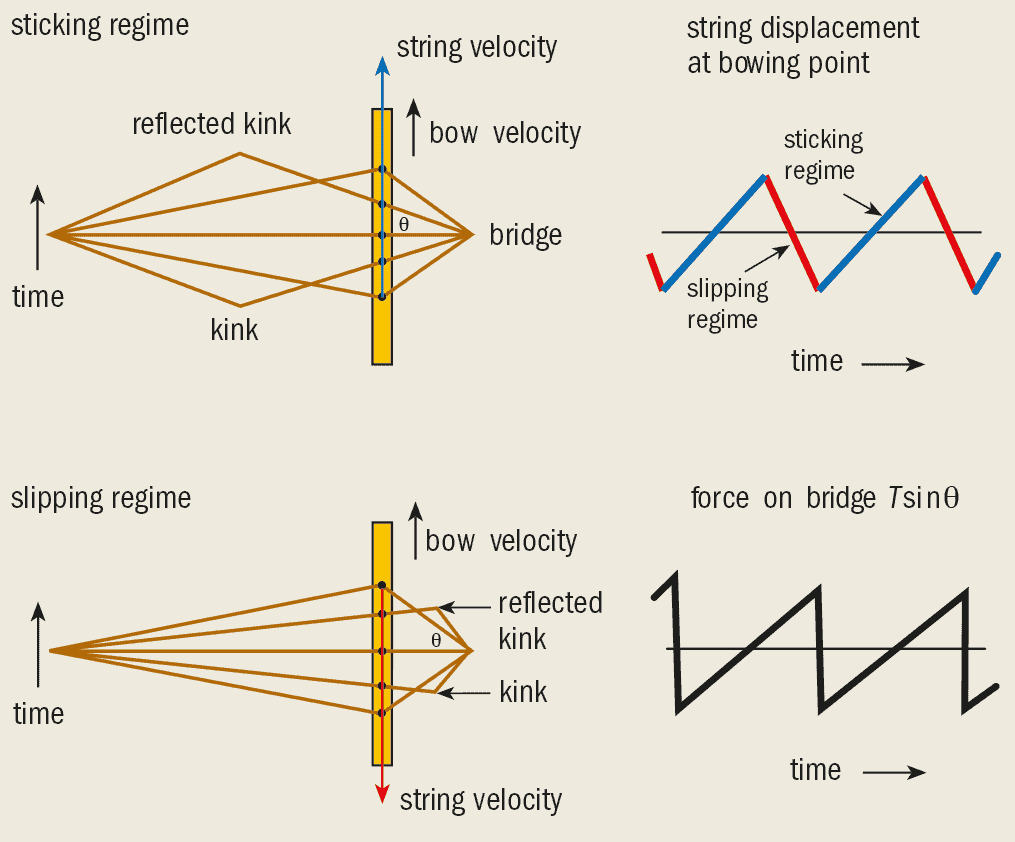
Although the sliding friction is relatively small in the slipping regime, energy is continuously transferred from the strings to the vibrational modes of the instrument at the bridge. Each time the kink reflects back from the bridge and passes underneath the bow, the bow has to replace the lost energy. It therefore exerts a short impulse on the string so that it moves again at the same velocity as the bow.
This process is known as the “slip-stick” mechanism of string excitation and relies on the fact that sliding friction is much smaller than sticking friction (figure 2c). The Helmholtz wave generates a transverse force Tsinq on the bridge, where q is the angle of the string at the bridge. This force increases linearly with time, but its amplitude reverses suddenly each time the kink is reflected at the bridge, producing a sawtooth waveform (figure 2d). The detailed physics of the way a bow excites a string has been extensively studied by Michael McIntyre and Jim Woodhouse at Cambridge University, who have made a number of important theoretical and experimental contributions to violin acoustics in recent years.
It is important to recognize that the Helmholtz wave is a free mode of vibration of the string. The player has to apply just the right amount of pressure to excite and maintain the waveform without destroying it. The lack of such skill is one of the main reasons why the sound produced by a beginner is so excruciating. Conversely, the intensity, quality and subtlety of sound produced by great violinists is mainly due to the fact that they can control the Helmholtz waveform with the bow. The quality of sound produced by any violin therefore depends as much on the bowing skill of the violinist as on the physical properties. One of the reasons that the great Cremonese violins sound so wonderful is because we hear them played by the world’s greatest players!
Sounds good: how a violin makes a noise
The sawtooth force that is generated on the top of the bridge by a bowed string is the input signal that forces the violin to vibrate and radiate sound – rather like the electrical input to a loudspeaker, albeit with a much more complicated frequency response. The input sawtooth waveform has a rich harmonic content, consisting of numerous Fourier components.
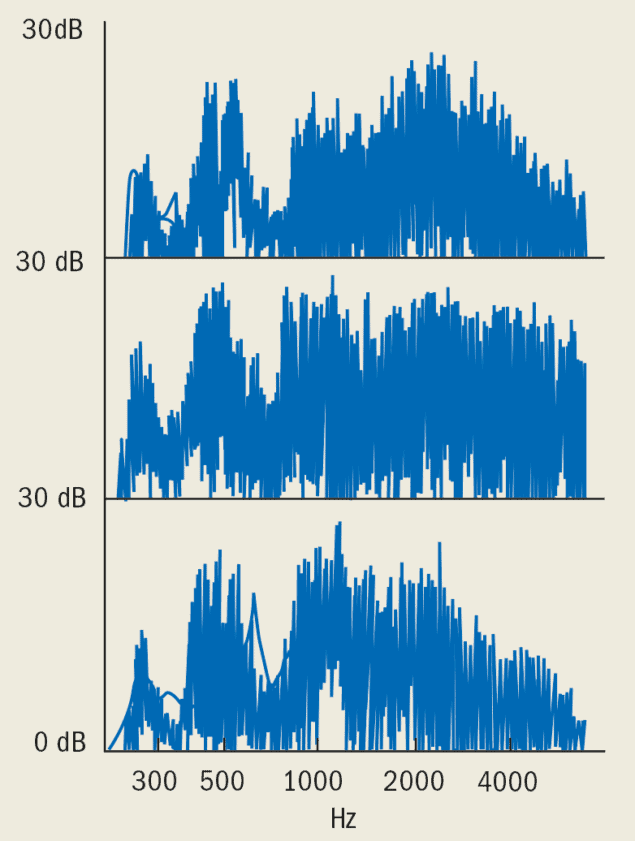
Since the violin is a linear system, the same Fourier components or “partials” appear in the output of the violin. The amplitude of each partial in the radiated sound is determined by the response of the instrument at that particular frequency. This is largely determined by the mechanical resonances of the bridge and by the body of the instrument. These resonances are illustrated schematically in figure 3, where typical responses have been mathematically modelled to simulate their influence on the sound produced.
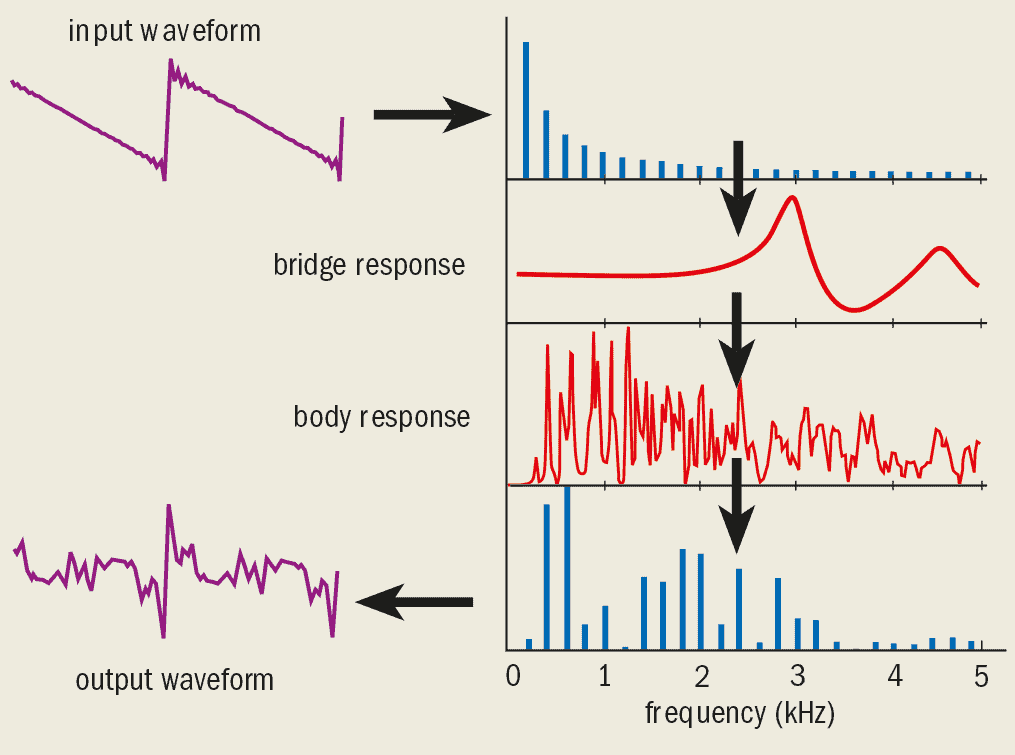
At low frequencies the bridge simply acts as a mechanical lever, since the response is independent of frequency. However, between 2.5 and 3 kHz the bowing action excites a strong resonance of the bridge, with the top rocking about its narrowed waist section. This boosts the intensity of any partials in this frequency range, where the ear is most sensitive, and gives greater brightness and carrying power to the sound. Another resonance occurs at about 4.5 kHz in which the bridge bounces up and down on its two feet. Between these two resonances there is a strong dip in the transfer of force to the body. Thankfully this dip decreases the amplitude of the partials at these frequencies, which the ear associates with an unpleasant shrillness in musical quality.
The sinusoidal force exerted by the bridge on the top plate produces an acoustic output that can be modelled mathematically. The output increases dramatically whenever the exciting frequency coincides with one of the many vibrational modes of the instrument. Indeed, the violin is rather like a loudspeaker with a highly non-uniform frequency response that peaks every time a resonance is excited. The modelled response is very similar to many recorded examples made on real instruments.
In practice, quite small changes in the arching, thickness and mass of the individual plates can result in big changes in the resonant frequencies of the violin, which is why no two instruments ever sound exactly alike. The multi-resonant response leads to dramatic variations in the amplitudes of individual partials for any note played on the violin.
Such factors must have unconsciously guided the radical redesign of the bridge in the 19th century. Violinists often place an additional mass (the “mute”) on the top of the bridge, effectively lowering the frequency of the bridge resonances. This results in a much quieter and “warmer” sound that players often use as a special effect. It is therefore surprising that so few players – or even violin makers – recognize the major importance of the bridge in determining the overall tone quality of an instrument.
One of the reasons for the excellent tone of the very best violins is the attention that top players give to the violin set-up – rather like the way in which a car engine is tuned to get the best performance. Violinists will, for example, carefully adjust the bridge to suit a particular instrument – or even select a different bridge altogether. The sound quality of many modern violins could undoubtedly be improved by taking just as much care in selecting and adjusting the bridge.
The transfer of energy from the vibrating string to the acoustically radiating structural modes is clearly essential for the instrument to produce any sound. However, this coupling must not be too strong, otherwise the instrument becomes difficult to play and the violinist has to work hard to maintain the Helmholtz wave. Indeed, a complete breakdown can occur when a string resonance coincides with a particularly strongly coupled and lightly damped structural resonance.
When this happens the sound suddenly changes from a smooth tone to a quasi-periodic, uncontrollable, grunting sound – the “wolf-note”. Players minimize this problem by wedging a duster against the top plate to dampen the vibrational modes, or by placing a resonating mass, the “wolf-note adjuster”, on one of the strings on the far side of the bridge. However, this only moves the wolf-note to a note that is not played as often, rather than eliminating it entirely.
The Helmholtz motion of the string and the wolf-note problem were extensively studied by the Indian physicist Chandrasekhara Raman in the early years of the 20th century. His results were published in a series of elegant theoretical and experimental papers soon after he founded the Indian Academy of Sciences and before the work on optics that earned him the Nobel Prize for Physics in 1930.
Good vibrations: the role of resonances
The existence of so many resonances at almost random frequencies means that there is simply is no such thing as a “typical” waveform or spectrum for the sound from a violin. Indeed, there is just as much variation between the individual notes on a single instrument as there is between the same note played on different instruments. This implies that the perceived tone of a violin must be related to overall design of the instrument, rather than to the frequencies of particular resonances on an instrument.
An interesting attempt to look for such global properties was recently made by the violin maker Heinrich Dünnwald in Germany. He measured the acoustic output of 10 Italian violins, 10 fine modern copies and 10 factory-made violins, all of which were excited by an electromagnetic driver on one side of the bridge (figure 4). Between 400 and 600 Hz, the factory-made violins were found – surprisingly – to be closer to the Italian instruments than the modern copies. At frequencies above 1000 Hz, however, the factory-made instruments had a rather weak response – in contrast to the over-strong response of the modern violins, which may contribute to a certain shrillness in their quality.
In practice it is extremely difficult to distinguish between a particularly fine Stradivarius instrument and an indifferent modern copy on the basis of the measured response alone. The ear is a supreme detection device and the brain is a far more sophisticated analyser of complex sounds than any system yet developed to assess musical quality.
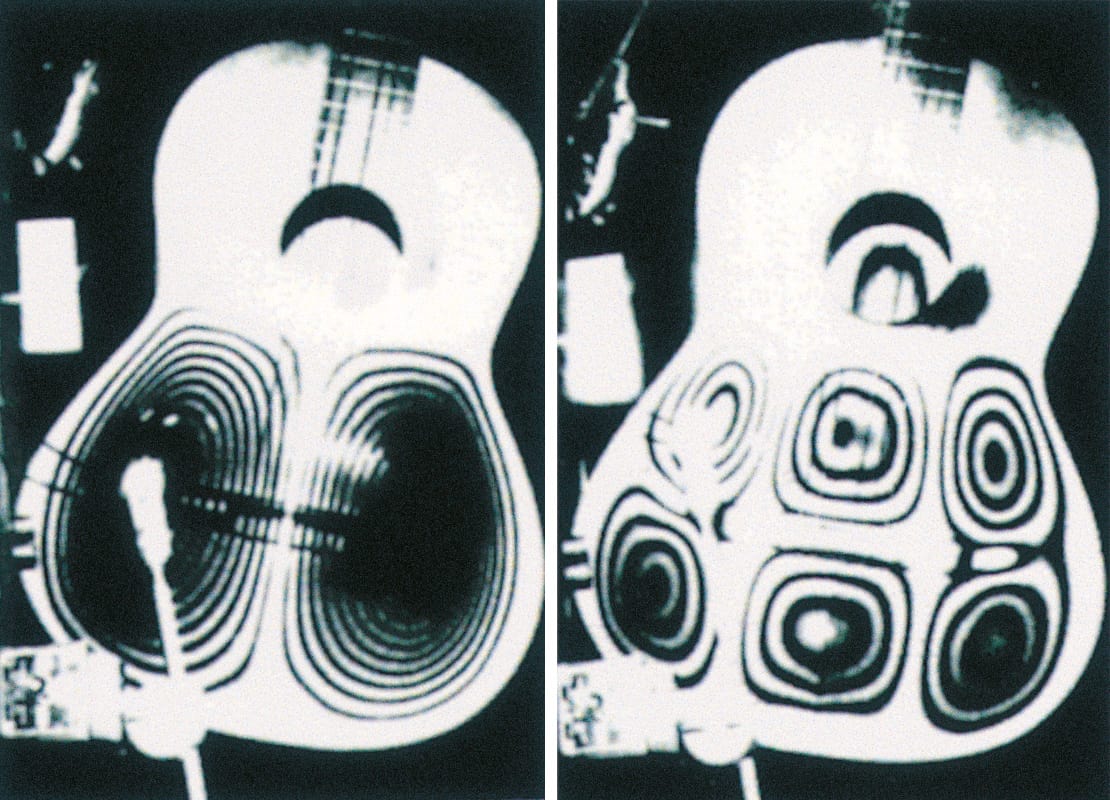
Although such measurements give the frequencies of important acoustic resonances, they tell us nothing about the way a violin actually vibrates. A powerful technique for investigating such vibrations is called time-averaged interference holography. Bernard Richardson, a physicist at Cardiff University in the UK, has made a number of such studies on the guitar and violin. Some particularly beautiful examples for the guitar are shown in figure 5. Unfortunately, it is not easy to obtain similar high-quality images for the violin because it is smaller, the vibrations of the surface are smaller, and the surfaces of the violin are more curved and less reflective than those of the guitar.
Another powerful approach is modal analysis: a violin is lightly struck with a calibrated hammer at several positions and the transient response at various points is measured with a very light accelerometer. These responses are then analysed by computer to give the resonant frequencies and structural modes of vibration of the whole instrument. This technique has been used to teach students about violin acoustics at the famous Mittenwald school of violin making in Germany and by Ken Marshall in the US. Marshall has also shown that the way the violin is held has little effect on its resonant response.
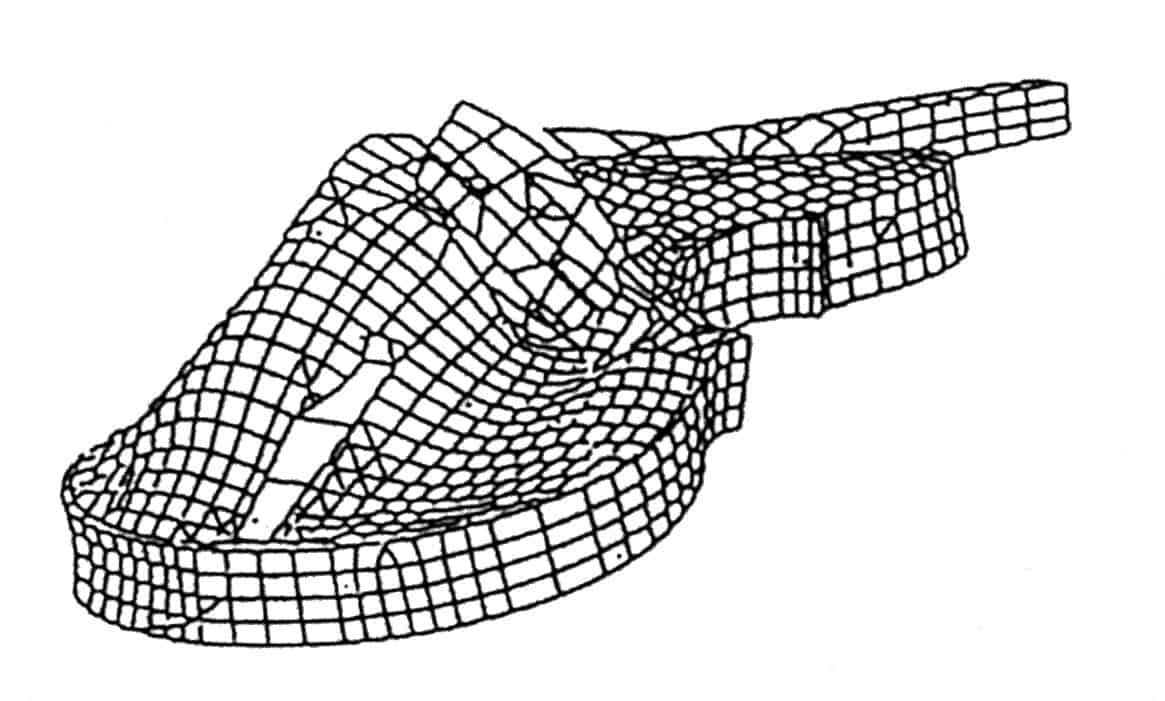
Similar information can be obtained by finite-element analysis: the violin is modelled as a set of masses that are connected by springs, which makes it relatively straightforward to evaluate the resonant modes and associated vibrations of the whole structure (figure 6). Various physical parameters of the materials used to make the violin can also be incorporated in the calculations. It is then possible to construct a virtual violin and to predict all its vibrational and acoustic properties. This might be the first step towards designing a violin with a specified response and hence tonal quality – once we know how to define “quality” in a measurable way.
Build quality: how to make a good violin
So how do skilled violin makers optimize the tone of an instrument during the construction process? They begin by selecting a wood of the highest possible quality for the front and back plates, which they test by tapping with a hammer and judging how well it “rings”.
The next important step is to skilfully carve the plates out of the solid wood, taking great care to get the right degree of arching and variations in thickness. The craftsman has to learn how to adjust the plates to produce a fine-sounding instrument. Traditional makers optimize the thickness by testing the “feel” of the plates when they are flexed, and by the sounds produced when the are tapped at different positions with the knuckles. This is the traditional equivalent of nodal analysis, with the violin maker’s brain providing the interpretative computing power.
However, in the last 50 years or so, a group of violin makers has emerged who have tried to take a more overtly scientific approach to violin making. The pioneer in this field was Carleen Hutchins, the doyenne of violin acoustics in the US. Now almost 90 years old, but still active in the field, she founded the Catgut Society of America in 1958, together with William Saunders of “Russell-Saunders coupling” fame and John Schelling, a former director of radio research at Bell Labs. The society brings together violin makers and scientists from across the world, with the common aim of advancing our understanding of violin acoustics and developing scientific methods to help makers improve the quality of their instruments.
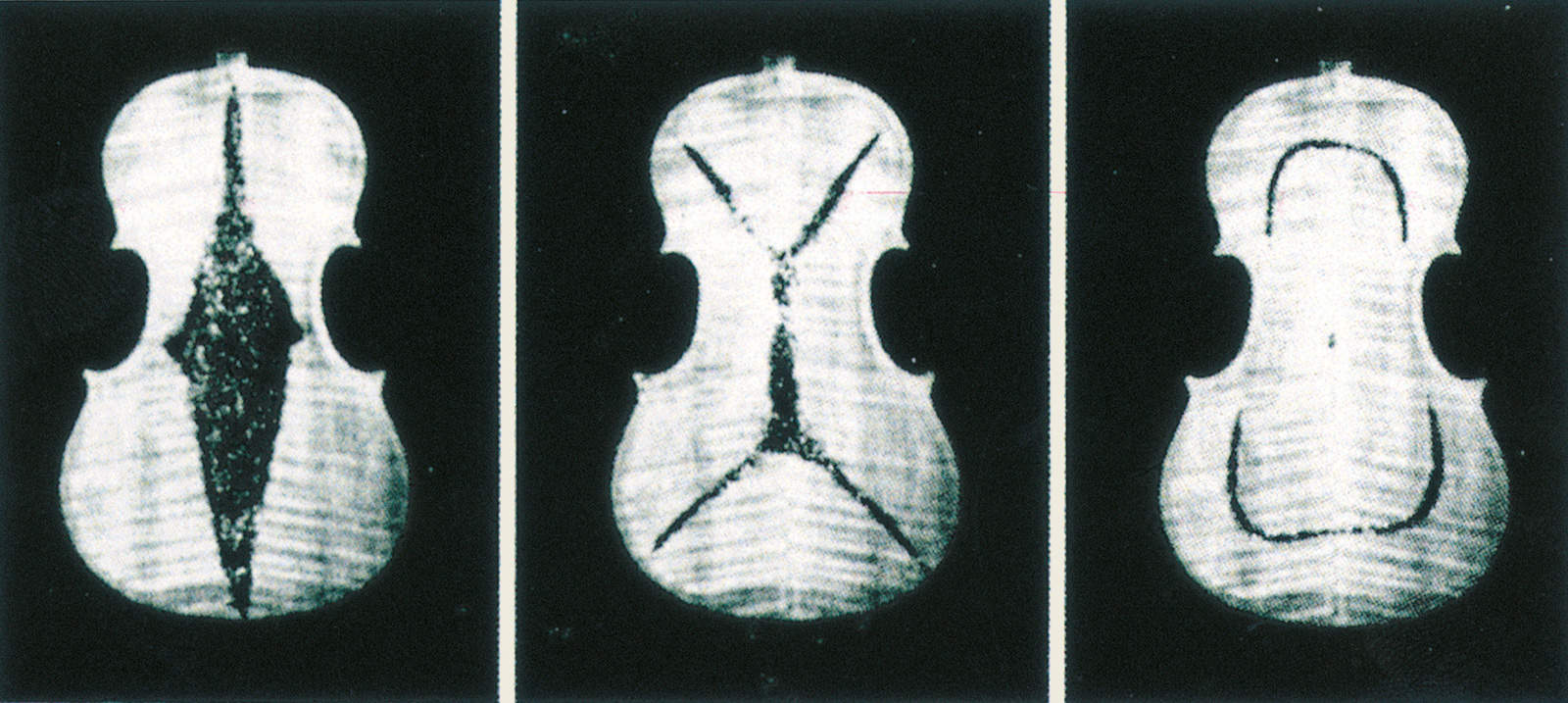
One common practice that has been adopted by violin makers has been to replace the traditional flexing and tapping of plates by controlled measurements. During the carving process, the thinned plates are suspended horizontally above a large loudspeaker. The acoustic resonances excited by the loudspeaker can readily be identified by sprinkling glitter onto the surface of the plates. When the loudspeaker has excited a resonance, the glitter bounces up and down, and moves towards the nodal lines of the resonant modes excited (figure 7). The aim is to interactively thin or “tune” the first few free-plate resonances to specified frequencies and nodal patterns.
Unfortunately, there are very few examples of such measurements for really fine Italian instruments because their owners are naturally reluctant to allow their violins to be taken apart for the sake of science. The relatively few tests that have been performed suggest that the early Italian makers may have tuned the resonant modes of the individual plates – which they could identify as they tapped them – to exact musical intervals. This would be consistent with the prevailing Renaissance view of “perfection”, which was measured in terms of numbers and exact ratios.
Members of the “scientific” school of violin makers might reasonably claim that this could be the lost Stradivarius secret. However, it must indeed have been secret, since there is no historical evidence to support the case. Although many first-class modern violins have been built based on these principles, there is little evidence to suggest that they are any better than many fine instruments made with more traditional methods.
However, neither traditional craftsmanship nor scientific methods can hope to control the detailed resonant structure of an instrument in the acoustically important range above 1 kHz. Even the tiniest changes in the thickness of the plates will significantly affect the specific resonances in this frequency range, as will the inevitable variations in the properties of the wood. Furthermore, the frequencies and distribution of the resonant modes of the violin depend on the exact position of the sound post, which imposes an additional constraint on the modes that can be excited. Top players regularly return their instruments to violin makers, who move the sound post and adjust the bridge in an effort to optimize the sound. This means that there is no unique set of vibrational characteristics for any particular instrument – not even a Stradivarius!
Knotty problem: the effects of wood
Another factor that affects the quality of a violin is the internal damping of the wood. This strongly affects the multi-resonant response of the instrument and the overall background at high frequencies. In particular, the difference between the peaks and troughs of the resonant response is determined by the quality-factor of the resonances. This largely depends on internal losses within the wood when it vibrates: only a small fraction of the energy is lost by acoustic radiation.
The strongly peaked frequency response of the violin has a dramatic influence on the sound produced when “vibrato” is used. In this playing technique, the finger stopping the string is cyclically rocked backwards and forwards, periodically changing the pitch of the note. Because the response has such strong peaks and troughs, any change in pitch also produces cyclic variations in the overall amplitude, waveform and spectral content of the sound (figure 8).
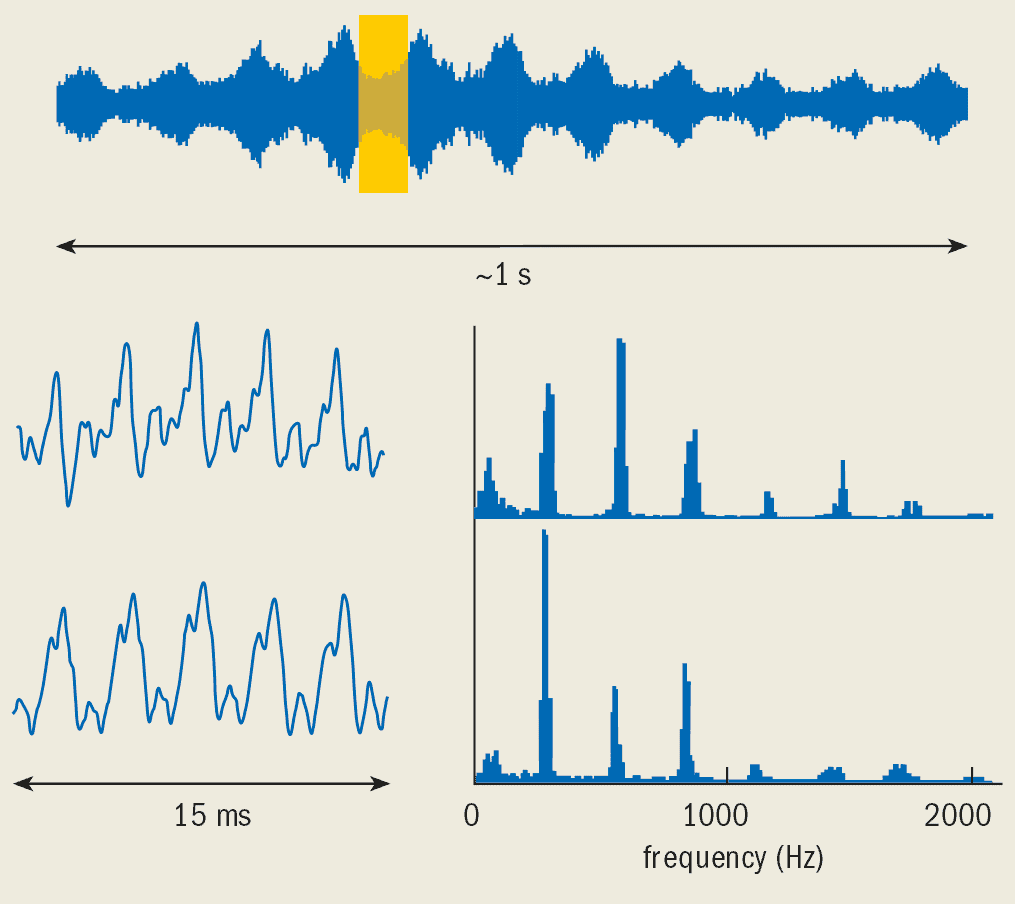
Vibrato is very common nowadays because it captures and holds the attention of the listener, enabling the solo violin to be heard even when accompanied by a large orchestra. It would have been considered far less important when Stradivari was alive because vibrato was used only for special theatrical effects and the violin was expected to blend in with other instruments.
Vibrato adds a certain “lustre” and interest to the quality of sound produced because the ear is particularly sensitive to changes in the waveform. In a recent radio broadcast, for example, the English violinist Tasmin Little demonstrated the marvellous tone of the Stradivarius violin used by Nathan Milstein, one of the finest violinists of recent times. After playing just a few notes on the violin, she described the tone as “wonderfully exciting, almost deafening, very vibrant. It is alive. It has an incredible ring under my ear. It is amazing”. There can be little doubt that Little’s subjective assessment is directly related to the extremely large changes in amplitude, waveform and spectral content associated with the use of vibrato, which gives “life and vibrancy” to the sound.
To achieve such large changes in the frequency response of the violin, the individual resonances of the instrument have to be strongly peaked, which requires high-quality wood with low internal damping. Unfortunately, wood can absorb water, which increases the damping: this explains why violinists often notice that the responsiveness of an instrument, which includes the ability to control the sound quality using vibrato, changes with temperature and humidity.
The choice of high-quality wood for making instruments has always been recognized by violin makers, and well seasoned wood is generally recommended. However, by measuring the pattern of growth-rings in the wood of a Stradivarius, we know that the Italian violin makers sometimes used planks of wood that had only been seasoned for five years. However, such wood is now 300 years old, and the intrinsic internal damping will almost certainly have decreased with time, as the internal organic structure has dried out.
The same will obviously be true for all old Italian instruments. The age of the wood may therefore automatically contribute to the improved quality of the older instruments. This may also explain why the quality of a modern instrument appears to change in its first few years. Surprisingly, many players still believe that their instruments improve because they are loved and played well, which would be very difficult to explain on any rational scientific basis!
The secret at last?
Many other theories have been put forward to account for the Stradivarius secret. The most popular for well over a century has been that the varnish had some sort of “magic” composition. The main function of the varnish is to protect the instrument from dirt and to stop it absorbing moisture from the player’s hands. The varnish also imparts great aesthetic value to the instrument, with its translucent coating highlighting the beautiful grain structure of the wood below.
However, historical research has shown that the varnish is no different to that used by many furniture makers when Stradivari was alive. Claire Barlow and co-workers at Cambridge University, for example, have used electron microscopy to identify many of the important ingredients of the varnish itself, and the materials that are used to smooth the surface before the varnish is applied. It turns out that most could easily have been bought from the pharmacist shop next to Stradivari’s workshop. Apart from the possibility that the varnish was contaminated with the wings of passing insects and debris from the workshop floor, there is no convincing evidence to support the idea of a secret formula!
Indeed, ultraviolet photography has revealed that many fine-sounding Italian violins have lost almost all their original varnish, and were recoated during the 19th century or later. The composition of the varnish is therefore unlikely to be the long-lost secret, although too much varnish would certainly increase the damping and therefore sully the tone.
Other researchers, meanwhile, have claimed that Stradivari’s secret was to soak the wood in water, to leach out supposedly harmful chemicals, before it was seasoned. Although this would be consistent with the idea that the masts and oars of recently sunken Venetian war galleys might have been used to make violins, the scientific and historical evidence to support this view is unconvincing.

The sound of trust
Over the last 150 years, physicists have made considerable progress in understanding the way the violin works. In the 19th century the “modernized” Stradivarius violin emerged with an “enhanced” tone as a result of scientifically guided “improvements” by the leading violin restorers of the day. However, Stradivari would be amazed to find that the modern musical world credits him with such a secret. After all, how could he possibly have had the clairvoyance to foresee that his instruments would be extensively modified in the 19th century to produce the kind of sound we value so highly today? Indeed, those sounds would have been totally alien to the musical tastes of his time!
Science has not provided any convincing evidence for the existence or otherwise of any measurable property that would set the Cremonese instruments apart from the finest violins made by skilled craftsman today. Indeed, some leading soloists do occasionally play on modern instruments. However, the really top soloists – and, not surprisingly, violin dealers, who have a vested interest in maintaining the Cremonese legend of intrinsic superiority – remain utterly unconvinced.
Maybe there is an essential aspect of violin quality that we are still failing to recognize. Many violinists say they can distinguish an instrument with a fine “Italian Cremonese sound” from one with, say, a more “French” tone, such as my Vuillaume violin. But we still do not know how to characterize such properties in meaningful physical terms.
What we need is more research, with high-quality violinists working with psycho-acousticians, scientists and sympathetic violin makers, to make further progress in solving this challenging and fascinating problem.