Scintillator dosimeters monitor radiation therapy using a scintillating material that generates light in response to irradiation; this signal is then guided via optical fibre to a photodetector. One major advantage of such a device is that it measures the delivered radiation dose over a very small volume.

“A scintillator dosimeter doesn’t affect how the dose is delivered to the target because the components used interact with the radiation the same way that water or tissue does,” explains James Archer from the University of Wollongong.

Alongside the signal-of-interest, however, Cherenkov light is generated in both the scintillator and the fibre, which can compromise the dosimeter’s spatial resolution and accuracy. The simplest way to remove this unwanted signal is to use a parallel fibre without a scintillator to measure only the Cherenkov signal and subtract it from the dosimeter signal. This approach, however, is not optimal in beams with a high dose gradient, and increases the bulk of equipment.

Instead, Archer and colleagues propose using a single probe with a signal analysis algorithm to temporally separate the Cherenkov radiation from the signal of a pulsed radiation beam (Biomed. Phys. Eng. Express 4 044003).

Analysing the tail

In a previous study, the team separated the fast rising edge of the detected signal – the Cherenkov signal – from the slow rising edge – the scintillation signal. This approach removed 74% of the Cherenkov light at the expense of only 1.5% of the scintillation signal. The main limitation here is that varying beam intensity during the pulse reduces the accuracy of determining the Cherenkov contribution.

In this latest work, Archer and colleagues investigated whether using the tail of the signal can improve the accuracy. After the radiation beam pulse has stopped, the Cherenkov signal drops off rapidly while the scintillator signal decays more slowly, enabling separation of a pure scintillation signal.

To study this premise, the researchers used a 500 µm-thick plastic scintillator optically coupled to a 10 m plastic optical fibre and read out by a photomultiplier tube. They irradiated a water tank with a 6 MV linac beam and placed the dosimeter inside to measure the delivered dose at various positions.

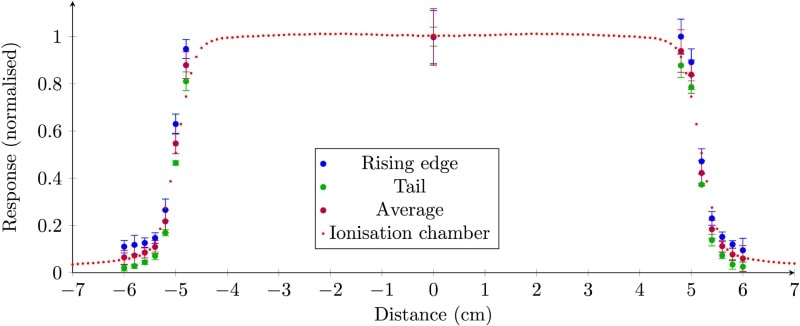
Beam profile measurements revealed that the rising edge analysis overestimated dose compared with ionization chamber measurements, while the tail-based analysis underestimated the dose. The average of the two, however, agreed well with ionization chamber results.

To quantify the differences between scintillator and ionization chamber measurements, the researchers calculated S values (the average sum of relative squared difference percentages) for a lateral beam scan at 15 mm depth, and a depth dose scan from surface to 200 mm. Using the averaged data improved the accuracy of beam profile results by 87% (to an S value of 2.20%) and depth dose results by 90% (to an S value of 0.050%).

The researchers also calculated the uncertainties in the beam profiles and depth dose results. In all cases, the tail method produced lower variations between individual measurements than the rising edge method. While the larger uncertainties in the rising edge data served to increase uncertainty in the averaged results, the authors note that there is still an advantage in combining both data sets.

“The tail of the radiation pulse provides an accurate measurement of relative dose,” explains Archer. “The rising edge analysis is slightly less accurate, but uses data from the whole pulse to determine the relative dose, and so will be proportional to the pulse duration. With these together, relative dosimetry can be done between differing pulse durations without having to measure the durations directly.”

The study demonstrated that it is possible and practical to perform single-probe temporal Cherenkov removal techniques. The team is now working on using experimental data to construct beam intensity functions that can fit to the data to the entire shape of the pulse waveform. “This provides a more accurate and more robust method to determine the exact Cherenkov contribution to the signal,” says Archer. “We have also begun working on using machine learning algorithms to learn which parts of the signal we want and don’t want.”