Measurements of the amount of lithium in the universe combined with precision data from the cosmic microwave background are challenging our understanding both of stellar astrophysics and possibly even Big Bang nucleosynthesis itself, as Kenneth Nollett explains

The nitrogen and oxygen that we breathe, the carbon that makes biochemistry possible, and the calcium in our bones have one striking thing in common: they were all synthesized inside stars. Indeed, the same is true of virtually all the chemical elements that we encounter in everyday life, from the rarest gases to the heaviest metals. One big exception is hydrogen: almost all hydrogen nuclei are protons that emerged from the Big Bang almost 14 billion years ago. Another is light nuclei such as deuterium and lithium, which were produced in a process called Big Bang nucleosynthesis that occurred when the universe was only a few minutes old. The fact that these elements have been around since the beginning of time is surely one of the most fascinating facts in astrophysics.
Big Bang nucleosynthesis (BBN) began when the universe had cooled sufficiently that protons and neutrons, which had just formed from the primordial plasma, were able to combine into deuterium nuclei. The deuterium then underwent further nuclear reactions to form helium-4 nuclei each containing two protons and two neutrons, along with tiny quantities of deuterium, helium-3 and lithium-7. Indeed, by the end of BBN (a period of a few minutes) a quarter of the ordinary matter in the universe had been converted into helium-4, while all but a minuscule fraction of the rest was left as hydrogen (see “How Big Bang nucleosynthesis works”).
Since the amounts of these nuclei produced depended on the temperatures and densities of the universe when it was just a few minutes old, we can get a handle on early cosmic evolution by measuring their abundances today (see “Observing abundances”). In particular, BBN models provide an estimate of the mean baryon density of the universe, which is a fundamental parameter in cosmology. We know from measurements of the motion of galaxies show that the total mass density of the universe is six times the baryon density inferred by BBN, which clearly indicates that most of the matter in the universe is not made of ordinary baryonic matter containing protons and neutrons but of something more mysterious called dark matter.
Such disagreement between BBN and experiment could also hint at new physical processes that may have been active during the nucleosynthesis. For example, if fundamental particles that have never been seen in the lab were present in the early universe, then their effects may be discernable in the elemental abundances we observe today. For these reasons, BBN is vital to studies of the overall structure of the universe, the history of matter since the Big Bang, and the close connection between particle physics and cosmology.
Despite its success in determining the baryon density of the universe and in explaining the large abundances of helium that we observe, BBN still faces major challenges. Recent measurements of the cosmic background radiation, which reveals the universe as it was when atoms formed about 380,000 years after the Big Bang, and of the large-scale distribution of galaxies have greatly increased the precision of cosmological data. So far it seems that the observed primordial abundances – particularly those of lithium – do not quite tally with BBN theory. The goal now is to bring BBN into line with the new precision of cosmology, and to improve our understanding of the astrophysical environments where the primordial abundances are observed.
Back in time
The first version of BBN theory was proposed by George Gamow and Ralph Alpher in the 1940s in an attempt to explain the origin of all the chemical elements. They assumed that the early universe was very hot and full of neutrons: nuclei then formed by capturing neutrons one at a time, with the occasional nucleus undergoing beta decay to produce a nucleus of higher atomic number plus an electron and a neutrino. As the probabilities of many of these reactions were not known at the time – some were even kept secret due to their relevance in atomic-weapons research – Gamow and Alpher had to guess many of their cross-sections. In doing so, however, the pair made the extremely optimistic assumption that some, then unknown, process would have a high enough probability to create nuclei larger than helium-4 – despite the fact that no stable nucleus with a mass number equal to five exists.
Gamow and Alpher’s calculations matched well the trend observed in the solar system, where nuclear abundances decrease as a function of atomic mass. Furthermore, Alpher and colleagues predicted the existence and temperature of the cosmic microwave background by realizing that a gas of hot photons would have been present during BBN. Those photons, the researchers correctly argued, would have been stretched by the expansion of space to the microwave region of today’s electromagnetic spectrum.
This early version of BBN eventually included most of the aspects of modern BBN theory, such as the role of weak interactions and the dependence of nuclear abundances on the baryon density. As a model for the origin of all the elements, however, it reached a dead end in the early 1950s when researchers recognized that a fully articulated version of this theory was doomed to make lots of helium-4 but not much else. Then in 1957 it was buried for good, when Alastair Cameron and Fred Hoyle, among others, showed that almost all of the chemical elements were, in fact, synthesized inside stars.
In 1964, however, Hoyle and Roger Tayler showed that BBN provided a simpler explanation for the large observed abundances of helium-4 than Cameron and Hoyle’s stellar explanation, since the latter required the existence of a gigantic population of now-extinct stars. When the cosmic microwave background was discovered the following year, it was immediately clear that the Big Bang model was correct and that BBN should therefore have taken place in the hot conditions of the first few minutes. Jim Peebles of Princeton University in the US responded to this discovery by performing the first “modern” calculation of BBN by using nuclear-reaction rates that were by then better known than in Gamow’s day. Although our knowledge of these rates has improved again since then, our basic understanding of BBN remains the same.
The power of BBN as a window on the early universe was recognized in the 1970s. At that time several astrophysicists, including Hubert Reeves at the Institute d’Astrophysique in Paris and Johannes Geiss, now at the International Space Science Institute in Bern, realized that because the amount of deuterium produced in BBN depended strongly on the mean baryon density of the universe, we could learn something about the universe on the largest scales by measuring the amount of deuterium much closer to home. Within a few years, several measurements of the amount of deuterium in our galaxy had set an upper limit on the baryon density of about 4 × 10–31 g cm–3.
Then in 1977 Gary Steigman, now at Ohio State University, James Gunn, now at Princeton University, and the late David Schramm of the University of Chicago showed that BBN could constrain the number of different types of neutrino that exist in nature (today we know that there are three neutrino species: the electron, muon and tau neutrinos). Each additional neutrino species, they argued, would have increased the density of the early universe and made it expand faster, thereby changing the dynamics that set the ratio of neutrons to protons at the start of BBN to favour more neutrons. This, in turn, would have led to more helium-4. At a time when laboratory measurements suggested that there might be thousands of neutrino species (although most particle physicists did not really believe there were this many), Steigman and co-workers were able to claim that there were no more than four. This was a major success for BBN theory and contributed to a growing awareness of the close links between particle physics and cosmology – even if many particle physicists saw it merely as evidence for the chutzpah of cosmologists!
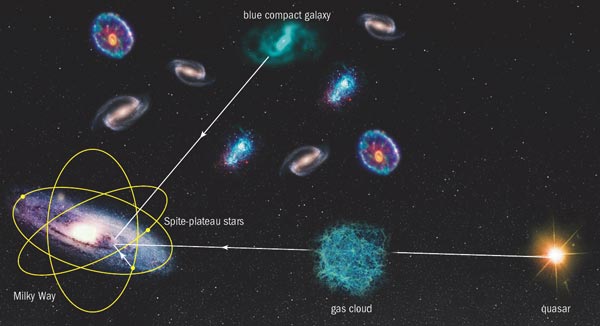
By 1982 astrophysicists had obtained good estimates of the primordial helium-4 abundance, as well as limits on the abundances of helium-3 and deuterium (see “Observing abundances”). Then François and Monique Spite at the Observatoire de Paris discovered that certain old stars in our galaxy with very thin convective envelopes – rapidly circulating regions of a star in which material is well mixed – all contained roughly the same amount of lithium-7. Since spectroscopic measurements show that stars in this “Spite plateau” contain only very small amounts of nuclei synthesized in previously existing stars, the stars must have formed out of nearly primordial gas. This meant that the amount of lithium-7 in Spite-plateau stars could be interpreted as the amount of lithium-7 synthesized during BBN.
Measurements of light-element abundances continued to advance, and by 2000 they implied a mean baryon density of 2 × 10–31 g cm–3, give or take a factor of three. On the one hand, this was a remarkable case of diverse and difficult-to-obtain data all converging to some value. On the other hand, the formal error bars reflecting known sources of uncertainty had become so small that the data points technically disagreed with one another. While it was easy to imagine further systematic errors that could bring the results closer together, due either to the observational techniques or to effects involving the history of the material being observed, it was much harder to quantify them.
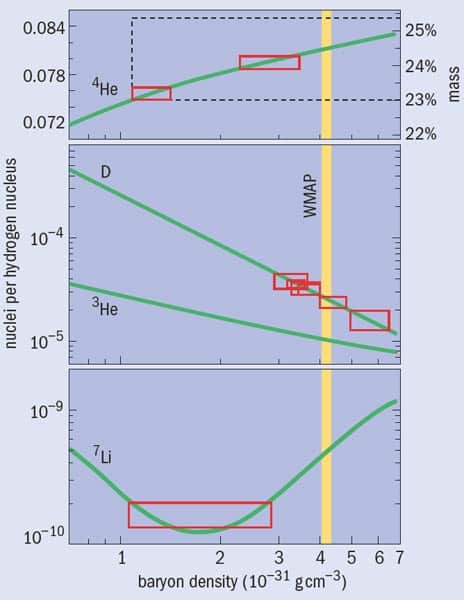
Measurements of deuterium in distant concentrations of gas lying between us and even more distant quasars favoured a mean baryon density of about 4 × 10–31 g cm–3, while the simplest interpretation of the lithium plateau and some of the helium-4 data favoured values nearer 1 × 10–31 g cm–3 (see “Measuring up to data”). As for the primordial abundance of helium-3, the post-BBN history of these nuclei is too uncertain to be able to constrain the mean baryon density. This disagreement prompted a vigorous programme of research by several groups in an attempt to improve the measurements and resolve the remaining discrepancies. In the mean time, however, precision cosmological data had started to give BBN a run for its money.
Elemental light
By the early 2000s, in the midst of the often heated debate over what to make of the different abundance measurements, BBN was no longer the only way to determine the mean baryon density of the universe. In 1992 the COBE satellite revealed that the temperature of the cosmic microwave background varies by a few tens of microkelvin on angular scales of 5° or more, thus providing evidence for density fluctuations in the early universe that may have seeded cosmic structure. Then in 2000 the BOOMERANG and MAXIMA experiments detected fluctuations on angular scales smaller than 1°. A key prediction of Big Bang theory, these fluctuations are the imprints left by acoustic waves that propagated through the plasma just before neutral hydrogen atoms first formed, some 380,000 years after BBN when the cosmic microwave background was born. And since the properties of the plasma depend on the baryon density, the amplitudes of these fluctuations provided the first strong independent crosscheck of the baryon density predicted by BBN.
The initial BOOMERANG and MAXIMA results favoured a higher baryon density than the BBN value: (6.0 ± 2.0) × 10–31 g cm–3. However, combined with the more recent data from the Wilkinson Microwave Anisotropy Probe (WMAP) – which measured temperature fluctuations on scales down to 0.3° – the current most precise value is (4.1 ± 0.1) × 10–31 g cm–3. While this independent measurement settled an ongoing debate within the BBN community over the value of the baryon density, it brought the issue of systematic uncertainties in BBN into sharper focus (see “Measuring up to data”).
For example, the baryon densities inferred from the WMAP data and from measurements of the primordial deuterium abundance agree very closely. But the primordial deuterium abundance has been measured in only eight locations so far; and although the results all cluster around a value of 3 × 10–5 per hydrogen atom, their dispersion around that average is wider than would be expected given their error estimates. Such a variation with location is not what one would expect from BBN, which should have happened in the same way everywhere according to Big Bang theory. We probably need more data in order to understand this slight discrepancy, but this is easier said than done because the only way to identify and measure the primordial deuterium abundance is to spend huge amounts of observing time on the world’s largest telescopes.
There are similar discrepancies between BBN theory and the primordial helium-4 abundance. Unlike the deuterium abundance, the amount of helium-4 produced in the BBN model increases very slowly as a function of the mean baryon density of the universe, which means it has to be measured with a precision of a few per cent to be useful for BBN studies. To do this, astronomers study the brightness of certain spectral lines emitted by atoms in a plasma in a distant galaxy, from which they can derive a consistent set of parameters that characterize the plasma (see “Observing abundances”). Different research groups tend to use slightly different sets of lines to determine these parameters and they handle data in different ways. Somewhat disconcertingly, different groups have produced conflicting results.
In the 1990s the largest difference was between the results of Yuri Izotov at the Academy of Sciences of the Ukraine and Trinh Thuan at the University of Virginia in the US (right-hand, larger box in “Measuring up to data” figure) and a larger data set compiled by Steigman with Keith Olive and Evan Skillman of the University of Minnesota based on earlier observations (left-hand box). However, it is likely that the uncertainties of both approaches have been underestimated and that the discrepancy lies somewhere in a laundry list of small corrections such as how much light is scattered by dust between us and the plasma. The allowed range of the helium-4 abundance therefore probably spans the results of both groups (dotted box in “Measuring up to data”). Again, more precise observations may be needed, or perhaps we require a fundamental change of approach to find a solution with which everyone can agree.
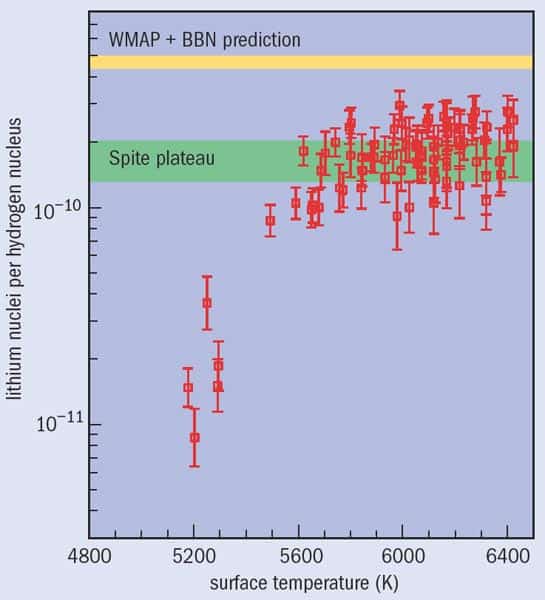
Today the biggest mysteries of BBN involve lithium. For the baryon density provided by WMAP, BBN predicts that there are 4.7 × 10–10 lithium-7 atoms for every hydrogen atom, while the Spite-plateau stars contain only about 1.4 × 10–10. Several explanations for this discrepancy have been proposed, but no-one knows the right answer. Either some important physical process is missing from BBN theory, some astrophysical mechanism destroys large amounts of lithium-7 after BBN, or there is something is wrong with our interpretation of stellar spectra.
The problem with lithium
To solve the lithium mismatch, some physicists have turned their attention to BBN models that incorporate exotic ideas from particle physics. Many theories that seek to unify the fundamental forces in nature – most popularly based on supersymmetry or on models with extra space–time dimensions – predict the existence of heavy particles not yet seen in the laboratory. If these particles were unstable and decayed within a year after BBN, they may have produced large effects on the nuclear abundances by providing neutrons, protons and energy for a second round of nucleosynthesis involving different reactions at much higher energies.
In one example, last year Jonathan Feng at the University of California at Irvine and co-workers proposed such a model whereby “normal” supersymmetric particles such as neutralinos (the supersymmetric partners of force-carrying particles like photons and Z bosons) decay to form particles called superWIMPs, which may constitute present-day dark matter. But many variations are possible as long as the decay products include protons, neutrons and photons. The energetic particles created in the massive-particle decays interact with the BBN nuclei created months earlier. In this way, particles with appropriate masses and decay properties can destroy two-thirds of the beryllium-7 produced intermediately during BBN, and since beryllium-7 nuclei decay after BBN to produce the primordial lithium-7, Feng’s proposal could provide a neat solution to the lithium shortfall.
The hope underlying such exotic particle-physics models is that the lithium problem might provide the first sign of some new fundamental physics. BBN studies could then guide accelerator experiments such as those at the upcoming Large Hadron Collider at the CERN particle-physics lab. Unfortunately, BBN does not offer enough information to do this decisively, other than delineating what is possible and impossible. Indeed, most researchers in the field of light-element abundances would probably favour more mundane solutions to the lithium problem, even if such solutions are less interesting to particle physicists.
Answers from astrophysics
One such alternative possibility is to tweak the thermal models of the atmosphere of a star that are used to infer its composition from observations. For example, in 2004 Jorge Meléndez, now of the Australian National University, and Iván Ramírez of the University of Texas claimed that the models for the Spite-plateau stars depend on poor estimates of the stellar surface temperatures, and proposed a severe “rescaling” of these estimates that shift the lithium measurement towards agreement with the WMAP data. This proposal has met with much scepticism from colleagues, however, mainly because the rescaling procedure leads to temperatures that disagree with other measurements such as the intensities of hydrogen emission lines. In any case, rescaling can at best only be a partial solution to the lithium problem, since it only raises lithium abundances by a factor of 1.4 – not the factor of three required.
Perhaps the most likely explanation for the apparent lack of lithium is that the stars we observe have been gradually destroying their lithium over the 10 billion years or more since they formed. Astronomers can only observe the outside of a star – the top of the convective envelope. However, any lithium in a star that is exposed to temperatures above about 2.5 × 106 K is rapidly destroyed by the nuclear reaction 7Li + H → 24He. Therefore, lithium can only be completely preserved in the convective envelope if the whole envelope is too cold to burn it, and if lithium is not mixed between the surface layer and the deeper, hotter layers of the star. Although the Spite-plateau stars have been chosen to satisfy these criteria, there could be unexpected processes going on inside them.
But how could lithium on the surface of a star be mixed from the surface zone into the stellar interior? Several mechanisms are known that could potentially mix the convecting and non-convecting parts of stars, but it is difficult to compute the rates of these processes from first principles. The most stringent constraint on a mixing model is that it must maintain the observed tight bunching of plateau stars that have the same average lithium-7 abundance (see “The lithium discrepancy”).
In a series of papers that was published between 2002 and 2004, Olivier Richard and collaborators at the Université de Montréal in Canada proposed such a mixing model that has since gained observational support. It suggests that all nuclei heavier than hydrogen settle very slowly out of the convective envelope under the action of gravity. In particular, the model makes specific predictions for settling as a star evolves, which are revealed as variations of surface composition as a function of mass in stars that formed at the same time.
By spring 2006, Andreas Korn of Uppsala University in Sweden and colleagues had used the European Southern Observatory’s Very Large Telescope (VLT) in Chile to study 18 chemically primitive stars in a distant globular cluster called NGC 6397 that were known to have the same age and initial composition. From this the researchers showed that the iron and lithium abundances in these stars both varied according to stellar mass as predicted by Richard’s model. In fact, the model indicated that the observed stars started out with a lithium abundance that agrees with the WMAP data. Corroboration of these results is vital because if the result stands up to scrutiny based on a wide range of data, then we have solved the lithium problem.
Looking for lithium-6
Another way to determine the amount of lithium-7 destroyed in stars is to observe the element’s other, less stable, isotope: lithium-6. Lithium-6 is not made in detectable quantities by BBN but instead comes from collisions between nuclei in cosmic rays and in the interstellar gas. Since lithium-6 is even more easily destroyed than lithium-7, detecting it allows us to place limits on the destruction of lithium-7.
In 2006 Martin Asplund and co-workers at the Mount Stromlo Observatory in Australia made extensive observations of lithium-6 in plateau stars using the VLT. In each of the nine stars where they found lithium-6, roughly 5% of the lithium consisted of this isotope – which was larger than expected although at the limit of what was detectable with the equipment. This has huge implications not only for BBN but also for the history of cosmic rays in the galaxy and for stellar astrophysics. For example, the production of such large amounts of lithium-6 must have required an enormous flux of cosmic rays early in the history of our galaxy, possibly more than could have been provided by known acceleration mechanisms. Moreover, if the plateau stars have truly destroyed enough lithium-7 to bring the WMAP prediction of the mean baryon density into agreement with that obtained with the observed Spite plateau, the greater fragility of lithium-6 implies that the stars initially contained lithium-6 in quantities comparable to the observed lithium-7 plateau.
All of these facts make the lithium-6 observations an uncomfortable fit for BBN, stellar physics and models of cosmic-ray nucleosynthesis – particularly since the production of large amounts of lithium-6 via cosmic rays has to be accompanied by a similar production of lithium-7. Although lithium-6 can be produced in some of the exotic particle-physics scenarios mentioned earlier, it is vital that we independently confirm Asplund’s results. Indeed, the hunt for primordial lithium (of both isotopes) is currently ongoing at the VLT, as well as at the Keck Observatory and the Japanese Subaru Telescope, both in Hawaii. Although such observations are right at the limit of what can be achieved with these instruments, the pay-off could be enormous: if the lithium-6 results stand, we will require an extensive re-examination of what we think we know about stars, cosmic rays and BBN.
Window on the early universe
Better measurements of the primordial abundances combined with precise cosmological data are leading to a shift in the way BBN is studied. Within their estimated errors of about 10%, the abundances of helium-4, deuterium and lithium-7 disagree with BBN theory. But within the “believable” range of poorly quantified additional uncertainties, such as those arising from our ignorance of certain astrophysical environments, the measurements tell us that BBN is correct.
Our task now is to remedy that ignorance and, if discrepancies persist, to figure out what that means for the physics of the early universe. Even if the lithium problem turns out to be an early sign of new particles or other fundamental physics, a definitive answer will still depend on a better understanding of the Spite-plateau stars. In other words, it would be prudent to exhaust all astrophysics explanations before overhauling BBN based on as-yet-undiscovered fundamental physics.
For nearly three decades BBN was the linchpin in the argument for non-baryonic dark matter in the universe. It remains our clearest window on the universe for times less than a year after the Big Bang and – through its measurement of the baryon density – an important crosscheck of the cosmological data provided by both the microwave background and surveys of galaxy distributions. However, now that the cosmic microwave background has provided more precise measures of the mean baryon density than BBN, largely due to WMAP, the role of BBN in astrophysics is changing.
The new situation has increased the number of constraints on BBN, potentially improving its strength as a test of particle-physics models. Indeed, the first test for any extension to the Standard Model of particle physics is that it preserves the even incomplete success of BBN. In the next few years, projects like the follow-up to the Sloan Digital Sky Survey, SEGUE, and the RAVE programme at the Anglo-Australian Observatory will measure the compositions of roughly a million stars in our galaxy. This large sample of stars with diverse ages, compositions and histories will be used to reconstruct the tangled histories of the assembly of our galaxy and of its atomic nuclei, much as palaeontologists use fossils to reconstruct the history of life on Earth. BBN provides the initial setting for this story of our origins.
More about: Big Bang nucleosynthesis
M Asplund et al. 2006 Lithium isotopic abundances in metalpoor halo stars Astrophys. J. 644 229–259
T Beers and N Christlieb 2005 The discovery and analysis of very metal-poor stars in the galaxy Ann. Rev. Astron. Astrophys. 43 531–580
A Korn et al. 2006 A probable stellar solution to the cosmological lithium discrepancy Nature 442 657–659
D Lambert 2004 Lithium in very metal-poor dwarf stars – problems for standard Big Bang nucleosynthesis? arXiv:astro-ph/0410418v1
D Schramm and M Turner 1998 Big Bang nucleosynthesis enters the precision era Rev. Mod. Phys. 70 303–316 BBN site: bigbangonline.org
At a Glance: Big Bang nucleosynthesis
- Big Bang nucleosynthesis (BBN) is the process during which the light nuclei deuterium, helium-3, helium-4 and lithium-7 were produced in the first few minutes of the universe
- For many years BBN provided the most reliable way to determine the mean baryon density of the universe – a central parameter in cosmology that revealed that the universe is mostly made of “dark” matter rather than ordinary protons and neutrons
- A major component of the hot Big Bang model, BBN can be tested by measuring the abundances of certain light nuclei present in very old cosmic material
- Current measurements of the abundances of light nuclei give inconsistent values for the baryon density of the universe, with lithium in particular challenging our understanding of both the stars in which it is observed and of BBN theory itself
- Precision measurements of the cosmic microwave background provide an independent measure of the baryon density, and allow more stringent tests of the BBN model