When CERN’s Large Hadron Collider failed to uncover evidence of new “superpartner” particles during its first run, some claimed that the theory that predicts them – known as supersymmetry, or SUSY – should be abandoned. S James Gates, Jr, however, argues that giving up on SUSY now would be like concluding that giant sequoia trees do not exist after surveying only the east coast of North America, and that there is more at stake than meets the eye
As a theorist, I keep a “bucket list” of the phenomena I would most like to see observed in nature before I am shuffled off this mortal coil. Not long ago, my bucket list looked like this:
- a Higgs boson;
- gravitational waves;
- superpartner particles;
- direct evidence supporting superstring/M-theory.
The discovery of a Higgs boson in experiments at CERN’s Large Hadron Collider (LHC) was, of course, the joyous fulfilment of the first item on my list. Recently, it seemed I might be able to cross gravitational waves off as well, when scientists in the BICEP2 collaboration reported observing the imprint of these waves in the cosmic microwave background. Since then, a few flies have appeared in the stew, so to speak, but I would still be surprised if we do not see evidence of gravitational waves within a decade. As for evidence supporting string theory, in my view this is not as unlikely as some critics have argued, but I accept that it is far more of a long shot.
But what about the third item on the list? Superpartner particles or ‘‘sparticles’’ are predicted to exist under an extension of the Standard Model of particle physics that makes use of the principle of supersymmetry (or SUSY). SUSY is not a single model any more than Newton’s second law is a rule that applies solely to falling apples. Instead, SUSY is a framework for many models; indeed, this adds to the complication of its discovery. Collider searches can only strive to observe the predictions of models. Even under many reasonable assumptions, numerous such models remain possible. Ruling out one or a few does not exclude a far greater multitude of others.

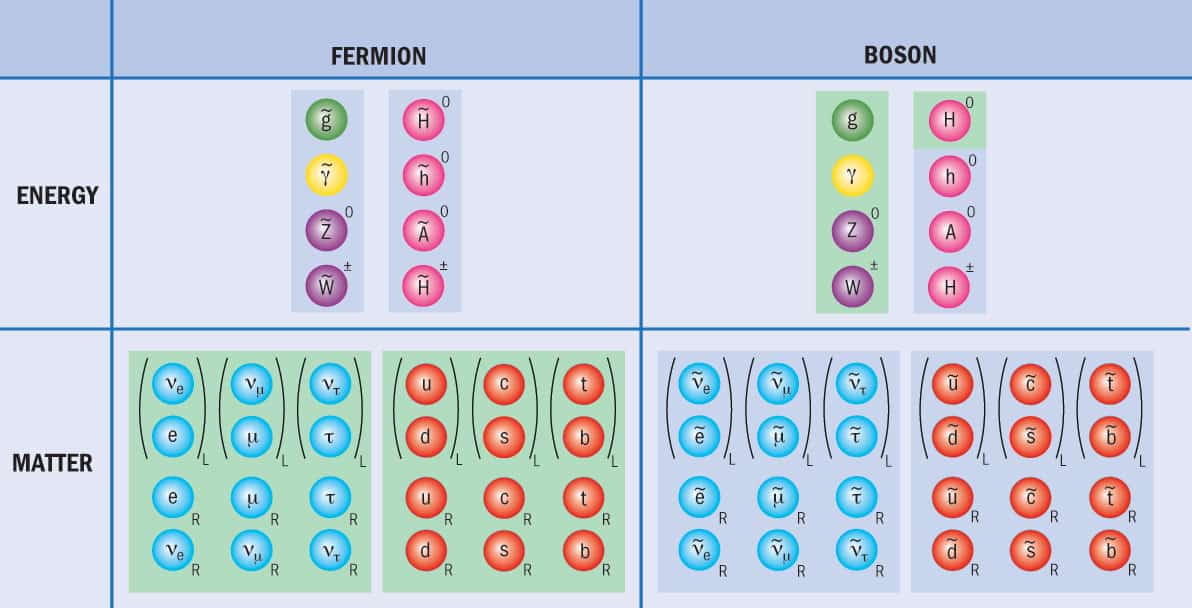
The common factor in all SUSY models is a prediction that each of the observed fundamental particles in the Standard Model has at least one very similar “twin” that differs from known particles only in mass and quantum spin. For example, the known force-carrying bosons (the photon, gluons, W and Z particles) all have quantum spins equal to one, so their sparticle twins must be fermions, which have spins equal to one-half. Similarly, the matter particles – electrons, neutrinos, quarks and so on – are all spin one-half fermions, so their sparticle twins must be bosons with spin equal to zero. Figure 1 shows the increase in particles that would occur, as a minimum, if a supersymmetric version of the Standard Model was found to describe nature.
In the years before the LHC was switched on in 2008, many physicists theorized (and rhapsodized) about the ease with which sparticles would be discovered in LHC collisions. So far, though, sparticles have been conspicuous by their absence. This has led to a “SUSY is dead” meme being promulgated among many interested parties – aided, perhaps, by the unreasonable expectations created ahead of the switch-on. My own views, however, have always been more cautious. In fact, in 2006 I publicly lamented the irrational exuberance that seemed to have swept the particle-physics community about the likelihood of early detection of SUSY. These views were disregarded, but – like the predictions of Cassandra in Greek mythology – they proved to be accurate. Now, as the LHC is being prepared to return to active operations, I welcome the opportunity to comment once more on the prospects for discovering SUSY at work in nature.
As with the hypothetical hunt for giant sequoia trees, finding evidence for SUSY depends on the observer looking in the right place
In my view, the current situation is akin to that of an explorer who, having scoured the eastern seaboard of North America, concludes that no groves of Sequoiadendron giganteum exist in the entire continental USA. As with this hypothetical hunt for giant sequoia trees, finding evidence for SUSY depends on the observer looking in the right place. My aim in this article is to explain why, despite the difficulty, the search for SUSY continues to be worthwhile, and why I disagree with colleagues who believe that it will never be found as an accurate description of nature. There is more of an issue than simply finding a SUSY model: the physics definition of the quantum vacuum state is also at stake.
The taming of the vacuum
To appreciate the attraction that SUSY holds for theorists, it helps to understand the theory’s history. Today it is often forgotten that SUSY did not emerge to answer problems in our understanding of nature or the Standard Model. Instead, it emerged in the 1970s from “blue sky” considerations of the mathematical properties of relativistic quantum field theory (QFT).
At the time, it was thought that all possible symmetries that could exist in QFT had already been enumerated. Indeed, a 1967 result called the Coleman–Mandula theorem had essentially asserted that physicists already knew all there was to know about symmetries, at least at the mathematical level. However, the theorem had a hole in it, and in 1971 two Soviet-era physicists, Yuri Gol’fand and Evgeny Likhtman, exploited this hole to discover a new possibility: a symmetry hidden in the mathematics of QFT that relates fermions to bosons and vice versa.
Gol’fand and Likhtman worked during a time when the Iron Curtain inhibited communication, and their discovery was essentially unknown in the West. A few years later, however, SUSY had a Western emergence thanks to Julius Wess and Bruno Zumino, who investigated the possibilities of mathematical symmetries between fermions and bosons in response to some studies (by Jean-Loup Gervais and Bunji Sakita) of the mathematical properties of early models of string theory. This new fermion–boson symmetry eventually became known as “supersymmetry”.
At this stage, theorists found supersymmetry attractive because it seemed almost magically to ameliorate a notoriously difficult problem with QFT. To get a feel for this problem, here is an analogy. Imagine blowing on the surface of a bowl of still water. Even if you blow very gently, you will still produce waves that can be seen to move across the surface. Now imagine carrying out the same action, but not too closely, with a pot of vigorously boiling water. In this scenario, it would be difficult to detect the waves created by your gentle blowing because the activity of different sizes of bubbles coming to the surface would tend to obscure them.
This is the essential problem of QFT. In a quantum universe, the lowest state of energy – the vacuum – is not empty. Instead, it is like the surface of the boiling liquid, with “virtual particles” that pop in and out of existence like bubbles. Hence, to describe the vacuum mathematically, we need a way to subtract the motions caused by the behaviour of the virtual particles. But ordinarily, the way theorists define the vacuum state in QFT is ambiguous. This ambiguity is most pointedly seen in a theoretical approach known as the “canonical method of second quantization”. So what is this ‘‘second quantization’’ about? Well, the ‘‘first quantization’’ is the one that replaced the Newtonian concept of the particle with the concept of wave–particle duality and used wavefunctions to describe particle behaviour mathematically. But within this first, familiar quantization, the number of equivalent particles described by wavefunctions is not allowed to change. This runs into a problem as it does not allow these equivalent particles to decay into others. What second quantization does is to fix this by extending the mathematics in a way that allows for the kind of particle creation and annihilation that takes place constantly in the vacuum.
When deriving the descriptions of the energy states associated with a QFT using the second quantized method, there comes a point at which one must ignore the existence of a certain constant, which has a value of infinity, in order to make numerical predictions. Ignoring infinities might seem like a bad idea, but in the 1950s, Richard Feynman, Sin-Itiro Tomonaga and Julian Schwinger showed that this piece of mathematical legerdemain is, in fact, possible. Their method is known as “renormalization” and it yields results that agree, to better than one part in a billion, with experimental data. In 1965 they were rewarded with the Nobel Prize for Physics.
Sweeping infinities under the rug through renormalization made theorists uncomfortable, which is where SUSY entered the picture
Despite the fantastic success of renormalization, the process of “sweeping infinities under the rug” has long made theorists uncomfortable. Some began to search for alternatives, and this is where SUSY first entered the picture. It turns out that renormalization is a requirement of all known QFTs, except those with the property of SUSY; QFTs with a SUSY component require fewer (and some even no) such procedures. Only SUSY QFTs have a well-defined vacuum state and this is because of supersymmetry.
Throughout the 1970s, the link between SUSY and the renormalization problem drove much of the interest in the theory. The shift came in the early 1980s when members of several theoretical collaborations pointed out that the mathematics describing a particle–sparticle pair could be consistent even if the members of the pair had different masses. They arrived at this result by borrowing mathematical concepts that are essentially the same as those in the Higgs boson construction, and the effect on the theoretical community was significant; many people with no previous involvement in SUSY suddenly became very, very interested.
This shift in thinking was the genesis of the theory we now call the minimal supersymmetric Standard Model (MSSM). This mathematical construction is called “minimal” because it consists of the particles of the well-established Standard Model together with the minimal number of sparticles required by SUSY. Later, theorists also proposed a “next to minimal” supersymmetric Standard Model (NMSSM) that includes more undiscovered particles and sparticles, and other flavours of SUSY predict an even richer sparticle world. At this point – and not before – the Standard Model became part of SUSY’s story.
Gaps in the Standard Model
These historical notes show that it is inaccurate to regard SUSY as having been “invented” to solve problems with the Standard Model. However, from today’s perspective, some of the most prominent reasons for continuing to explore SUSY do indeed stem from attempting to fill gaps in the model. The Standard Model is like a finely wrought instrument, but it is silent on topics such as why the values of masses, mixing angles and coupling constants are what we measure them to be, and why distinct particles exist in such profuse numbers.
One of the most commonly cited problems with the Standard Model is that it lacks a compelling reason to introduce new elementary particles, such as WIMPs (weakly interacting massive particles), that could account for the behaviour of dark matter. The presence of so many superpartners in the MSSM provides a logical – indeed almost compelling – solution to this problem (see “Theories of the dark side”, July 2014).
1 Filling the gaps
This “periodic table” for matter particles and force carriers shows how SUSY theory expands the Standard Model by predicting fermionic partners (top left) for known bosons like the gluon, photon, Z and W particles (top right), along with bosonic partners (bottom right) for known fermions like the electron, muon and tau, the three neutrinos and the six quarks (bottom left). SUSY also predicts that the Higgs boson discovered at CERN is only one of at least five such bosons to exist in nature. These additional bosons (and their superpartner equivalents) are believed to have much higher masses than that of the “plain vanilla” Higgs. The L and R subscripts indicate that these particles (and antiparticles) are associated with left- or right-handed spin. Particles not yet detected lie on a blue background.
Another flaw with the Standard Model is that it does not provide any insight into the “gauge hierarchy” problem in QFT. This is a more technical issue, and it concerns how the coupling strengths of the three forces in the Standard Model – the electromagnetic force, the weak nuclear force and strong force – vary with distance. For example, the strong force, which is described by quantum chromodynamics (QCD), is responsible for binding quarks together to form protons and neutrons. If the distance between two quarks is approximately the radius of a neutron (0.3 × 10–15 m), then the coupling constant for this force, gs, is about 2.49. (You can think of gs as the QCD force’s equivalent of the electric charge in electromagnetism.) But if the distance between two quarks shrinks to one-tenth of the neutron’s radius, gs falls to about 1.48. This means that the closer quarks are to one another, the weaker the QCD force is that attracts them, and vice versa.
The phenomenon of the changing value of coupling constants is known as “running coupling constants”, and the discovery of its effect in QCD resulted in a Nobel prize being awarded to David Gross, David Politzer and Frank Wilczek in 2004. It occurs because in QFT, matter particles (such as the two quarks in this example) are always bathing in the sea of virtual particles that pop out of the vacuum (this was alluded to earlier with the “boiling surface” analogy). The presence of these virtual particles changes the forces to which the observable particles are subject, just like adding salt to pure water changes the buoyancy force. Their effect is distance-dependent, and whether the coupling constants get larger or smaller as the particles get closer together depends on the force studied. Forces that become weaker with decreasing distance are said to possess ‘‘asymptotic freedom’’. By the same token, these forces must become stronger with increasing distance, a phenomenon known as “infrared slavery”.
Changes to the coupling constants at very small distances are important because, within the context of QFT, investigating what happens at small distances corresponds to investigating systems with very high energies. Our universe is one such system, and the moment when its energy density was greatest occurred around the Big Bang. The “running coupling constants” scenario implies that in the very early universe, the coupling constants, which characterize the three forces of the Standard Model, must have had very different values than they do now. Moreover, at times near the Big Bang, the differences in the masses of the bosons that carry these three forces became negligible. The reason for this is that the average energy in any location was, at that time, enormous. Thus, according to Einstein’s mass–energy equivalence, the masses of all of the Standard Model force-carrying particles (which all have spin-1) would have been tiny compared with the energy in the environment surrounding them, and we can ignore their comparatively tinier mass differences in such conditions.
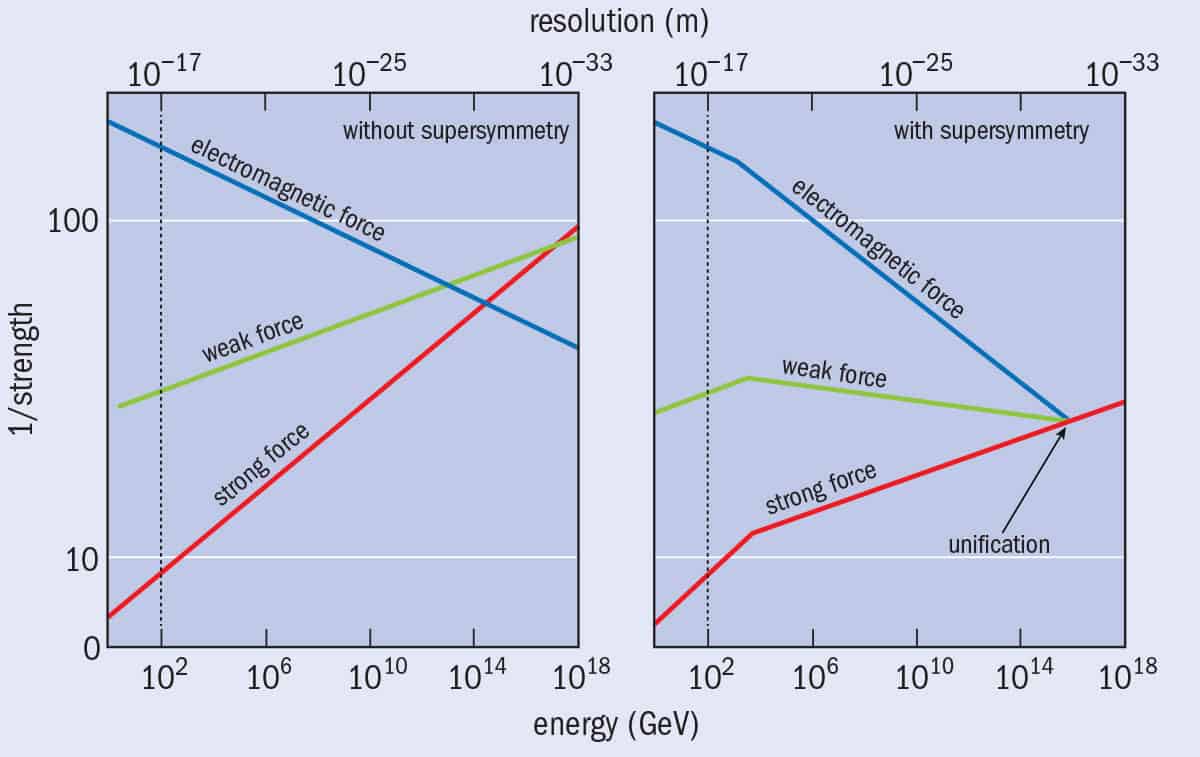
Using the machinery developed by Sheldon Glashow, Helen Quinn and Steven Weinberg, one can explore the behaviour of the coupling constants in this high-energy regime according to the Standard Model and compare it with the behaviour expected if the Standard Model had a SUSY extension. In the basic Standard Model, there is no single energy at which all three constants join together to have the same value, but when a SUSY component is added, unification – meaning the point when they all have the same value – occurs at an energy of about 1016 GeV (figure 2). Thus, including SUSY implies that the single force uniting the QCD, electromagnetic and weak force near to the time of the Big Bang would have undergone a single transition later, becoming three distinct forces (a discovery made by Savas Dimopoulos, Stuart Raby, and Frank Wilczek).
2 To unify, or not to unify uniquely
The strengths of the coupling constants of the electromagnetic, strong and weak nuclear forces vary with the distance between particles (top scale) and, equivalently, with energy (bottom scale). In the low-energy world we see around us, and even in the higher-energy conditions produced in the current generation of particle colliders (dashed line), the values of these coupling constants differ. SUSY theory predicts that their values will converge, or unify, at an energy of about 1016 GeV (right). But without SUSY, the convergence does not occur (left) at a single point.
The final major complaint made about the Standard Model is that it is not “natural”. A useful way of thinking about what “natural” means in this context (and one I am borrowing from Tristan Hubsch of Howard University) is to imagine flipping a coin and observing how it lands. The “natural” expectation is that the result will be either “heads” or “tails”, but there is also a very small possibility that the coin will land on its edge and stay there. This would be a very “unnatural” outcome though, and if it occurred repeatedly, one would become suspicious that something else was going on.
Within the Standard Model, the observed mass of the Higgs boson is a bit like the coin landing on its edge; its mass seems unnaturally light when compared with all of the possible mathematical outcomes allowed in the model. The reason this lightness seems “unnatural” is to do with the fact that the Higgs boson (unlike all of the other elementary bosons we know about) is a spin-zero particle, and the mass of such particles is affected in a unique way by quantum fluctuations associated with the virtual particles mentioned earlier. Theorists like me worry about how the mass of a light Higgs boson can be stable in the face of these quantum fluctuations; although such stability is mathematically possible, within the Standard Model it is about as likely as a coin landing on its edge after many flips. However, if we add SUSY to the Standard Model, then the mathematics becomes technically “natural” – as if you made the coin balance on the edge by putting your finger on top and holding it there.
The serendipity quotient
If we accept these arguments about dark matter, gauge hierarchy and naturalness, then the Standard Model as currently conceived must be incomplete. But these phenomenological factors are not the main reasons that I support further investigations into SUSY. For me, the most important benefit of supersymmetric theories is the same one that got me excited about them back in the 1970s: they are the only QFTs that treat the quantum state with the lowest possible energy in an elegant way.
This brings me to a property I call the “serendipity principle”. Reality is both self-consistent and filled with extraordinarily large numbers of apparent coincidences. Accurate theories of nature should, I believe, also have these qualities. This guiding principle suggests that, given two formal mathematical approaches to describing a physical system (and in the absence of clear observational or experimental guidance), the approach that supports the largest number of robust, unexpected and serendipitous relations is the one most likely to provide a path for continued progress in the long run.

The three problems I described in the previous section – dark matter, gauge hierarchy and “naturalness” – are all examples of SUSY’s high serendipity quotient. There are, of course, many others. One of the first examples of the serendipitous use of SUSY concepts was discovered by Edward Witten in 1981. In a universe described by Einstein’s general theory of relativity, energy must always be a positive quality, and Witten showed this was true via a mathematical proof using SUSY. Prior to this no such proof had ever been found for general relativity.
Another example concerns the possible extension of something similar to quark–lepton symmetry. This occurs between quarks and the family of particles known as leptons, which includes the electron and its heavier cousins, the muon and the tau. When this symmetry – which explains why pairs of leptons appear in the Standard Model alongside pairs of quarks – is applied to a version of the Standard Model that possesses SUSY, the implication is that the Higgs boson discovered at the LHC is not the only one. Instead, there must be a minimum of five Higgs bosons. This might seem like an embarrassment of riches, but if at some future point a second Higgs boson is observed, it could be a sign of SUSY appearing in nature. (There are other mathematical explanations for multiple Higgs bosons, but in the absence of SUSY, these other explanations would come at the price of signalling that there are more forces in nature than we know about already.) The detection of these additional Higgs bosons could be difficult because most SUSY models predict that their masses would be considerably heavier than the “plain vanilla” Higgs boson found in the Standard Model. Still, one can be optimistic that, at some point, it might be possible to detect them.
Quo vadis, SUSY?
Only careful observation of nature can bring the clarity needed in this field. As experimentalists at the LHC prepare for upgraded operations in the next year, they will take the lead in settling the question of SUSY. At the same time, we need to be alert to the work of scientists who are looking for indications of SUSY elsewhere in the cosmos, particularly those involved in the continued search for dark matter as well as other possible astrophysical anomalies. And of course, we theorists will continue, as we have done for decades (and with results applicable outside of SUSY, as in the example of Witten’s work), to develop new tools to enhance our ability to probe the Standard Model and QFTs.

Ultimately, our science demands both patience and scepticism. In discussing the possibility that SUSY could be an accurate description of nature, neither “irrational exuberance” nor “irrational pessimism” should prevail. We as a community need to exercise particular probity in this because extreme views do a disservice to science among the general public, and we can only thrive with public support. The cancellation in 1993 of the US’s Superconducting Super Collider, with which we could have discovered the Higgs boson (and much else) more than a decade ago, stands as a stark warning of the need for clarity, discipline and an ability to enunciate clearly how our drive to understand nature fits within national and international aspirations.
Yet while faith is no substitute for observation in science, I remain convinced (to misquote Mark Twain) that the reports of SUSY’s death have been greatly exaggerated. If the universe is not supersymmetric at some fundamental level, it will mark the first time in several centuries when symmetry has failed to be a reliable guiding principle in uncovering the mysteries of our universe. Although this could happen, I suspect it will not. In the words of one early SUSY theorist, Peter van Nieuwenhuizen, “We hope that nature is aware of our efforts.” In the end, the property of the SUSY principle that gives me the greatest confidence that it will be vindicated in the long run is its remarkably distinct properties in taming the behaviour of quantum fluctuations compared with all other versions of QFT ever discovered. It is this power, indicated by taming the vacuum, that suggests there is something unique about supersymmetrical QFT theories. For a theorist of my generation, the question of why the QFT vacuum is more stable for SUSY theories harkens back to a similar question asked at the turn of the 19th century: ‘‘Why is the ground state of the hydrogen atom stable?’’