The attractive force between two surfaces in a vacuum - first predicted by Hendrik Casimir over 50 years ago - could affect everything from micromachines to unified theories of nature.
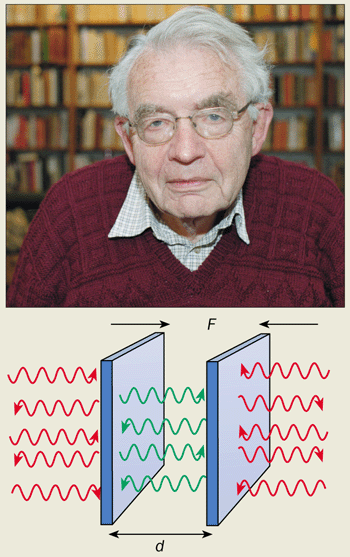
What happens if you take two mirrors and arrange them so that they are facing each other in empty space? Your first reaction might be “nothing at all”. In fact, both mirrors are mutually attracted to each other by the simple presence of the vacuum. This startling phenomenon was first predicted in 1948 by the Dutch theoretical physicist Hendrik Casimir while he was working at Philips Research Laboratories in Eindhoven on – of all things – colloidal solutions (see box). The phenomenon is now dubbed the Casimir effect, while the force between the mirrors is known as the Casimir force.
For many years the Casimir effect was little more than a theoretical curiosity. But interest in the phenomenon has blossomed in recent years. Experimental physicists have realized that the Casimir force affects the workings of micromachined devices, while advances in instrumentation have enabled the force to be measured with ever-greater accuracy.
The new enthusiasm has also been fired by fundamental physics. Many theorists have predicted the existence of “large” extra dimensions in 10- and 11-dimensional unified field theories of the fundamental forces. These dimensions, they say, could modify classical Newtonian gravitation at sub-millimetre distances. Measuring the Casimir effect could therefore help physicists to test the validity of such radical ideas.
| Casimir and colloids |
| The fact that an attractive force exists between two conducting metal plates was first predicted in 1948 by Hendrik Casimir of Philips Research Laboratories in the Netherlands. At the time, however, Casimir was studying the properties of “colloidal solutions”. These are viscous materials, such as paint and mayonnaise, that contain micron-sized particles in a liquid matrix. The properties of such solutions are determined by van der Waals forces – long-range, attractive forces that exist between neutral atoms and molecules.
One of Casimir’s colleagues, Theo Overbeek, realized that the theory that was used at the time to explain van der Waals forces, which had been developed by Fritz London in 1932, did not properly explain the experimental measurements on colloids. Overbeek therefore asked Casimir to investigate the problem. Working with Dirk Polder, Casimir discovered that the interaction between two neutral molecules could be correctly described only if the fact that light travels at a finite speed was taken into account. Soon afterwards, Casimir noticed that this result could be interpreted in terms of vacuum fluctuations. He then asked himself what would happen if there were two mirrors – rather than two molecules – facing each other in a vacuum. It was this work that led to his famous prediction of an attractive force between reflecting plates. |
Understanding the Casimir force
Although the Casimir force seems completely counterintuitive, it is actually well understood. In the old days of classical mechanics the idea of a vacuum was simple. The vacuum was what remained if you emptied a container of all its particles and lowered the temperature down to absolute zero. The arrival of quantum mechanics, however, completely changed our notion of a vacuum. All fields – in particular electromagnetic fields – have fluctuations. In other words at any given moment their actual value varies around a constant, mean value. Even a perfect vacuum at absolute zero has fluctuating fields known as “vacuum fluctuations”, the mean energy of which corresponds to half the energy of a photon.
However, vacuum fluctuations are not some abstraction of a physicist’s mind. They have observable consequences that can be directly visualized in experiments on a microscopic scale. For example, an atom in an excited state will not remain there infinitely long, but will return to its ground state by spontaneously emitting a photon. This phenomenon is a consequence of vacuum fluctuations. Imagine trying to hold a pencil upright on the end of your finger. It will stay there if your hand is perfectly stable and nothing perturbs the equilibrium. But the slightest perturbation will make the pencil fall into a more stable equilibrium position. Similarly, vacuum fluctuations cause an excited atom to fall into its ground state.
The Casimir force is the most famous mechanical effect of vacuum fluctuations. Consider the gap between two plane mirrors as a cavity (figure 1). All electromagnetic fields have a characteristic “spectrum” containing many different frequencies. In a free vacuum all of the frequencies are of equal importance. But inside a cavity, where the field is reflected back and forth between the mirrors, the situation is different. The field is amplified if integer multiples of half a wavelength can fit exactly inside the cavity. This wavelength corresponds to a “cavity resonance”. At other wavelengths, in contrast, the field is suppressed. Vacuum fluctuations are suppressed or enhanced depending on whether their frequency corresponds to a cavity resonance or not.
An important physical quantity when discussing the Casimir force is the “field radiation pressure”. Every field – even the vacuum field – carries energy. As all electromagnetic fields can propagate in space they also exert pressure on surfaces, just as a flowing river pushes on a floodgate. This radiation pressure increases with the energy – and hence the frequency – of the electromagnetic field. At a cavity-resonance frequency the radiation pressure inside the cavity is stronger than outside and the mirrors are therefore pushed apart. Out of resonance, in contrast, the radiation pressure inside the cavity is smaller than outside and the mirrors are drawn towards each other.
It turns out that, on balance, the attractive components have a slightly stronger impact than the repulsive ones. For two perfect, plane, parallel mirrors the Casimir force is therefore attractive and the mirrors are pulled together. The force, F, is proportional to the cross-sectional area, A, of the mirrors and increases 16-fold every time the distance, d, between the mirrors is halved: F ~ A/d4. Apart from these geometrical quantities the force depends only on fundamental values – Planck’s constant and the speed of light.
While the Casimir force is too small to be observed for mirrors that are several metres apart, it can be measured if the mirrors are within microns of each other. For example, two mirrors with an area of 1 cm2 separated by a distance of 1 µm have an attractive Casimir force of about 10-7 N – roughly the weight of a water droplet that is half a millimetre in diameter. Although this force might appear small, at distances below a micrometre the Casimir force becomes the strongest force between two neutral objects. Indeed at separations of 10 nm – about a hundred times the typical size of an atom – the Casimir effect produces the equivalent of 1 atmosphere of pressure.
Although we do not deal directly with such small distances in our everyday lives, they are important in nanoscale structures and microelectromechanical systems (MEMS). These are “intelligent” micron-sized devices in which mechanical elements and moving parts, such as tiny sensors and actuators, are carved into a silicon substrate. Electronic components are then wired on to the device to process information that it senses or to drive the movement of its mechanical parts. MEMS have many possible applications in science and engineering, and are already used as car air-bag pressure sensors.
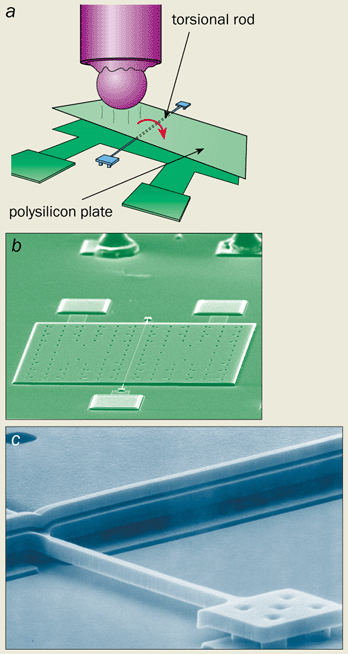
As MEMS devices are fabricated on the micron and submicron scale, the Casimir force can cause the tiny elements in a device to stick together – as reported recently by Michael Roukes and co-workers at the California Institute of Technology (2001 Phys. Rev. B 63 033402). But the Casimir force can also be put to good use. Last year Federico Capasso and his group at Lucent Technologies showed how the force can be used to control the mechanical motion of a MEMS device (2001 Science 291 1941). The researchers suspended a polysilicon plate from a torsional rod – a twisting horizontal bar just a few microns in diameter (figure 2). When they brought a metallized sphere close up to the plate, the attractive Casimir force between the two objects made the plate rotate. They also studied the dynamical behaviour of the MEMS device by making the plate oscillate. The Casimir force reduced the rate of oscillation and led to nonlinear phenomena, such as hysteresis and bistability in the frequency response of the oscillator. According to the team, the system’s behaviour agreed well with theoretical calculations.
Measuring the Casimir effect
When the Casimir effect was first predicted in 1948 it was very difficult to measure using the equipment of the time. One of the first experiments was carried out in 1958 by Marcus Spaarnay at Philips in Eindhoven, who investigated the Casimir force between two flat, metallic mirrors made from either aluminium, chromium or steel. Spaarnay measured the force using a spring balance, the extension of which was determined by the capacitance of the two plates. To prevent the Casimir force from being swamped by the electrostatic force, the mirrors had to be kept neutral by first touching them together before each measurement was made. Spaarnay also had to ensure that the plane mirrors were exactly parallel to each other, as the Casimir force is very sensitive to changes in distance. Spaarnay managed to overcome these difficulties and concluded that his results “did not contradict Casimir’s theoretical prediction”.
Since those early days, however, sophisticated equipment has made it much easier to study the Casimir effect. A new generation of measurements began in 1997. Steve Lamoreaux, who was then at the University of Washington in Seattle, measured the Casimir force between a 4 cm diameter spherical lens and an optical quartz plate about 2.5 cm across, both of which were coated with copper and gold. The lens and plate were connected to a torsion pendulum – a twisting horizontal bar suspended by a tungsten wire – placed in a cylindrical vessel under vacuum. When Lamoreaux brought the lens and plate together to within several microns of each other, the Casimir force pulled the two objects together and caused the pendulum to twist. He found that his experimental measurements agreed with theory to an accuracy of 5%.
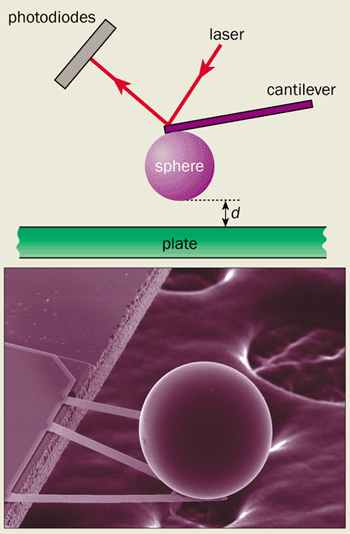
Inspired by Lamoreaux’s breakthrough, many other researchers tried new Casimir measurements. Umar Mohideen and co-workers at the University of California at Riverside, for example, attached a polystyrene sphere 200 µm in diameter to the tip of atomic force microscope (figure 3). In a series of experiments they brought the sphere, which was coated with either aluminium or gold, to within 0.1 µm of a flat disk, which was also coated with these metals. The resulting attraction between the sphere and the disk was monitored by the deviation of a laser beam. The researchers were able to measure the Casimir force to within 1% of the expected theoretical value.
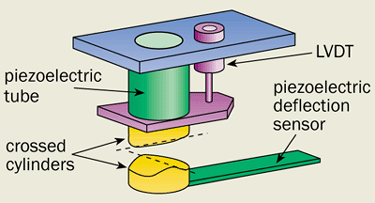
Thomas Ederth at the Royal Institute of Technology in Stockholm, Sweden, has also used an atomic force microscope to study the Casimir effect. He measured the force between two gold-coated cylinders that were arranged at 90° to each other and that were as little as 20 nm apart. His results agreed to within 1% of theory (figure 4).
However, very few recent experiments have measured the Casimir force using the original configuration of two plane, parallel mirrors. The reason is that the mirrors have to be kept perfectly parallel during the experiment, which is difficult. It is much easier to bring a sphere close up to a mirror because the separation between the two objects is simply the distance of closest approach. The only drawback of using a sphere and a plane mirror is that the calculations of the Casimir force are not as accurate as those between two plane mirrors. In particular it has to be assumed that the contributions to the force between the sphere and plate are completely independent at each point. This is true only if the radius of the sphere is much larger than the distance between it and the plate.
The only recent experiment to replicate Casimir’s original set-up of two plane, parallel mirrors was carried out by Gianni Carugno, Roberto Onofrio and co-workers at the University of Padova in Italy. They measured the force between a rigid chromium-coated plate and the flat surface of a cantilever made from the same material that were separated by distances ranging from 0.5-3 µm (G Bressi et al. 2002 Phys. Rev. Lett. 88 041804). The researchers found that the measured Casimir force agreed to within 15% of the expected theoretical value. This relatively poor fit reflected the technical difficulties involved in the experiment.
Improved calculations
The problem with studying the Casimir effect is that real mirrors are not like the perfectly smooth plane mirrors that Hendrik Casimir originally considered. In particular, real mirrors do not reflect all frequencies perfectly. They reflect some frequencies well – or even nearly perfectly – while others are reflected badly. In addition, all mirrors become transparent at very high frequencies. When calculating the Casimir force the frequency-dependent reflection coefficients of the mirrors have to be taken into account – a problem first tackled by Evgeny Lifshitz in the mid-1950s, and then by Julian Schwinger and many others.
It turns out that the measured Casimir force between real metallic mirrors that are 0.1 µm apart is only half the theoretical value predicted for perfect mirrors. If this discrepancy is not taken into account when comparing experimental data with theory, then an experimental measurement could erroneously be interpreted as a new force. My colleague Serge Reynaud and I have taken into account the real behaviour of mirrors in our calculations using the physical properties of the metals themselves. We found that the simple solid-state models of the mirror match the real behaviour only above 0.5 µm.
Another problem with calculating the expected Casimir force for a real system is the fact that experiments are never carried out at absolute zero – as originally envisaged in Casimir’s calculations – but at room temperature. This causes thermal – as well as vacuum – fluctuations to come into play. These thermal fluctuations can produce their own radiation pressure and create a bigger Casimir force than expected. For example, the Casimir force between two plane mirrors 7 µm apart is twice as large at room temperature than at absolute zero. Fortunately, thermal fluctuations at room temperature are only important at distances above 1 µm, below which the wavelength of the fluctuations is too big to fit inside the cavity.
Although the temperature dependence of the Casimir force has not yet been studied in detail experimentally, it must be included in calculations of the force at separations above 1 µm. Many researchers have tackled this problem for perfectly reflecting mirrors, including Lifshitz and Schwinger back in the 1950s. It has also been examined more recently by Michael Bordag at Leipzig University, Bo Sernelius at Linköping University in Sweden, Galina Klimchitskaya and Vladimir Mostepanenko at the University of Paraiba in Brazil, and by our group in Paris. Indeed the temperature dependence of the Casimir force was for some time a matter of hot debate in the community. The various contradictions, however, now seem to have been resolved, and this has given an additional motivation to an experimental observation of the influence of temperature on the Casimir force.
A third and final problem in calculating the Casimir force is that real mirrors are not perfectly smooth. Most mirrors are made by coating a substrate with a thin metal film using the technique of “sputtering”. However, this produces films with a roughness of about 50 nm. While such roughness is invisible to the naked eye, it does affect measurements of the Casimir force, which is very sensitive to small changes in distance.
Mohideen and his group in California have recently used surface deformations to show that two surfaces can also have a lateral Casimir force that acts in a parallel – rather than a perpendicular – direction to the surface of the mirrors. In the experiments they prepared specially corrugated mirrors the surfaces of which were sinusoidally curved. They then moved the mirrors parallel to one another so that a peak of one mirror passed successively over the peaks and troughs of the other mirror. The researchers found that the lateral Casimir force varied sinusoidally with the phase difference between the two corrugations. The size of the force was about ten times smaller than the ordinary Casimir force between two mirrors the same distance apart. The lateral force is also due to vacuum fluctuations.
Mehran Kadar and co-workers at the Massachusetts Institute of Technology have calculated a theoretical value for the force between two perfectly reflecting corrugated mirrors, while Mohideen and colleagues evaluated the lateral force for metallic mirrors and found good agreement with experiment. The lateral Casimir force may have yet another consequence for micromachines.
New physics?
The Casimir effect could also play a role in accurate force measurements between the nanometre and micrometre scales. Newton’s inverse-square law of gravitation has been tested many times at macroscopic distances by observing the motion of planets. But no-one has so far managed to verify the law at micron length scales with any great precision. Such tests are important because many theoretical models that attempt to unify the four fundamental forces of nature predict the existence of previously undiscovered forces that would act at such scales. Any deviation between experiment and theory could hint at the existence of new forces. But all is not lost even if both values agree: the measurements would then put new limits on existing theories.
Jens Gundlach and colleagues at Washington, for example, have used a torsion pendulum to determine the gravitational force between two test masses separated by distances from 10 mm down to 220 µm. Their measurements confirmed that Newtonian gravitation operates in this regime but that the Casimir force dominates at shorter distances. Meanwhile Joshua Long, John Price and colleagues at the University of Colorado – together with Ephraim Fischbach and co-workers from Purdue University – are trying to eliminate the Casimir effect altogether from sub-millimetre tests of gravitation by carefully selecting the materials used in the experiment.
This article only gives a flavour of the many experimental and theoretical studies of the Casimir effect. There are many other exciting developments as well. Many groups are, for example, looking at what would happen if the interaction between two mirrors is mediated not by an electromagnetic field – which is made up of massless bosons – but by fields made of massive fermions, such as quarks or neutrinos. Other research teams, meanwhile, are studying the Casimir effect with different topologies, such as Möbius strips and doughnut-shaped objects.
But despite the intensive efforts of researchers in the field, many unsolved problems about the Casimir effect remain. In particular the seemingly innocent question of the Casimir force within a single hollow sphere is still a matter of lively debate. People are not even sure if the force is attractive or repulsive. Hendrik Casimir himself thought about this problem as early as 1953 while looking for a stable model for the electron. Half a century on, the mysteries of the Casimir force are likely to keep us entertained for many years to come.