The idea that the universe is trapped on a membrane in some high-dimensional space–time may explain why gravity is so weak, and could be tested at high-energy particle accelerators.

is stimulating both physicists and artists. (Courtesy: Richard Deacon)
The possibility of extra dimensions, beyond the three dimensions of space of our everyday experience, sometimes crops up as a convenient, if rather vague, plot in science fiction. In science, however, the idea of extra dimensions has a rich history, dating back at least as far as the 1920s. Recently there has been a remarkable renaissance in this area due to the work of a number of theoretical physicists. It now seems possible that we, the Earth and, indeed, the entire visible universe are stuck on a membrane in a higher-dimensional space, like dust particles that are trapped on a soap bubble.
In this article we look at the major issues behind this new development. Why, for example, don’t we see these extra dimensions? If they exist, how can we detect them? And perhaps the trickiest question of all: how did this fanciful idea come to be considered in the first place?
A long-standing idea
The whole notion of extra dimensions has its origin in the search for a unified theory of the forces observed in nature. The story began in the 1860s with the unification of the electric and magnetic forces by James Clerk Maxwell. As well as the extraordinary prediction that light is an electromagnetic wave, Maxwell’s theory had a hidden property that was not realized until much later. It has what we now call a “gauge symmetry”.
Gauge symmetry can be visualized in the following geometrical way. Suppose that every charged particle has associated with it an arrow that can rotate round in a circle like one of the hands of a clock. This rotation does not take place in the 3-D space that we observe, so the circle is – for the moment – purely mathematical, and the symmetry, known as U(1), is deemed “internal”. The symmetry principle states that the absolute positions of these arrows can never be determined. Moreover, the symmetry is said to be “gauged” or “local” – meaning that the definition of absolute arrow position can change with time and location. Allowing such variations introduces a spurious current unless we add an extra ingredient to exactly compensate for it. This extra mathematical ingredient is the electromagnetic field.
The presence of this field explains the physical properties we associate with electromagnetism. For example, the field carries pulses of energy that we observe as particles of light – photons – and the exchange of photons results in the net electromagnetic force between charged particles.
In the 1920s Maxwell’s unification of electricity and magnetism, together with Einstein’s new general theory of relativity, inspired Theodor Kaluza and Oskar Klein to suggest that it might be possible to unify electromagnetism and gravity in an overarching geometrical scheme involving extra dimensions.
General relativity is a wonderful example of a geometrical theory. It too is derived from a local symmetry, known as Lorentz symmetry, that involves the four dimensions (three space plus one time) of everyday experience. In this case, velocities are like the arrows of the U(1) symmetry. So Lorentz symmetry incorporates the fact that the results from physical experiments are independent of the direction from which we view them and of our velocity. General relativity makes the symmetry local and, as for electromagnetism, that requires a field – which in this case is the geometry of space-time itself. Local “ripples” in space-time are the gravitational equivalent of photons – gravitons.
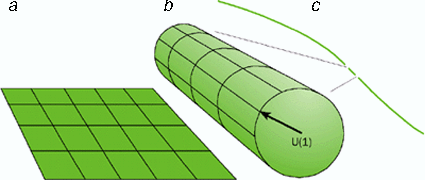
Inspired by this idea, Kaluza and Klein proposed including the U(1) symmetry of electromagnetism into this geometric scheme by adding a fourth spatial dimension, giving a total of five. The 5-D space-time begins with the full 5-D Lorentz symmetry. However, if the extra dimension is curled up on itself, or “compactified”, part of the symmetry is lost. What remains is precisely the 4-D Lorentz symmetry of general relativity and the U(1) gauge symmetry of electromagnetism. In this picture, the “internal space” of electromagnetism is actually a real extra dimension that is curled up, and the photon is really a component of the higher-dimensional graviton (see figure 1).
The Kaluza-Klein theory was a beautiful and audacious idea, and today seems remarkably prescient. Indeed, our modern geometric picture of gauge theories makes it seem almost natural. However, the Kaluza-Klein theory suffered from a number of serious faults. First, it failed to explain why the strength of the electromagnetic force is quite large while the gravitational force is fantastically weak. Second, quantum mechanics, which was developing rapidly at the time of Kaluza and Klein, could be incorporated into the theory of electromagnetism rather neatly, but not into the theory of gravity. Quantum gravity seemed to be plagued by infinities, which rendered calculations of physical processes useless. Finally, two more forces – the weak and strong forces – were discovered, and these did not seem to fit easily into the Kaluza-Klein picture.
Superstring theory: dimensions galore
Given some artistic licence, it is probably fair to say that interest in extra dimensions waned until the advent of supersymmetry and string theory in the 1970s and 1980s. Supersymmetry is a theory that relates the two different kinds of particles allowed by quantum mechanics – fermions and bosons. Fermions are particles that have half-integer values of intrinsic angular momentum or “spin”, and include all the known particles of matter, such as electrons and protons. Meanwhile, bosons are particles with integer values of spin, including photons and gravitons.
Supersymmetry has a number of remarkable properties. In particular, it removes some of the infinities of quantum gravity. Moreover, the most symmetric forms of supersymmetry are naturally formulated in 10 or 11 dimensions.
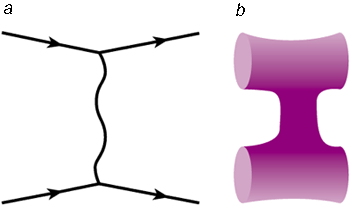
String theories were a curiosity that had been around since the early 1970s. In these theories, the world is described by the interactions of 1-D objects called strings, rather than by the interaction of particles (figure 2). In string theory, the different “particles” can be thought of as different modes of vibration of the string. Moreover, there is one mode that has the properties of the graviton, which means that gravity is automatically included in the theory.
In the mid 1980s Michael Green, then at Queen Mary College in London, and John Schwarz of the California Institute of Technology, and others made a fortunate discovery. They realized that when supersymmetry and string theory are combined, the resulting “superstring” theory rather successfully incorporates quantum mechanics without the troublesome infinities, provided there are 10 space-time dimensions. So here, at last, was a candidate theory of quantum gravity – as long as we could accept that our apparently 4-D world has an extra six dimensions that are very tightly rolled up or compactified as in the old Kaluza-Klein idea.
Shortly after this breakthrough, a certain type of superstring theory – known as “heterotic” – became the focus of attention, since it possessed a gauge symmetry that was large enough to include all the known forces in a unified way.
These marvellous properties led to an explosion of interest. However, in a sense, string theory was a victim of its own theoretical success. There were simply far too many consistent solutions to the equations of string theory. Many of these solutions resembled our world, but many more did not. Worse, there was no dynamical mechanism that preferred one solution to any of the others, so string theory provided no explanation of the detailed properties of our world. It even failed to explain why the universe has three large space dimensions and not nine or ten. This problem, which is still with us today despite considerable progress, is called the “degeneracy problem”.
There was another feature of heterotic string theories that was discouraging. General arguments suggested that it would probably never be possible to test string theory directly. These arguments involve dimensional analysis. For example, what is the typical size of a string – the so-called string length? Since string theory is a theory of quantum gravity, we can construct a unit of length lPlanck = (GNh-bar/c3)1/2, where GN is Newton’s constant, h-bar is the Planck constant divided by 2 pi and c is the speed of light. Because gravity is such a weak force, this length turns out to be an extraordinarily small number, some 10-35 m – about 1019 times smaller than an atomic nucleus. The energy we would need to probe such a small size is described in terms of the equivalent mass, known as the Planck mass. At 1.2 x 1019 GeV c-2, the Planck mass is a dismayingly large number.
The huge Planck mass means that if such a string theory provides the correct description of quantum gravity, then everything we see today is essentially massless as far as the theory is concerned. String-theory effects would only show up if particle accelerators could reach Planck energies and “pluck” some of the higher modes of the string. Such high energies are some 1016 times higher than those that can be achieved at current particle accelerators and are almost certainly beyond our capabilities.
However, there are loopholes in these general arguments, which models constructed independently by Ignatios Antoniadis, then at the Ecole Polytechnique in Paris, and Joe Lykken of Fermilab in the US tried to exploit in the early 1990s. In estimating the string length and the Planck mass, many theorists assumed that all the dimensionless parameters of the theory were of order one. In particular, this assumption led to the prediction that the typical size of the compactified extra dimensions is the same as the typical string scale.
However, Antoniadis and Lykken argued that the theory can dynamically generate very large or very small numbers as a consequence of the degeneracy problem. As a result, the size of the compactified extra dimensions could be much larger. And if they were large enough, string-theory effects would become visible at accessible energies.
Unfortunately, these early models of Antoniadis and Lykken had severe difficulty incorporating the three well-measured gauge forces – electromagnetism, the weak and the strong force – in a successful way. But they were important and interesting precursors to the more recent remarkable developments.
The world as a brane
Up to this point, people had assumed that gravity – together with the electromagnetic, strong and weak gauge forces – lives everywhere in 10-D space-time. However, a new possibility was brought to light in 1998 by Nima Arkani-Hamed at the Stanford Linear Accelerator Center in California, Savas Dimopoulos of Stanford University and Gia Dvali of the International Centre for Theoretical Physics in Trieste, Italy. They asked a rather general question: could gravity be the only force that is aware of extra dimensions? And if so, how large could the extra dimensions be?
If this were the case, the world would look as shown in figure 3. The electromagnetic, weak and strong forces, as well as all the matter in the universe, would be trapped on a surface with three spatial dimensions, like dust particles on soap bubbles. Only gravitons would be able to leave the surface and move throughout the full volume. This 3-D surface is known as a “brane”, a name derived from membrane, the 2-D equivalent.
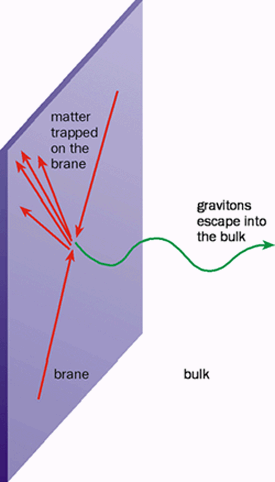
If the strong, electromagnetic and weak gauge forces are trapped on a brane, the answer to how large the “gravity-only” extra dimensions could be is surprising. Since we do not see extra dimensions in everyday life, we naturally assume that they must be tiny. However, our everyday experiences are prejudiced by electromagnetism, which is trapped on the brane. Meanwhile, the highest energy particle accelerators extend our range of sight to include the weak and strong forces down to small scales, around 10-15 mm. We may therefore be blissfully unaware of any extra dimensions.
The only force we can use to probe gravity-only extra dimensions is, of course, gravity itself. Remarkably we have almost no knowledge of gravity at distances less than about a millimetre. This is because the direct tests of the gravitational force are based on torsion-balance experiments that measure the attraction between oscillating spheres (see Long et al. in further reading). The smallest scale on which this type of tabletop experiment has so far been performed is 0.2 mm.
Hence, below about 1 mm, objects could be gravitating in five or more dimensions. However, we know that the strong, weak and electromagnetic forces cannot be modified at distances larger than about 10-15 mm. This prompted Arkani-Hamed, Dimopoulos and Dvali to suggest that these forces might be trapped on a brane that has three spatial dimensions large enough to incorporate the entire visible universe, yet a “thickness” of at most 10-15 mm in the extra-dimensional world.
Let’s look in more detail at how forces behave in a brane world with a single extra dimension of size L. The electromagnetic, weak and strong forces, trapped within the 3-D brane, are not aware of the extra dimension and so maintain their usual behaviour. Gravity, on the other hand, behaves rather differently. If we approach a massive body closer than a distance L, we would feel the effects of a force law in four spatial dimensions rather than three. In this case, the gravitons from the massive body are spread over a 4-D sphere with radius r, the surface area of which grows as r3. We would then find that the gravitational force follows a 1/r3 law.
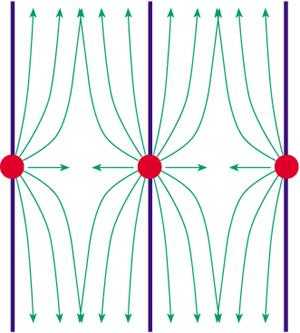
However, as we move further away from the body (i.e. r > L) the usual 1/r2 behaviour is restored. The reason for this is as follows. Adding a compactified extra dimension is rather like standing between two mirrors; we see images of ourselves stretching to infinity. In the Arkani-Hamed-Dimopoulos-Dvali picture the same is true, except the images of the original brane are spaced every L apart and are only “seen” by the gravitational force (see figure 4).
Now consider the gravitational force coming from a massive body trapped in the brane. If we are much further away than L, then we are gravitationally attracted by the original body plus all its mirror images. When we are at a distance r > L along the brane from the original body, the gravitons from it and its infinite line of mirror images are spread out evenly over a 4-D “cylinder” of radius r, and the gravitational force follows the usual 1/r2 behaviour. However, as a result of the initial higher-dimensional spreading, the force of gravity is much weaker than it would otherwise be.
In other words, the only reason the gravitational force appears to be so weak could be because it is diluted by the extra dimensions. This aspect of the world-as-a-brane scenario particularly interested Arkani-Hamed, Dimopoulos and Dvali precisely because it reformulated the question of why gravity is so much weaker than the other forces (or equivalently, why the Planck energy of 1019 GeV is so much larger than the energy scale of weak interactions, around 1000 GeV).
In this picture, Newton’s constant is a derived quantity that depends on the volume of the extra dimensions. When viewed from the higher-dimensional space, known as the “bulk”, there might be only one fundamental scale. The most radical suggestion lowers the fundamental scale of gravity to the weak energy scale, about 1000 GeV. This assumption leads to an estimate for the size of the extra dimensions in terms of their number, with higher numbers of extra dimensions implying smaller compactification scales.
If there is only one extra dimension then it turns out that it must be larger than the solar system and this possibility can be safely excluded. Two extra dimensions, on the other hand, give a compactification scale of roughly 1 mm, which is close to the current experimental limit. This experimental possibility is one of the most exciting aspects of the world-as-a-brane picture. Suddenly, from believing that a theory of quantum gravity would for ever be beyond the reach of experiments, it seemed as if we might be able to test the theory in tabletop experiments. Such experiments might show the usual Newtonian 1/r2 force law switch to a 1/r4 law, which would characterize two extra dimensions.
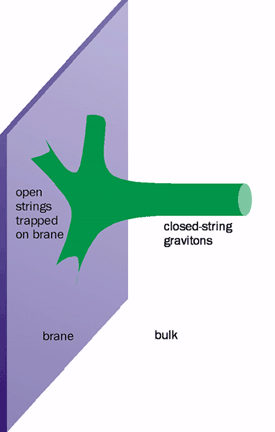
The theoretical constructs necessary for the brane-world picture mirrored the developments that had been independently taking place in string theory. One aspect of these developments was the mathematical discovery that extended objects of various dimensionalities are integral to string theory. There turned out to be many well defined examples of such objects, generically called p-branes, where p is the number of spatial dimensions of the object. For example, a 0-brane is similar to a normal point-like particle, a 1-brane is like a string, a 2-brane resembles a membrane, and so on.
Intense interest was stimulated in p-branes following work in 1995 by Joe Polchinski of the University of California at Santa Barbara among others. String-theory p-branes are good candidates for brane worlds because they possess gauge symmetries on their “surfaces” and automatically incorporate a quantum theory of gravity, namely string theory. The gauge symmetry arises from “open” strings, strings that have their endpoints stuck on the brane. Meanwhile, two of these open strings can collide to form a loop of closed string that can travel into the higher-dimensional bulk (figure 5). The simplest excitation modes of these closed strings correspond precisely to gravitons.



