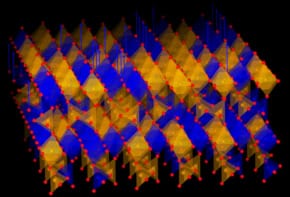
Linkages are fundamental components to machines with moving parts. The term describes any assembly of rigid bodies connected by joints. From this vast catalogue of structures, the linkages that most often interest engineers are those with just one internal degree of freedom, meaning they can only change shape in one way, which allows greater mobility control.
Until recently only a few linkages met this requirement – scissorlike elements, the Sarrus linkage, the Bennett linkage, and the Bricard linkage. Now researchers at Okinawa Institute of Science and Technology in Japan have unearthed a whole new class of ring linkages with just one internal degree of freedom – Möbius Kaleidocycles. Reporting in the Proceedings of the National Academy of Sciences, they suggest that technological applications of their discovery may include robotics and “the design of new organic ring molecules with peculiar electronic properties”, as well as raising fundamental questions about geometry, topology, and the limitations of mobility for closed loop linkages.
A degree of freedom
The researchers – Johannes Schönke and Eliot Fried – began by examining the classic sixfold conventional kaleidocycle described by six tetrahedra joined by orthogonal hinges at opposing edges to form a closed ring. The only internal degree of freedom of these structures is an everting motion where different faces of the tetrahedra are exposed as the structure is continuously turned inside out. In contrast for example an eightfold kaleidocycle has two internal degrees of freedom, pressing Schönke and Fried to enquire “How many degrees of freedom does a ring of N tetrahedra linked by N revolute hinges generally have?”
To tackle this the researchers devise a definition for the degrees of freedom of the corners of the kaleidocycle tetrahedra as constrained by the tetrahedron edges. However after subtracting the external six degrees of freedom corresponding to translations and rotations of a rigid body in space, their definition leads to a sixfold kaleidocycle with no internal degrees of freedom.
“It transpires that a K6 [sixfold kaleidocycle] is a nontrivial example of an overconstrained mechanism,” explain Schönke and Fried in their report. “Its high symmetry allows for a hidden degree of freedom.”
A twist in the tale
Next the researchers expanded their investigation to kaleidocycles of conjoined tetrahedra with a twist so that the formally orthogonal hinged edges are no longer at right angles. They found that for kaleidocycles of seven or more tetrahedra there is a critical angle below which it is no longer possible to form a closed loop.
In addition, at the critical angle, all internal degrees of freedom collapse leaving just one as in the case of the classical sixfold kaleidocycle. Since the rings formed in this way share the topology of a Möbius band – recently familiar as the recycle icon – the researchers describe them as Möbius kaleidocycles.
Origami brings soft logic to robotics
Analogous annulene chemistry
Robotics is one of the fields most likely to benefit from this new class of kaleidocycles with their incorporation in robotic arms or self-propelling swimming rings. However, Schönke and Fried also highlight possibilities to explore in organic chemistry.
They highlight previous work on Möbius annulenes, monocyclic hydrocarbon compounds like benzene but with the twisted Möbius topology. In the 1920s Edgar Heilbronner showed that Möbius annulenes should have novel electronic properties. In 2014 Gaston Schaller at the University of Kiel in Germany and colleagues synthesised an annulene with a threefold Möbius band topology that was energetically favourable over its former onefold counterpart. Drawing an analogy between the “twist into writhe” strategy Schaller and colleagues use to produce an annulene with a lower strain, and the minimum critical twist angle of the topologically equivalent Möbius Kaleidocycles, Schönke and Fried conclude, “We hypothesize that an annulene made from molecular building blocks (equivalent to our tetrahedra) with a twist angle close to the critical angle should exhibit minimal strain.”
Future topics for further fundamental investigations include the possibility of other ring linkages with more than seven elements and only one degree of freedom, an explanation for the everting motion that the ring geometries can undergo, and other possible topologies and geometries.
Full details are reported in the Proceedings of the National Academy of Science.