Despite its many useful properties, a particular feature of the “wonder material” graphene, namely the emergent “valley Hall effect”, has been puzzling researchers for a decade, as condensed-matter physicists Luis Foà Torres and Sergio O Valenzuela explain
Since it was first successfully isolated in 2004, the “wonder material” graphene, with its honeycomb-like 2D structure and its wide gamut of interesting properties, has been keenly studied by material scientists. In recent years, however, the focus has shifted from simply exploring its physical properties to using graphene as a platform for testing and realizing a plethora of novel ideas. This was especially apparent with the “From graphene physics to graphene for physics” theme of the 2017 Solvay workshop on graphene. And, like a relentless spring of fresh water from different sources, graphene is still unveiling surprises.
Today, there are numerous areas of research in the field where lively discussions are being had. Superconductivity in rotated graphene layers, for example, is of interest to many researchers, as it may open the door to a better understanding of superconductivity as a whole. But a key puzzle in graphene is the material’s perplexing non-local response, which has seeded a series of studies addressing the use of graphene’s “valley degree of freedom”.
Electrons have fundamental properties – such as “charge” and “spin” – which allow for a number of emergent phenomena such as magnetism. Certain semiconductors and 2D materials possess a similar property known as the “valley” degree of freedom. In these materials, the states at the Fermi surface are distributed in pockets, in the crystal momentum space. Each of these pockets is called a valley, which corresponds to a specific electronic state. Graphene is a zero-gap semiconductor with two valleys (usually called K and K’); its conduction and valence bands meet at discrete points, known as Dirac points.
In the valley
Just as “spintronics” – which makes use of the internal degree of freedom of spin to store and manipulate bits of information – this valley degree of freedom is at the centre of a stream of research aiming to exploit it for “valleytronics”, where the information would be stored as discrete values of the crystal momentum. One of the challenges in this field is that transport measurements sense charge not valley, making it difficult to detect valley currents. Furthermore, a high crystalline quality of graphene is required, as atomic defects would normally produce intervalley scattering.
However, in 2007 Di Xiao and colleagues, then at the University of Texas, Austin, found that if inversion symmetry is broken and an electric field driving a current is present, then the charge carriers would bend their trajectories, as in the presence of a magnetic field. Their direction of travel is then determined not by the sign of their charge, but by their valley (Phys. Rev. Lett. 99 236809). Essentially, graphene can be coaxed into exhibiting a “valley Hall effect” – similar to the spin Hall effect – by creating an asymmetry between the two valleys, such that electrons move across the sample in opposite directions when a current is run across it.
A puzzling non-local response
In 2014, nearly a decade after the isolation of graphene in electrical devices, condensed-matter physicist Roman Gorbachev at the University of Manchester, UK, and collaborators including graphene Nobel laureates Andre Geim and Konstantin Novoselov, characterized multi-terminal graphene samples, by looking for topological currents in graphene superlattices (Science 346 448). Inspired by experiments on quantum and spin Hall systems, their experiment was designed to probe the non-local response, and led to the observation of a remarkable effect that has puzzled scientists ever since.
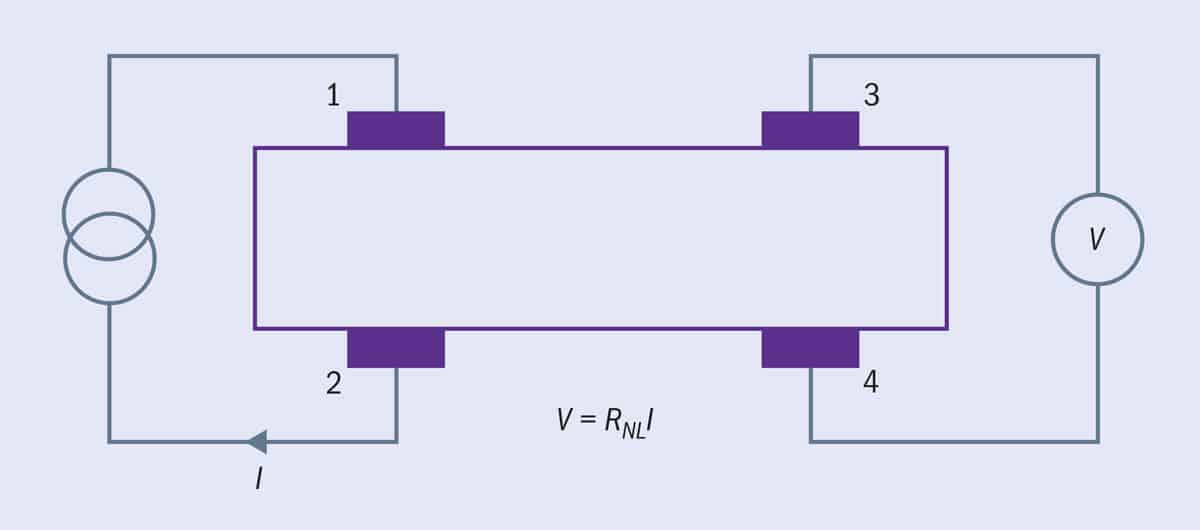
In Gorbachev’s measurements a current, I, is applied between two terminals while the voltage, V, is measured far (several microns) away, between two different terminals (figure 1), where no current flows and an ohmic contribution is not expected. In these experiments graphene was placed on a special substrate of hexagonal boron nitride (hBN), which, when carefully aligned, breaks the graphene lattice inversion symmetry. Furthermore, the Fermi level could be tuned thanks to a back-gate voltage. The team’s findings showed sharp peaks in the non-local resistance V/I versus back-gate voltage, only when inversion symmetry was broken. The peaks appeared near Dirac points in the absence of a magnetic field and implied that a voltage developed microns away from the current probes.
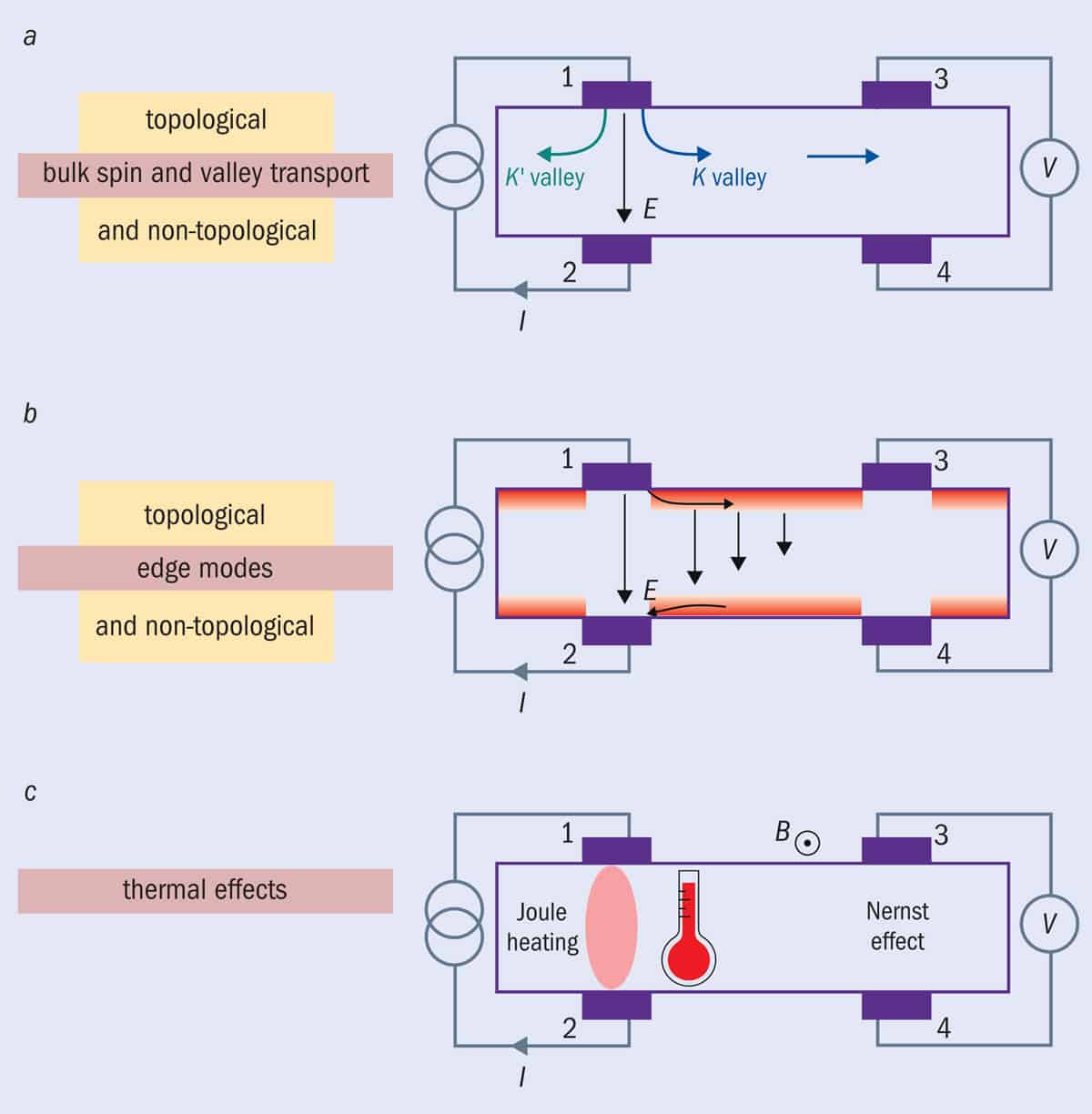
To rationalize these unusual findings, Gorbachev and colleagues relied on the valley Hall effect, which they connected to the non-local response. More details on the theory were published almost a year later (PNAS 112 10879) by Justin Song at the California Institute of Technology, and colleagues. The researchers modelled a system made of graphene stacked atop hBN, and wrote that the “Berry curvature manifests itself in transport via the valley Hall effect and long-range chargeless valley currents. The non-local electrical response mediated by such currents provides diagnostics for band topology.” The experiments were then explained in terms of such charge-less valley currents flowing far away close to the voltage probes (figure 2a).
Strikingly, and unlike other cases where topological effects are tied to robust states at the edges (through a bulk-boundary correspondence), the charge-less valley currents predicted by Xiao’s research are not due to states appearing at the boundary but rather states in the Fermi sea beneath the gap, and are signalled to have a consequence in the non-local response.
Further findings, and seeds for a controversy
The story continues with a number of subsequent experiments (Nature Phys. 11 1027; Nature Phys. 11 1032; Appl. Phys. Lett. 114 243105), all of which looked at topological valley currents, and confirm the observation of a large anomalous non-local resistance. This time, the experiments were not carried out on graphene stacked on hBN. Instead, they looked at bilayer graphene, where the strength of the inversion symmetry breaking term could be tuned by means of a perpendicular electric field. Other related experiments attempted to map the current flow leading to the non-local signal (Nature Comms 8 14552), and even explored a ballistic version of these phenomena (Comms Phys. 3 224).
But at the same time, a 2015 paper by theorist George Kirczenow of the Simon Fraser University in Canada triggered a debate on the interpretation of the results (Phys. Rev. B 92 125425). By using scattering theory, Kirczenow pointed out that the non-local resistance peaks cannot be taken as a signature of the anomalous velocities produced by an electric field and the non-vanishing Berry curvature. A crucial point leading to this conclusion was the fact that the use of a semiclassical theory is unclear because, in the experiments by Gorbachev and colleagues, the Fermi level is tuned within an electronic gap.
Kirczenow argued that a more suitable approach is provided by the Landauer–Büttiker theory – one of the most widely used quantum-transport theories, where voltage and current sources appear on equal footing. Current flow is expressed in terms of transmission probabilities, whereas in other views (including the semiclassical one) it is seen as the response to an external field. All quantities can then be computed from the scattering matrix obtained for a Hamiltonian in absence of the electric field, thus depriving the non-local resistance of the crucial ingredient associated with the anomalous velocity.
Fermi sea versus surface
Considering the disparate views, the scene was set for a clash of interpretations and methodologies and many colleagues wondered whether we had hit a so-called “valley of death”. Indeed, a 2018 study by Juan Marmolejo-Tejada of Montana State University and colleagues aimed at deciphering the non-local resistance in graphene on hBN using an ab initio or “first principles” method of quantum transport. They showed that graphene with zigzag edges on hBN hosts dispersive edge states near the Dirac point (J. Phys. Mater. 1 015006). The team suggested that these peculiar edge states, absent in simplified descriptions, lead to non-local signals that can persist at long distances, while withstanding edge disorder. Marmolejo-Tejada and collaborators concluded that the non-local signals in earlier experiments may stem from edge states at the Fermi surface, rather than being a topological response from bulk states deep in the Fermi sea (figure 2b).
Earlier this year, Thomas Aktor from the Technical University of Denmark and collaborators brought a new twist to this debate by suggesting that the valley Hall effect can indeed enhance the non-local resistance (Phys. Rev. B 103 115406). However, they claim that the mechanism would arise not from Berry curvature effects inside a bulk gap, but from the non-uniform gap profile produced in graphene/hBN heterostructures by the Moiré (interference) pattern. The authors propose a way of engineering substrates and tailored defects (through controlled deposition of atomic clusters or drafted molecular patterns) to produce bulk-driven valley Hall effects.
Topological or non-topological response?
New experiments published this year, looking at the long-range non-topological edge currents in charge-neutral graphene, add even more surprising pieces to this puzzle (Nature 593 528). As in the original experiments by Gorbachev’s team, Amit Aharon-Steinberg at Weizmann Institute of Science in Israel and colleagues have implemented non-local transport measurements in hBN-encapsulated graphene at low temperatures. Their experiments, however, are carried out under moderate magnetic fields of up to 5 T; and they combine transport experiments with a superconducting interference device on a tip for thermal imaging and scanning gate microscopy.
When it comes to transport experiments, the observations largely reproduced previous investigations, in particular the unexpectedly large non-local resistance at zero magnetic field (figure 2c). This becomes orders of magnitude larger as the magnetic field is increased from 0 to 5 T, a phenomenon that was ascribed to spin and thermo-magnetoelectric effects by Gorbachev’s team in 2011 (Science 332 328). However, scanning thermal imaging in the same sample suggested that Joule heating and non-local resistance are highly correlated, even at zero magnetic field. Indeed, when a large non-local resistance develops, the temperature increase spreads across the sample, which casts doubt about the relevance of non-dissipative valley currents.

The temperature distribution and scanning gate microscopy measurements point towards predominant edge transport, driven by the presence of edge charge accumulation resulting from band bending, thereby ruling out the bulk mechanisms invoked in earlier works. As Aharon-Steinberg and colleagues remark in their paper, the edge currents are not protected by topology and are extremely sensitive to edge disorder. They coexist with the bulk conduction and their effect can be felt over long distances if the conductivity of the edge states is relatively large in comparison to the bulk.
Within the scenario they propose, the sharp peak non-local resistance at zero magnetic field would be largely trivial. In regions where the bulk carrier density is suppressed – either by tuning the Fermi level at a Dirac point in graphene or by opening a gap in bilayer graphene – edge transport is bound to become more relevant. However, although the mechanism relies on non-topological edge states just as suggested by Marmolejo-Tejada, there seem to be some pieces that are still missing.
Indeed, it is unclear whether the edge conductance found by Aharon-Steinberg is sufficient to explain the non-local response that Gorbachev observed, at zero magnetic field. In addition, the correlation between broken lattice symmetry discovered by the Manchester team, with the observation of large non-local resistance, remains inconclusive. Aharon-Steinberg’s results correspond to a single sample in which the alignment between graphene and hBN is not addressed.
More than one phenomenon
All of this leaves us with many questions and it is fair to wonder whether the non-local response in the samples Gorbachev and colleagues studied is actually due to crystal alignment, or simply some serendipity, explained by the occurrence of uncontrolled edge impurities and defects. However, this seems unlikely, given that so many samples were used in the study, thus suggesting that there may be more than one phenomenon at play. If there is a contribution to the non-local response at zero magnetic field originating from both edge and valley currents, when inversion symmetry is broken, it will be necessary to determine how important their relative contributions are and whether a unified framework can be used to describe them. This in itself seems difficult due to the clash of methodologies explained earlier.
The comparison between the results at zero and non-zero magnetic fields also requires further attention. Experiments have largely focused on one case or the other, and specific mechanisms have been invoked to explain them. When a magnetic field is applied, the observations have been ascribed to spin and thermo-magnetoelectric effects, or to edge states. However, these observations at varying magnetic field share many features and therefore could be manifestations of the same phenomenon – even though, currently, a combination of multiple phenomena cannot be ruled out.
For the moment, these observations call for a careful re-examination of some of the reported non-local transport phenomena
As Argentine author Julio Cortázar writes in his famous novel Hopscotch “I discover new worlds which are simultaneous and alien, and every time I get the feeling more and more that to agree is the worst of illusions.” In effect, contrasting viewpoints are the fuel that move science forward. For the moment, as Aharon-Steinberg writes, these observations call for a “careful re-examination of some of the reported non-local transport phenomena”. Further experiments may well provide us with more decisive clues. Whatever the outcome of this debate, it seems certain that a valley of opportunities still lies ahead.