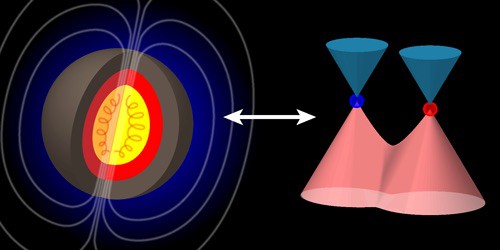
The astrophysical dynamo effect could be tested in the laboratory using electronic materials such as hydrodynamic Weyl metals. So says a team of physicists in the US who has determined the conditions under which the effect can appear in these topological materials by calculating the Reynolds number – an important figure of merit for the onset of turbulence in the electron liquid in a Weyl metal, which leads in turn to the dynamo effect. This number can be large enough to create a dynamo-induced magnetic field that might be detected in an experiment.
“The dynamo effect is a beautiful astrophysical phenomenon, first proposed by Larmor in 1919, that is believed to be responsible for generating and sustaining magnetic fields in galaxies, stars, and planets, including the Sun and Earth,” write Victor Galitski of the University of Maryland, Mehdi Kargarian, now at Sharif University in Tehran, and Sergey Syzranov of UC Santa Cruz. Although there are many different dynamo mechanisms, they all share the same key ingredient, they say: the turbulent motion of viscous, electrically conducting gases and plasmas over large length scales.
Recreating the dynamo effect in lab experiments
To better understand this theory, researchers have been trying to recreate smaller versions of the dynamo effect in lab experiments. These are challenging to set up to say the least since they often involve large and complex apparatuses containing conducting fluids made to rotate very fast.
Galitski and colleagues are now saying that the dynamo effect might be observable in a much simpler system – a hydrodynamic Weyl metal. This is a recently discovered class of topological materials in which electronic excitations behave as massless fermions.
They studied how charges (electrons and holes) travel in these metals and show that they can exhibit effects such as turbulence, the likes of which are seen in weakly viscous fluids. The charge motion in Weyl metals obeys the same equations that underlie dynamo theory – that is, the Navier-Stokes equations (which describe the hydrodynamic motion of the medium) and Maxwell’s equations of electromagnetism. Under nonrelativistic conditions, these give rise to nonlinear magnetohydrodynamics (MHD) equations that are complicated and difficult to solve.
Simplified MHD models and a large R and Rm
This problem can be overcome, however, by considering solutions of simplified MHD models. These suggest that the dynamo effect can occur when the terms in the equations that enhance the magnetic field are greater than those that enhance magnetic diffusion. These figures of merit are the all-important hydrodynamic (R) and magnetic (Rm) Reynolds numbers.
What can you do with a Weyl semimetal?
The researchers calculated these numbers for a Weyl metal and found that they can be large enough (>>1) to generate a dynamo-induced field that could be detected in experiments. Astrophysical bodies naturally have large magnetic Reynolds numbers thanks to the huge distances involved, say the researchers, and the larger the R and Rm, the more effective the dynamo action.
“The conductivity of astrophysical media varies greatly – from 10-11 S/m for interstellar plasma to 103 S/m for the solar convention shell and 105 S/m for the Earth’s core, but in all of these cases the large magnetic diffusion coefficient is compensated by literally astronomical distances resulting in large magnetic Reynolds numbers, however small the conductivities are,” they explain.
The new study, which is detailed in Physical Review Letters 10.1103/PhysRevLett.121.176603, is just the start and many electronic materials other than these 3D Dirac materials might serve as platforms for observing the dynamo effect, they say. For example, electronic metals near critical points (such as those just above a superconducting transition) represent promising systems to look at in this context. These “could pave the way to simulating in solid-state materials the effect of magnetic field excitation – a remarkable phenomenon, usually delegated to the fields of geophysics, astrophysics, and cosmology”.




