Unless one is a poet, a war hero or a rock star, it is a mistake to die young. James Clerk Maxwell – unlike Isaac Newton and Albert Einstein, the two giants of physics with whom he stands – made that mistake, dying in 1879 at the age of just 48. Physicists may be familiar with Maxwell, but most non-scientists, when they switch on their colour TVs or use their mobile phones, are unlikely to realize that he made such technology possible. After all, in 1864 he gave us “Maxwell’s equations” – voted by Physics World readers as their favourite equations of all time – from which radio waves were predicted.

Suppose Maxwell had lived one year beyond the biblical three score and ten. He would then have been alive on 12 December 1901, the day when Guglielmo Marconi, in St John’s, Newfoundland, received the first transatlantic radio signal from a transmitter in Cornwall, UK, designed by Maxwell’s former student Ambrose Fleming. Or consider relativity: mention it and everyone thinks of Einstein. Yet it was Maxwell in 1877 who introduced the term into physics, and had noticed well before then how the interpretation of electromagnetic induction was different depending on whether one considers a magnet approaching a wire loop or a loop approaching a magnet. It was from these “asymmetries that do not appear to be inherent in the phenomena” that Einstein began his work on special relativity.

Had he not died so young, Maxwell would almost certainly have developed special relativity a decade or more before Einstein. Moreover, it was through reading Maxwell’s article “Ether” in the ninth edition of the Encyclopaedia Britannica that Albert Michelson came to invent the interferometer – a new kind of instrument that he and Edward Morley used in 1887 to discover that the speed of light is the same in all directions.

So what impression of Maxwell would you have gained if you had met him in his prime, as a young Scottish undergraduate Donald MacAlister did in Cambridge in 1877? You would surely have been charmed, but perhaps also surprised to meet – as MacAlister put it – “a thorough old Scotch laird in ways and speech”. As the proprietor of an 1800 acre Scottish estate, Maxwell had all the qualities of the better kind of Victorian country gentleman: cultivated, considerate of his tenants, active in local affairs, and an expert swimmer and horseman too.

Few would have guessed that this “Scotch laird”, so disarmingly old-fashioned even in 1877, was a scientist whose writings remain astonishingly vibrant in 2006 and the greatest mathematical physicist since Newton. In addition to his work on electromagnetism, Maxwell also contributed to eight other scientific spheres: geometrical optics, kinetic theory, thermodynamics, viscoelasticity, bridge structures, control theory, dimensional analysis and the theory of Saturn’s rings. He also worked on colour vision, producing the first ever colour photograph (see box “A colourful tale”).

Even if his achievements are somewhat overshadowed in the public’s eye by those of Einstein, whose successes were marked by a great series of events last year, it is a measure of Maxwell’s standing that 2006 – the 175th anniversary of this birth – has been dubbed Maxwell Year.

From Glenlair to Edinburgh

James Clerk Maxwell was born on 18 June 1831 to Frances Cay and John Clerk – a lawyer who was the younger son of James Clerk. The Clerks were one of the most distinguished and wealthiest families in Edinburgh and both of Maxwell’s parents were steeped in the city’s culture. Yet Maxwell spent the first 10 years of his life on a country estate, Glenlair in south-west Scotland, which was then a region of extreme isolation, even lawlessness, with no nearby school. How did this happen and why do we refer not to Clerk’s equations but to Maxwell’s equations?

The answer lies in a long blood-feud between the Maxwell family and another Scottish family – the Johnstones – that dates back to the 16th century. The feud included the execution in 1613 of the eighth Lord Maxwell for the murder of the chief of the Johnstones in revenge for their killing of his father. Lacking legitimate children, Lord Maxwell bequeathed land to his illegitimate son, John Maxwell, who was himself murdered in 1639. The marriage of two of the latter’s heiresses to members of the Clerk family resulted, following complex legal settlements, in the 7000 acre Clerk estate near Edinburgh being handed down in 1798 to George Clerk (James Clerk Maxwell’s uncle) and the Maxwell name and estate to John Clerk (Maxwell’s father).

After Maxwell’s parents got married, they began developing the estate at Glenlair. But with no schools nearby and only one child to look after, his mother doubled as his schoolteacher. Her death when he was eight affected Maxwell deeply and, after two unhappy years with a private tutor, he was sent to Edinburgh Academy, where his weird accent and weirder shoes (hand made by his father) won him the nickname “Dafty”. Maxwell was also involved in a tug-of-war between two aunts over who should bring him up. Despite these setbacks, Maxwell survived and soon began to enjoy Edinburgh’s marvellous culture, especially after his father made time to come from Glenlair.

Maxwell’s first scientific paper appeared when he was just 14, which suggests that he was a terrifying mathematical prodigy. In fact, Maxwell was a very clever boy but by no means exclusively scientific. Indeed, a poem of his was published in the Edinburgh Courant six months before his first scientific paper. He wrote the latter after meeting the decorative artist D R Hay, who was searching for a way to draw ovals. The 14-year-old Maxwell generalized the definition of an ellipse and succeeded in producing true ovals identical to those studied in the 17th century be René Descartes. Maxwell’s father showed the method to James David Forbes, an experimental physicist at Edinburgh University, who realized that it was correct. Forbes then presented the paper on Maxwell’s behalf at a meeting of the Royal Society of Edinburgh – a remarkable achievement for someone so young.

Student days

Maxwell began his studies at Edinburgh University in 1847 at the age of 16. He moved to Cambridge in 1850 to take the mathematical Tripos, which lasted for three years and a term. This unusually long undergraduate career, which resulted from the different ages at which students in England and Scotland then went to university, proved entirely beneficial for Maxwell. At Edinburgh he gained a broad education centred on philosophy, while Cambridge gave him an excellent training in applied mathematics and the most gruelling examination system the wit of man has devised. At both, he encountered first-class minds.

Apart from Forbes, who gave Maxwell the run of his laboratory and encouraged his interest in colour, Edinburgh boasted Sir William Hamilton, professor of logic and metaphysics. (He should not be confused with the Irish mathematician William Rowan Hamilton.) Hamilton was a man of formidable learning, a genius at enlivening young minds, and who was famous for his teachings drawn indirectly from Kant on “the relativity of human knowledge”. However, he and Forbes were enemies; only in one place did they meet well – and that was in the mind of the young Maxwell.

Cambridge, meanwhile, was home to William Hopkins – a great teacher who became Maxwell’s private tutor – as well as the world’s leading authority on optics, George Gabriel Stokes. There was also William Whewell, the supreme historian and philosopher of science who invented the word “physicist”. As one Cambridge friend recalled, Maxwell was “acquainted with every subject upon which the conversation turned. I never met a man like him. I do believe there is not a single subject on which he cannot talk, and talk well too, displaying always the most curious and out of the way information.”

Like many clever undergraduates, Maxwell worked hard while pretending not to. However, in 1854 he just missed the coveted position of “senior wrangler” in the mathematics examination, coming second to E J Routh. Two years later Maxwell was made a fellow of Trinity College, Cambridge, before returning to Scotland in 1856 as professor of natural philosophy at Marischal College, Aberdeen, at the age of just 25. It was here that he married Katherine Mary Dewar, daughter of the principal of the college.

In 1860 Aberdeen’s two colleges – Marischal and King’s – merged and Maxwell was one of the professors let go, with a pension of £40 a year. This was not a huge sum in those days, but he did have a private income of about £2000 a year from his estate so it was nothing to worry about. Maxwell moved south to King’s College, London, before “retiring” in 1865 to enlarge Glenlair House, write his Treatise on Electricity and Magnetism and become a Tripos examiner for Cambridge. In 1871, however, he returned to Cambridge full time as the first professor of experimental physics. It was here, with funding from the seventh Duke of Devonshire, that he created the Cavendish Laboratory, which opened in 1874. Under J J Thomson, Ernest Rutherford and their successors, the Cavendish was to become one of the greatest research centres in the world.

The first grand unification

On 5 January 1865, while at King’s, Maxwell ended a letter to his cousin Charles Cay about his latest scientific work with the casual remark, “I have also a paper afloat containing an electromagnetic theory of light, which, till I am convinced to the contrary, I hold to be great guns.” The judgment was correct. More than a new theory, this was a new kind of theory that entailed completely new views of scientific explanation, unifying as it did three different realms of physics – electricity, magnetism and light. This unification of nature’s basic forces is a goal that physicists are still working on today.

Before Maxwell there had been huge progress in optics and electromagnetism but troubling questions remained in both fields. The wave theory of light, originated by Thomas Young and Augustin Fresnel, was in one sense a marvellous success, leading to a flood of new discoveries. But in another way it was a worrying failure. At least 11 alternative theories existed, each of which tried to explain Fresnel’s and other formulae in terms of an underlying ether, but, as Stokes proved devastatingly in 1862, every one of them was flawed. Part of the miracle of Maxwell’s theory was that it almost magically swept the troubles with those theories away.

A different issue hampered electromagnetism, which had been discovered by the Danish physicist Hans Christian Oersted in 1820. Oersted had found that a compass needle brought near a current-carrying wire pointed at right angles to the direction of the current, which involved a twisting motion that could not be explained by any other force. Two explanations emerged. Ampère sought to reinterpret the twisting as an attraction of a more complex kind, while Faraday, who had shown that magnetism, the electric current and the resultant force on a body act perpendicularly to each other, took Oersted’s finding as an irreducible new fact.

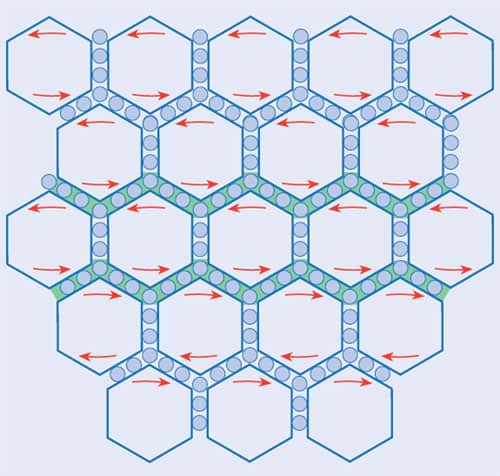
Faraday saw the “lines of force”, which are revealed by sprinkling iron filings on a sheet of paper held over a magnet, not only as geometrical lines but also, more daringly, as physical lines rather like stretched elastic bands with an extra sideways repulsion. For him, these physical stresses could be used to explain magnetic force. Maxwell developed both aspects of Faraday’s thinking, devising in his second paper in 1861 an “ether” full of tiny “molecular vortices” aligned with the lines of force. Like tiny spinning Earths, Maxwell reasoned, each vortex shrinks axially and expands sideways, giving just the stress patterns that Faraday had hypothesized (see image “mechanical model”). To explain how the vortices rotate, Maxwell envisioned smaller “gearwheel particles” meshing with the vortices.

While emphasizing that this idea, especially the gearwheel particles, was speculative and not a real physical model, he nevertheless saw it as a useful way to understand electromagnetism. In a wire, the particles are free to flow and form an electric current. In space, they serve as counter-rotating idle wheels between vortices to make successive ones turn in the same direction. This machinery gave the right result; Maxwell had “explained” magnetic force in Faraday-like terms.

Maxwell addressed the electric force – the crux of his discussion – after submitting two papers on the magnetic force for publication. The key issue was where the energy resides. Previous theories had assumed that the energy was located at or on magnets or electrically charged bodies. In Maxwell’s theory, however, the magnetic energy was in the surrounding space, or “field”, as he called it. The energy was, in other words, the kinetic energy of the vortices.

Drawing on insights from William Thomson (the future Lord Kelvin), Maxwell proceeded to make his ether elastic, with the electric force being the result of the potential energy needed to distort the ether. Intrigued by the fact that an elastic ether ought to transmit waves, Maxwell decided to calculate the speed at which they would move in terms of electric and magnetic forces, doing the calculations while at Glenlair.

On returning to London, he looked up the ratio for magnetic to electric forces, which had been determined experimentally in 1858 by the German physicist Wilhelm Weber. Weber had measured the ratio because it played an important, but not well understood, part in his own theory of electromagnetism. A velocity appeared in his theory also, but with a different numerical value that had no obvious physical meaning. Maxwell plugged Weber’s force ratio into his equations and discovered to his utter astonishment that the velocity exactly equalled the speed of light, which was then known experimentally to an accuracy of 1%. With excitement manifest in italics, he wrote, “We can scarcely avoid the inference that light consists in the transverse undulations of the same medium which is the cause of electric and magnetic phenomena.”

Having made this epoch-making discovery, Maxwell moved from his visionary model to hard fact. In a paper that has a good claim to be the foundation of dimensional analysis, in 1863 he proved that the ratio of the magnetic and electric forces indeed contains a velocity that equals the speed of light, c. The importance of this result to physics is hard to overstate. Before Maxwell, c was just one velocity among many. Now it was privileged, pointing the way forward to Einstein and relativity.

Maxwell’s vortex-ether began as an attempt at a mechanical explanation of Faraday’s magnetic stresses. Another person might have been tempted to improve and refine it. Maxwell saw that no such effort was necessary. He had by now assembled a series of equations relating electric and magnetic quantities; he could deduce wave propagation from them. Instead of explaining electromagnetism or light, he had connected these two apparently different classes of phenomena using equations that took two forms. The first, which appeared in his 1865 paper and again in his Treatise, consisted of eight groups of equations. The second, in 1868, contains the four equations that we now know as “Maxwell’s equations”. The differences are somewhat technical: the eight equations include the concept of a “vector potential” and the incorrectly named “Lorentz force law”. (Devotees of Ockham’s razor should notice a remark by Maxwell in his Treatise that “to eliminate a quantity which expresses a useful idea would be a loss rather than a gain in this stage of our inquiry”.)

Maxwell’s theory predicted many new phenomena, such as radiation pressure. But its most remarkable consequence – as Maxwell at once realized – was that it pointed to the existence of an electromagnetic spectrum. This “great storehouse of nature” might contain other radiation of higher and lower frequencies, a thought that was vindicated over the next 30 years with the discovery of radio waves, X-rays and gamma radiation. As for relativity, Maxwell introduced Hamilton’s word, in the way that physicists now understand it, in his small book Matter and Motion of 1877. Poincaré read the work; Einstein learned of it from Poincaré; and the rest is history.

From Saturn to glaciers and gases

Maxwell’s unification of electricity and magnetism was his greatest contribution to physics. But his longest ever paper concerned a different topic altogether: the nature of Saturn’s rings. In this paper, which Maxwell spent four years working on between 1856 and 1860, he showed that the rings of Saturn are not solid, liquid or gaseous but instead consist of vast numbers of independent particles. But why did he devote so much time to this particular topic?

The answer is that while Maxwell was a gentleman, he did not lack competitive drive. Coming second to Routh in the Tripos examination of 1854 was a blow, so Maxwell immediately turned his attention to another prestigious award called the Smith’s prize, which several other second wranglers, including Kelvin, had won. However, for the first time in its 84-year history, the prize that year was divided, with Routh and Maxwell bracketed equal. Maxwell therefore decided to enter the recently established Adams’ prize, awarded once every three years and open only to Cambridge graduates.

The topic for the 1856 award was the structure and stability of Saturn’s rings. It took Maxwell four years to solve the problem, but his dedication succeeded. He won the Adams’ prize with an essay that caused a stir and was a strong factor in his becoming a Tripos examiner himself six years later. Moreover, Maxwell became fascinated by the problem of dynamical stability in general. Indeed, in 1868 he decided to investigate the stability of a “speed governor” – a device that controls a motor’s rate of rotation – his paper on which was the first in the now vast field of control theory.

Then came delicious irony. Maxwell was appointed examiner of the 1877 Adams’ prize, the topic was dynamical stability and the winner was Routh, who derived, amid much else, a fundamental stability condition now known as the Routh–Hurwitz criterion.

Maxwell, together with Ludwig Boltzmann and Willard Gibbs, also created the science of statistical mechanics. His work in this area began in 1859, when he read a highly original paper by Rudolf Clausius on colliding gas molecules. However, Maxwell went much further, first obtaining a statistical law governing the distribution of velocities in the gas and then determining many properties of gases that previously were impossible to calculate. One was viscosity, which he found should remain constant over a wide range of pressures. This unexpected result was confirmed by Oskar Meyer and by Maxwell and his wife, she doing nearly all of the experimental work. In particular, she discovered that viscosity increases almost linearly with temperature, rather than as the square root of temperature as the original theory predicted.

In attempting to understand this puzzle, Maxwell made one of the most spectacular intellectual leaps in physics, which took him from gases to glaciers and back. Rudolf Clausius, picturing molecules as billiard balls, had assumed that they travel a certain average distance, known as the “mean free path”, between collisions. But that picture turned out to be too simple. In practice, longer-range forces act between molecules, accounting for the different temperature dependences. A new approach was needed. Maxwell recalled that Forbes, while climbing in the Alps, had made extensive measurements of glaciers that showed that they move like liquids over long periods of time.

Maxwell seized on this idea and introduced into physics, engineering and glaciology a far-reaching new concept known as the “relaxation time”: a glacier behaves like a solid at times shorter than the relaxation time, but like a liquid at longer times.

Maxwell then showed mathematically that molecules in a rarefied gas bouncing from wall to wall also act like a solid. In other words, as pressure increases, a gas begins to behave like a fluid and has a relaxation time that increases with pressure. Clausius’ characteristic distance could therefore be replaced by a characteristic time, and Maxwell was able to develop the theory on a firm mathematical footing, which was later extended by Boltzmann.

Present throughout, alas, was a problem. In his first paper on this subject, Maxwell had proved a neat theorem that stated that the average rotational and translational energies of molecules are equal. When used to predict the specific heats of gases, however, the theorem gave results that flatly disagreed with experiment. Deeply alarmed, Maxwell said in a lecture at Oxford in 1860 that this finding “overturns the whole theory”. Although this was not true, he had discovered the first breakdown of classical mechanics.

Worse was to follow. When Boltzmann extended the theory, he established a much wider principle, equipartition, that applied to all modes of motion, internal and external, of molecules. A student at Cambridge in the 1870s vividly recalled Maxwell saying that “Boltzmann has proved too much”, explaining his remark with the observation that equipartition would apply to solids and liquids as well as gases. Only with the arrival of quantum mechanics was that anxiety transformed from difficulty to triumph.

The issue of equipartition steadily worsened. In a review written in 1877 Maxwell examined and demolished every evasion advanced up to that time, concluding that nothing remained but to admit “the thoroughly conscious ignorance that is the prelude to every real advance in knowledge”. The answer – and new questions – came in 1900 with Planck’s quantum of action. Some 40 years after Maxwell’s alarming discovery of 1860, the prediction of the specific heat of gases and much else was explained by the fact that the energy is quantized. At the atomic and subatomic levels, equipartition does not hold.

Maxwell’s legacy

When Einstein visited Cambridge in the 1920s, someone remarked, “You have done great things but you stand on Newton’s shoulders.” His reply was, “No, I stand on Maxwell’s shoulders.”

He was correct, but much else in modern physics also rests on Maxwell. It was after all Maxwell who introduced the methods that underlie not only Maxwell–Boltzmann statistics but the quantum-mechanical Fermi–Dirac and Bose–Einstein statistics governing photons and electrons. It was even he, in two innocent-seeming discussions in the 1870s, who first emphasized what we now call the “butterfly effect” – the fact that tiny differences in initial conditions can produce huge final effects, the starting point of chaos theory. In a similar vein, Maxwell’s scientific contributions have had dramatic effects on the future course of physics, notably the quest to unify nature’s fundamental forces. Sadly Maxwell died of cancer on 5 November 1879 and never lived to see the applications of radio or the demystifying of equipartition. But the power of his scientific insights lives on.

A colourful tale

Few people will be aware that James Clerk Maxwell produced the first ever colour photograph (left, of a tartan ribbon). But Maxwell had a life-long interest in optics and colour vision, beginning in 1849 when the Edinburgh University physicist David James Forbes spun a top with three adjustable coloured sectors. Both men knew that red, blue and yellow are primary colours. However, no combination of those colours produced grey. (Thomas Young knew this years earlier but that fact had been forgotten.)

What was needed were red, blue and green. Improving Forbes’ top, Maxwell determined “colour equations”, which give quantitative measurements of the ability of the eye to match real colours. But since light conditions vary for different observers, Maxwell realized that a more sophisticated instrument than a top was needed, which led to him inventing an ingenious “colour box”. With it, he and his wife carried out detailed measurements of the variations of colour register across the retina for hundreds of observers – an achievement unmatched until the 1920s. On 17 May 1861 Maxwell gave a lecture on colour at the Royal Institution in London, during which he projected through red, green and blue coloured filters three photographs of a tartan ribbon taken through the same filters. This first-ever colour photograph was a surprisingly faithful reproduction of the original.

At a Glance: James Clerk Maxwell

• James Clerk Maxwell was born 175 years ago, in recognition of which 2006 has been dubbed Maxwell Year
• A child prodigy, he studied at Edinburgh and Cambridge universities and was appointed professor at Marischal College, Aberdeen, 150 years ago, aged just 25
• In 1865 Maxwell wrote down his famous equations, which related – or “unified” – electricity, magnetism and light for the first time
• He played a key role in the development of statistical mechanics, paving the way for the development of quantum mechanics
• Maxwell was a cultivated man who could speak on almost any intellectual topic, yet he also took a keen interest in the local affairs of his Scottish estate

More about: James Clerk Maxwell

S G Brush, C W F Everitt and E Garber (ed) 1983 Maxwell on Saturn’s Rings (MIT Press)
S G Brush, C W F Everitt and E Garber (ed) 1986 Maxwell on Molecules and Gases (MIT Press)
C W F Everitt 1975 James Clerk Maxwell: Physicist and Natural Philosopher (Scribner)
E Garber, S G Brush and C W F Everitt (ed) 1995 Maxwell on Heat and Statistical Mechanics (Lehigh University Press)
P M Harman (ed) 1990–2002 The Scientific Letters and Papers of James Clerk Maxwell (three vols) (Cambridge University Press)
B Mahon 2004 The Man Who Changed Everything: The Life of James Clerk Maxwell (Wiley)