Soft matter and liquids

When I read scientific papers, I often end up pondering questions that are – in the grand scheme of things – mere footnotes and details. Quite simply, I lose sight of the big issues. Fortunately, one benefit of teaching physics to undergraduates, as I do, is that it lets me take a broader perspective. Take the way that textbooks deal with the fundamental differences between the states of matter. While these works contain neat and cohesive descriptions of gases and solids, many struggle with liquids.

Consider David Tabor’s classic book Gases, Liquids and Solids, which has been reprinted many times since it was first published in 1969. “The main characteristics of [the gaseous and solid states] are well understood,” Tabor writes. “By contrast the liquid state, in some ways, has ‘no right to exist’ [and] raises a number of very difficult theoretical problems.” Then there’s Franz Mandl’s 1971 book Statistical Physics, in which he discusses the qualitative differences between liquids and solids, but then throws in a disclaimer that his argument is “not accepted by everyone”.

As we can see, scientists’ confusion regarding the description of the liquid state has been bubbling beneath the surface for decades. But if you think we have a problem understanding liquids, the situation is even worse with the “supercritical fluid” state, which I’ll come to later. However, recent advances mean we could resolve these problems and provide theoretical descriptions of both the liquid and supercritical fluid states over the wide range of pressures and temperatures that they exist across.

Liquids – what a gas!

While some physicists have tried to describe the liquid state directly from first principles – that is to say, without referring to the solid or gas states – this approach is very difficult. In a crystalline solid, the high level of order makes calculations and computations relatively easy. In a gas, the lack of any structural order is used to simplify calculations and computation instead. However, to fully understand the liquid and supercritical fluid states, neither option can be used. Instead, what researchers usually do is to use gases as a starting point and make some adjustments.

One way to do this is to wheel out the Van der Waals equation of state. In this approach, a sample is described as a non-ideal gas, in which the particles have a specific size (rather than being infinitely small point masses) and there is an attractive Van der Waals force between them. By applying this equation to liquids, you can understand boiling as a “first-order” phase transition, which means that as it turns from liquid to gas, there is a discontinuous (rather than smooth) jump in the material’s properties, such as its density, heat capacity and entropy.

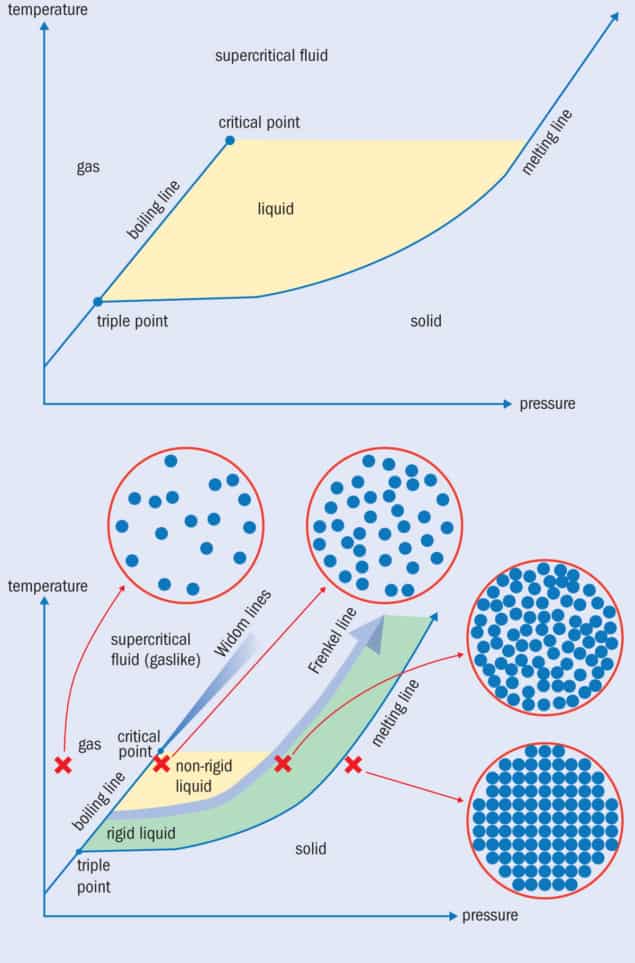
However, physicists are not interested only in what happens to a liquid at a single pressure. If you raise the pressure, the boiling temperature goes up too, with the line dividing the two states of matter on a temperature/pressure graph being known as the “boiling line” (figure 1a). What’s interesting is that as you go up in pressure, the jump in the liquid’s density, heat capacity and entropy as it boils becomes steadily smaller. Eventually, when the pressure is sufficiently high, a “critical point” is reached, beyond which there is no boiling transition at all. With no phase transition between liquid and gas states, the sample is now a supercritical fluid, a still-mysterious phase that shares properties of both a liquid and a gas.

Most textbooks leave liquids and supercritical fluids at that; but the supercritical fluid state has a complexity that physicists are only now starting to appreciate. For starters, parameters such as density, which usually change abruptly and discontinuously when we cross the boiling line, do something different if we make a transition above (albeit close to) the critical point. They still change over a narrow range of pressure or temperature but now do so continuously, not in a jump.

What this means is that the boiling line can now be extended beyond the critical point, where it is dubbed the “Widom line”, in honour of the Cornell University chemist Benjamin Widom (figure 1b). Indeed, we can plot out separate Widom lines for all the different properties that change when we boil a liquid, including its density, speed of sound and heat capacity. The Widom line links the different pressure-temperature points where there is a narrow change in each property. They start at the critical point but gradually diverge from each other and get smeared out.

Interestingly, if we increase the pressure on a liquid or supercritical fluid at a fixed temperature the sample always eventually solidifies. Nitrogen, for example, becomes a solid at room temperature if you squeeze it to about 24,000 bars pressure (2.4 × 10⁹ N/m²). Even hydrogen solidifies at room temperature if you take it to 55,000 bars. Using modern equipment, such as the diamond anvil cell, these kinds of experiments are routine; we really can take air from the atmosphere and freeze it solid.

But the problem is that long before it solidifies, the fluid becomes so dense that we can no longer describe it as being similar to a gas. For instance, in dense molecular fluids, such as water, neighbouring molecules will slot together in an ordered manner over short distances almost exactly like they do in solids. What’s more, a variety of experiments dating back to the 1960s have shown that dense fluids support shear waves. Both types of behaviour are totally different to what is observed in gases and in liquids near the critical point.

A solid start

As it is hard to describe these kinds of liquids and fluids by starting off with the behaviour of a gas, some physicists have instead tried to liken them to solids. Various theoretical descriptions of this ilk have been put forward over the decades or, if you include Maxwell’s work, over the centuries. Based on this solid-based approach, researchers have recently been able to model properties of dense fluids, discovering that they take on certain solid-like properties as you raise the pressure (P) or lower the temperature (T). Surprisingly, the onset of these properties occurs within a relatively narrow P–T range.

This narrow P–T range has been named the “Frenkel line” (figure 1b) after the Soviet physicist Yakov Ilyich Frenkel (1894–1952), who pioneered the solid-like theoretical approach to liquids. But what do we know about liquids beyond the Frenkel line? At the critical point, there is just enough room to squeeze in an additional particle in-between two adjacent particles. But when the Frenkel line is crossed, experiments show that the liquid takes on a relatively close-packed structure and has a density not much less than that of a solid.

The Frenkel line at the critical temperature is therefore crossed at a much higher pressure than the critical pressure (figure 2). And as well as extending into the supercritical region at high temperature, the line should continue below the critical temperature and can in fact pass underneath the critical point. On the high-pressure side of the Frenkel line, it turns out that the sample is so stiff that some (though not all) shear waves can pass through such that it’s now termed a “rigid liquid”. As you heat the fluid, it takes more and more pressure to force it into the rigid-liquid state but you can still liquefy it far beyond the critical temperature. That to me is amazing: a liquid can exist at far higher temperatures than we previously believed. Indeed, the only reason for the Frenkel line to end is when the sample becomes so hot it turns into a plasma instead.

As for what happens on the low-pressure side of the Frenkel line, the liquid is in a more conventional, textbook-like non-rigid state. Some researchers claim that the non-rigid liquid state can also persist above the critical temperature, albeit not to such high temperature as the rigid liquid state. After all, the Widom line is simply the thermodynamic continuation of the boiling line. However, in my view – which, to quote Mandl, is not accepted by everyone – there are two flaws with this argument.

First, some properties, such as density, change as you cross the Widom line in a way that is qualitatively similar to what happens when you cross the boiling line. But other properties, such as heat capacity, change in a qualitatively different way in the two cases due to the complex and unique nature of fluids near the critical point. So the changes we make to the fluid when we increase pressure across the boiling line beneath the critical point into the non-rigid liquid state are not the same as the changes we make to the fluid when we increase pressure to cross the Widom line above the critical point.

The other reason I am not convinced that the non-rigid liquid state can persist above the critical temperature is the amount of thermal energy the particles have. Most particles have enough thermal energy to escape the attractive forces binding them to their neighbours. That’s why we call the sample a supercritical fluid rather than a liquid. The only way you can liquefy a supercritical fluid above the critical temperature is to make the sample so dense that there’s nowhere for the component particles to escape to. That means crossing the Frenkel line, not the Widom line.

Controversial claims

While researchers may argue about the significance of the Widom line, and how far it extends from the critical point, there is no dispute that it exists. That’s because the properties of fluids near the critical point have been studied in detail for decades due to their industrial importance in applications such as power generation, food processing and refrigeration. Those studies culminated in an online database of fluid properties, held by the US National Institute of Standards and Technology.

The Frenkel line, on the other hand, is a newer and more controversial concept. While experiments have shown that dense fluids and liquids can exhibit solid-like properties, such as being able to support shear waves, there have been very few systematic studies of how suddenly these properties pop up. In fact, we’re not even sure if they appear over a narrow enough range of pressures and temperatures to justify calling it a Frenkel “line”.

Recently, however, researchers at the University of Köln in Germany led by Clemens Prescher have studied how X-rays diffract when fired into fluid neon at ambient temperature, which is so far beyond the critical point of neon that only the Frenkel line could be reasonably expected to cause any narrow crossover in fluid properties (Phys. Rev. B 95 134114). They found that medium-range order (a characteristic expected for dense fluids on the high-pressure side of the Frenkel line) appeared rather abruptly, proposing that there was a sufficiently sudden change in properties to justify calling the transition the “Frenkel line”.

Meanwhile, my colleagues and I at the University of Salford were carrying out experiments in our own lab when we found something extraordinary. You don’t get many “Eureka!” moments in science, but this was one of them. We were working late into the evening – don’t tell the health-and-safety people – studying methane using optical spectroscopy. We were far above its critical temperature when we dropped the pressure to see what would happen. To our astonishment, we found that the vibrational frequency and other spectral characteristics changed abruptly.

The properties went from those expected from a rigid liquid (dominated by the repulsion between particles that have been forced far closer together than their equilibrium separation) to those expected from a gas-like sample (where attractive Van der Waals forces between particles dominate). These drastic changes indicated that we had crossed the Frenkel line and gone from the rigid liquid state and into the gas state. Then the computer crashed. We’d lost our data. Fortunately, we were able to repeat the experiment and confirm our finding (Phys. Rev. E 96 052113).

Read more

The secrets of the blue fog

These investigations will continue – not least because the applications of this research are so exciting. For example, if a liquid or fluid can support shear waves – as Frenkel’s solid-like description of the liquid and dense-fluid states suggests – then the sample has an additional way for it to store heat. This may sound mundane, but it is crucial if we are to understand how heat is stored in the planets Jupiter, Saturn, Uranus and Neptune. In recent years researchers have used Frenkel’s theoretical framework to accurately model the observed trends in fluid heat capacity as pressure and temperature are changed.

Frenkel proposed that dense liquids are a relatively close-packed structure in which, most of the time, particles oscillate around a certain equilibrium position. However, he added, a particle can occasionally swap places with an adjacent particle or hole. Physicists have proposed that the average time a particle spends in an equilibrium position between jumps – known as the “liquid relaxation time” – corresponds to the maximum period of a shear wave that can be supported by the fluid. This time will vary a lot with temperature and we can model the observed heat capacities of fluids by accounting for this. It turns out that when we turn up the temperature, the liquid relaxation time falls. In other words, the liquid can support fewer shear waves as it gets hotter and the heat capacity falls. In fact, the specific definition of the Frenkel line is that it is crossed on temperature increase when the liquid relaxation time becomes so low that no shear waves can pass through the fluid.

Another application of this work is to do with how fluids mix. Gases are always miscible, whereas liquids are miscible only in certain cases. Their behaviour in this regard is therefore more like solids given that only certain combinations of elements will form solid solutions (single-phase alloys). What we now want to explore is miscibility throughout the supercritical fluid phase: does the Frenkel line affect miscibility of fluids? This is not just exciting terra incognita in terms of basic physics, but could also be the most important consequence of the Frenkel line in planetary science. After all, Jupiter, Saturn and the other outer planets are diverse mixtures of different fluids and no-one really knows how well they mix together.

Before we get too excited about the future prospects for this research, I should point out that generating and measuring the required conditions is experimentally challenging. The pressures are beyond the reach of gas compressors and large-volume cells, but too low for the diamond-anvil cell, which struggles to even measure the required pressures. These problems get worse at high temperatures.

However, the most important point for me about the current situation is just how little we really understand about liquids. In the last five years, scientists have argued openly in the literature about how we define the liquid state and under what conditions we consider a sample to be in the liquid state (see, for example, J. Phys. Chem. Lett. 8 4995 and Physica A 478 205). The fact that the answers to these basic questions are still up for debate is, to me, extremely exciting. But once we get answers, it will – I hope – be a chance to rewrite the textbooks.