Topological materials – materials whose surface properties are very different to those in their bulk – have come to the fore in recent years and are currently revolutionizing modern condensed matter physics thanks to their unique properties.
Topological phases of matter are so-called because they are described by global invariants that are not at all affected by imperfections, such as defects or other variations, in a material. Mathematically, these invariants are constructed as integrals of a local property over a closed parameter space. And although they show much promise for use in a host of applications, including error-resistant spintronics and quantum computation, they have been considered as global, and not local, quantities thus far.
Existing picture may be wrong
A team of researchers at the University of Chicago in the US has now succeeded in measuring no less than three topological invariants of a quantum Hall type of material system, all with spatial locality. “Normally, topological invariants are quantities that require us to know details about the entire system in question,” explains study lead author Nathan Schine of the James Franck Institute and the Simon Lab at the Department of Physics. “For instance, you cannot know the knottiness of a loop of string without first seeing the entire string. This is how we think about topological invariants in physical materials, but recent research suggests that this picture may be wrong.”
The first topological invariant that the researchers measured is the Chern number, which directly provides a value for the electrical conductance (that is, how much electric current flows in response to an applied electric field). The second is the mean orbital spin, a bulk invariant that quantifies the magnetic-like coupling of a particle to curvature and which is related to the Hall viscosity and Wen–Zee shift. The third is chiral central charge, which is abstractly related to gravity, is equal to the total number of edge modes (neutral and charged) in integer quantum Hall and Laughlin states, and gives rise to the thermal Hall conductance. The mean orbital spin and the chiral central charge are similar to the Chern number in the way they are defined.
Very difficult to access
“The topological invariants we have measured are typically very difficult to access because just making a clean, low-disorder quantum Hall material is a big challenge in itself,” says Schine. “So, rather than fabricating a solid-state device, we built our material out of photons that we can trap and imbue with an effective mass by placing them inside an optical resonator.”
The resonator is made from high-reflectivity mirrors pointing at each other, he explains. Inside this structure, light can bounce back and forth thousands of times before being absorbed or scattered out.
“By engineering the geometry of the resonator, we make the trapped photons behave like electrons in a quantum Hall material,” he tells Physics World. “This means that these photons have the same sorts of topological structure that electrons would have in a regular quantum Hall material.
Unusual mathematical description
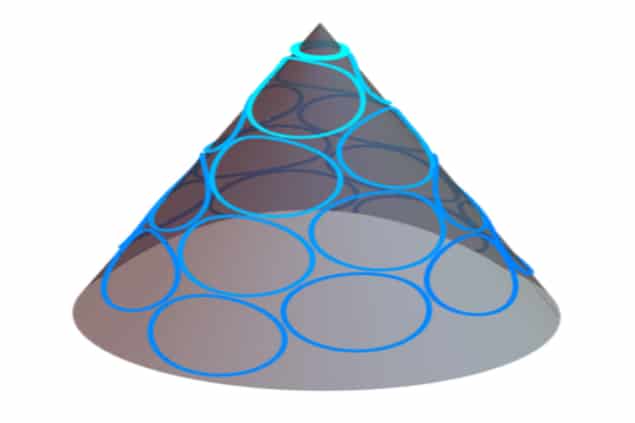
“However, because we use photons, we can go further and actually engineer the space through which the photons move, for example, so that it is curved like the surface of a cone. We then look at how much light transmits through this resonator as a function of the frequency of the light and where the light hits the resonator. This data contains information about the topological invariants since introducing a conical geometry (and then threading the cone tip with a small tube of magnetic flux, as in our experiments) produces a localized density response that strongly depends on both the mean orbital spin and the chiral central charge.”
The researchers say they made use of an unusual mathematical description of the Chern number in their work that goes back over a decade in a paper published by Alexei Kitaev. “This description is directly related to the types of local measurement that we perform in our lab,” says Schine.

3D topological insulators go photonic
Magnetic lengths
The Chicago team also discovered that the three invariants it measured converge to their global values when probed over increasing length scales – over several “magnetic lengths” in fact. This result agrees with what is expected for a topological insulator.
“Magnetic lengths are an important length scale in quantum Hall materials and in our system, one magnetic length is approximately 53 microns,” explains Schine. “Researchers usually describe quantum Hall systems as being comparable to or larger than this length and such a system has well defined and constant topological properties. The idea of convergence describes how topological invariants take on their expected values as the system size increases from smaller-than to greater-than the magnetic length.”
This idea is not very different to that of a solid crystal having the length scale of the crystal lattice spacing, he says. “It does not make sense to talk of a diamond crystal containing only one carbon atom, but once you have a system size of many lattice spacings, you have many carbon atoms and can so describe a diamond crystal – and start to think about its properties.”
The researchers, reporting their work in Nature 10.1038/s41586-018-0817-4, say they are now busy building more complex topological materials out of light. “These materials should have some very interesting and unique properties and the measurement techniques we have employed so far will be critical to measuring these and understanding their topological order.”