Subtle physics is needed to explain many of nature’s mysterious atmospheric optical phenomena, including rainbows, ice-crystal haloes and the much rarer fog-bows, dew-bows and glories. John Hardwick investigates
In his poem of 1820 entitled Lamia, John Keats complained that cold philosophy had destroyed the mystery of nature, and that Newton, through his work on optics, had “unweave[d the] rainbow”. Such a sentiment would find little sympathy with most scientists – or with many artists today for that matter. Indeed, an understanding of natural phenomena can only enhance our appreciation of nature and art.
Although it has long been known that a rainbow is produced by the dispersion of white light through rain droplets via refraction, there is far more to this optical phenomenon than first meets the eye. More complex and subtle interactions between light and water droplets can also create the “fog-bow”, the “dew-bow” and the “glory”.
Rainbows explained
Despite being a familiar sight (figure 1), rainbows are much harder to understand than one might think. The ingredients are, of course, sunlight and rain droplets. Although the Sun’s rays that reach the Earth are essentially parallel, the light impinges on a spherical droplet at a wide range of angles to the surface, where it undergoes refraction. When the light reaches the back of the droplet, two things can happen (figure 2a). The light can either refract and continue in a forward direction out of the drop, or it can be reflected internally, before passing back out through the front surface of the droplet via another refraction. It is this second process – in which light is refracted, reflected and refracted again – that creates the rainbow, which explains why rainbows only appear when one looks away from the Sun into a rain shower.
1 Bow beautiful
Photograph of a rainbow taken by the author using a 45 mm lens at the Daresbury Laboratory, UK, in 1976.
There are, however, innumerable raindrops at many different heights and positions above the horizon. As a result – and because of the many different angles at which the sunlight strikes the droplets’ surfaces – we receive light rays at many different angles to the “antisolar direction”, which is the direction looking away from the Sun towards the shadow of our head. So why does the bright, coloured arc of the rainbow only appear centred on this direction and at a specific and narrow range of angles to it?
Consider first what happens when the incident light strikes the surface of a droplet head on. Some of the light continues straight through the drop, while the rest reflects directly back. For the latter, the “angle of deviation” between the incident and reflected beams is 180°. But as the incident light strikes the droplet at a larger angle, the angle of deviation falls below 180°. When the incident light strikes at even larger angles, the deviation eventually reaches a minimum value, before rising again (figure 2).
2 Rainbow optics
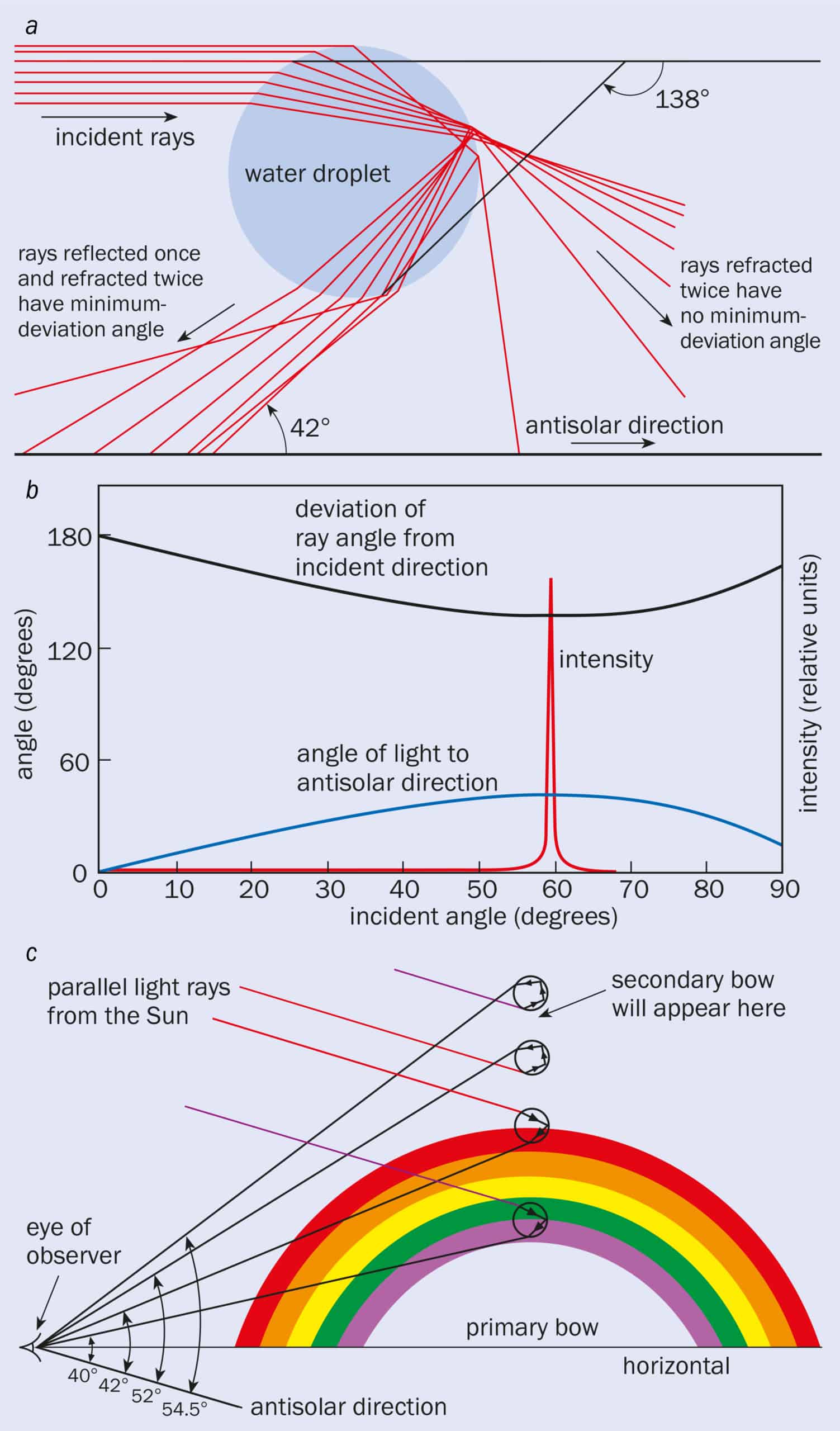 (a) A parallel beam of sunlight striking a spherical rain droplet. Despite being parallel, the light strikes the droplet at a wide range of different angles. The light undergoes refraction as it enters the droplet before undergoing reflection and further refraction. (b) The “angle of deviation” (black line) between the incoming and outgoing rays passes through a minimum value for each wavelength, which is 138° for red light. The intensity of the deviated light (red line) reaches a maximum at this angle and is responsible for the creation of a “primary” rainbow. (c) Different colours have different minimum-deviation angles because the refractive index of water depends on wavelength. The angle between light from the primary rainbow and the “antisolar direction” is 42° for the red bow and 40° for the violet bow. A separate, less intense, “secondary” bow can also be created from light that undergoes not one but two reflections from inside the droplet. The colours of this bow appear in reverse order to the primary bow.
(a) A parallel beam of sunlight striking a spherical rain droplet. Despite being parallel, the light strikes the droplet at a wide range of different angles. The light undergoes refraction as it enters the droplet before undergoing reflection and further refraction. (b) The “angle of deviation” (black line) between the incoming and outgoing rays passes through a minimum value for each wavelength, which is 138° for red light. The intensity of the deviated light (red line) reaches a maximum at this angle and is responsible for the creation of a “primary” rainbow. (c) Different colours have different minimum-deviation angles because the refractive index of water depends on wavelength. The angle between light from the primary rainbow and the “antisolar direction” is 42° for the red bow and 40° for the violet bow. A separate, less intense, “secondary” bow can also be created from light that undergoes not one but two reflections from inside the droplet. The colours of this bow appear in reverse order to the primary bow.
At the minimum-deviation angle the rate of change of deviation angle with incident angle is zero. What this means is that light striking a droplet over a relatively wide range of incident angles emerges concentrated in a narrow – and almost parallel – direction. For example, light rays spanning a 13° interval around the incident angle for minimum deviation are focused down to an emerging beam with an angular width of just 1°. Light travelling in this direction has a relatively high intensity and forms part of the standard – or “primary” – rainbow with which we are all familiar.
Different colours have slightly different minimum deviation angles; it is about 140° for short-wavelength violet light and falls to 138° for red light. The violet component of a primary rainbow is therefore on the bow’s inner side – about 40° to the antisolar direction – while the red component is on the outside at about 42° (figure 2c). Other colours fall in between. As the Sun rises, all that changes is that we see less and less of the rainbow’s arc as the “antisolar point” – the centre of the circle of which the rainbow is a part – and the outer limbs of the bow gradually sink below the horizon. Interestingly, if the Sun is higher than 42° above the horizon, minimum-deviation rays can only be received from drops located at angles below it, which is why rainbows are generally not visible when the Sun is high in the sky at the middle of the day.
Another interesting property of a primary rainbow is that the intensity of light coming from below it is higher than the background intensity from above it. This effect is visible in figure 1. The reason for this is that rain droplets cannot contribute to any light coming from angles above the rainbow because light cannot be bent round a droplet by less than the minimum angle of deviation. Some of the light scattered by the raindrops can, however, reach the observer from below the rainbow, which is therefore brighter than the area above it – but, of course, not nearly as bright as the rainbow itself.
Although a large proportion of light exits the drops after a single internal reflection to form the primary rainbow, some light can undergo two internal reflections. Such twice-reflected rays, which also have minimum-deviation angles and associated intensity maxima, form a “secondary” bow. This appears above the primary bow at an angle of about 52° to the antisolar direction. The secondary bow is fainter than the primary bow and its colours appear in the reverse order. A secondary bow is just visible in figure 1.
What about those light rays that pass out through the droplets in the forward direction after two refractions and no reflection? These have no minimum deviation, which means that this light does not reach a maximum intensity at any particular angle. In other words, if we look towards the Sun through rain, we will see no bright rainbow but just an overall forward glare.
However, in principle, a “tertiary” bow can also be formed after the light has undergone three internal reflections in a droplet. This would occur when looking towards the Sun at an angle of about 40°, but it would be fainter than the secondary bow and obscured by forward glare. There have been some reported sightings of a tertiary bow (D E Pedgley 1986 A tertiary rainbow Weather 41 401) but no photographs exist, so far at least!
Supernumeraries and fog-bows
While the main features of a rainbow can be explained by considering the refraction and reflection of light rays, this cannot be the whole story. For example, the intensity of light at the minimum-deviation angle tends to infinity when plotted at finer incident-angle increments. This is clearly not true in reality. Moreover, faint, pale “supernumerary” bows can sometimes be observed below the primary rainbow itself. These are concentric circles of smaller radius than the main rainbow.
The answer to these puzzles lies in the fact that light is not a ray but a wave. When this is taken into account, the unwanted infinity in intensity disappears and is replaced by a maximum in intensity close to the minimum-deviation angle. This maximum can be regarded as a first-order diffraction peak created by the interference of different parts of the wavefront that have reflected off different parts of the droplet’s back surface, have travelled exactly the same distance and are in phase.
Other parts of the wavefront will have different pathlengths, one wavelength more (or less) than the other, and will interfere to create less intense second- and higher-order diffraction peaks, which are the supernumerary bows. The path difference depends on the size of the droplets, which means that supernumeraries are most easily visible when the rain droplets are nearly all the same size. If the droplets were not uniform, the supernumerary bows from different-sized drops would have different angles and could not be clearly distinguished. A search for the origin of supernumerary bows helped in the development of the wave theory of light. This work eventually enabled George Airy, then Britain’s Astronomer Royal, to solve the problem of infinite intensity and explain supernumeraries in 1838.
Wave theory can also explain a rarer form of bow, known as a “fog-bow”. If the rain droplets are large – say about 1 mm in diameter – the first-order diffraction peaks for the different colours of the rainbow are narrow and well separated, which means that the individual colours can be clearly distinguished. However, if the raindrops are smaller than about 50 µm in diameter, the bows of different colours become so broad that they overlap. What one sees in this case is a single, broad white arc. Could this fog-bow be what appears in the famous Buttermere Lake painting by the British artist Joseph Mallord Turner? It shows a white bow above Cromackwater and Buttermere in the Lake District (figure 3).
3 Fog-bow or not?
 J M Turner’s 1798 painting Buttermere Lake, with Part of Cromackwater, Cumberland, a Shower shows what appears to be a “fog-bow”. It is created when rain droplets are so small that the different-coloured bows become broadened by diffraction and start to overlap. The painted rainbow is too narrow in width to be a fog-bow. Closer inspection reveals that it also has an anomalously small radius. Turner appears to have been using artistic licence to create the image he wanted. (Courtesy: Tate, London)
J M Turner’s 1798 painting Buttermere Lake, with Part of Cromackwater, Cumberland, a Shower shows what appears to be a “fog-bow”. It is created when rain droplets are so small that the different-coloured bows become broadened by diffraction and start to overlap. The painted rainbow is too narrow in width to be a fog-bow. Closer inspection reveals that it also has an anomalously small radius. Turner appears to have been using artistic licence to create the image he wanted. (Courtesy: Tate, London)
But while Turner’s bow is white – and so looks like a fog-bow – the width of the white band is much less broad than is expected for a fog-bow; it is instead about as narrow as the coloured band of a rainbow. On closer inspection the painting is even more curious. It represents a view from near Rannerdale and contains, on the left, a mountain called Fleetwith Pike, which is 544 m above the level of the lake and some four miles in the distance. The angle subtended by the mountain’s vertical extent above the lake is about 5°. If we imagine that the picture has been taken by a camera, the distance from the lake to the summit on the printed page gives us the effective focal length of the camera and, in turn, the angle subtended by the rainbow. A simple calculation indicates that the white bow has an angular radius of about 7.5° – some five times smaller than a standard rainbow (42°).
The colour and anomalous size of the fog-bow are probably because Turner was using artistic licence to create the image he wanted. Indeed, Turner is known to have painted a white rainbow above the forum in Rome, which – based on the shadows that also appear in the picture – was physically impossible (R Lee and A Fraser 2001 The Rainbow Bridge: Rainbows in Art, Myth and Science).
The halo
Raindrops are not, of course, the only form of precipitation. Light can also refract through ice crystals falling through the air. If the crystals all have the same shape, light refracting through them can create a similar effect to the rainbow – a bright, sometimes coloured, bow known as a “halo”. But what causes the phenomenon of minimum deviation, which plays such a key role in the formation of a rainbow? It appears to be ruled out because a single face of an individual crystal forms only one angle of incidence with the rays from the Sun. The answer lies with the fact that the ice crystals tumble through the air, which orients their axes in random directions. Sunlight can therefore strike the crystal faces at many different angles of incidence, allowing minimum deviation to occur.
The most common halo is formed when light passes through an ensemble of poorly aligned hexagonal crystals, which have internal face angles of 120°. Light enters through one face of the crystal and is bent so that it leaves not via the neighbouring face but the next-but-one face. In other words, the crystal is acting like a 60° prism. Simple ray optics reveals that there is a minimum-deviation angle for light passing through such a crystal of roughly 22°. The halo therefore appears when looking towards the Sun and forms a circle of light, where the angle between the direction of the Sun and any point on the halo is 22°. Furthermore, the colours appear in the reverse order compared with a standard rainbow, because there is no reflection off the inside of the crystal’s faces. In practice, however, only the faint inner red rim is usually visible (figure 4).
4 Haloes

Haloes are created when sunlight is refracted and reflected by ice crystals in the atmosphere. The 22° halo, which is seen when looking towards the Sun, is formed from light that refracts through one face and then leaves the crystal by the next-but one face. This photograph of a halo was taken with a 40 mm lens above Zermatt in Switzerland in March 2003. The angle of deviation between the sunlight and the light leaving the crystals is estimated to be 22°. The glare from the Sun has been blocked out by the flag.
The phenomenon of minimum deviation is not the only mechanism that causes haloes. Intensity enhancements in certain directions can also be created by ice crystals as they become aligned while falling through the air. Thin hexagonal plate crystals, for example, will tend to align with the plates horizontal but with the thin, side faces of the hexagon having no preferred angle to the Sun’s direction. This will cause bright regions, dubbed “mock suns”, to appear at the sides of the circular halo. These features can appear as red and yellow smudges of light, without any accompanying circular halo, at an angle of 22° or more from the Sun along the horizontal line through the Sun.
Although one might associate haloes with winter, they can sometimes be seen in the UK during the summer when cirrus clouds are present. These clouds are so high in the atmosphere that they contain ice crystals. I have even seen photos of haloes taken as far south as Corsica in June. But, as one might expect, the most dramatic haloes appear in polar regions, where conditions can be ideal for creating large amounts of ice crystals. Indeed, the geometric theory of haloes was determined as early as 1847 by the French scientist Auguste Bravais, who analysed observations that he and others had made in the Arctic. His work is all the more remarkable considering that these observations were made in the field, without any photographic records whatsoever. Photography for use outside a studio was not developed until the end of the 19th century.
The Whymper apparition
Perhaps the most famous halo was that reported by Edward Whymper following the first ascent of the Matterhorn on 14 July 1865. During the descent, one of the climbers in the forward party slipped and dragged down the other three men to whom he was attached. The rope securing the forward party to the rest of the team then snapped and the four fell down the north face of the mountain to their deaths. Shortly after this tragic incident, Whymper and his two Swiss guides – the Taugwalders – observed an amazing apparition (figure 5a). “A mighty arch appeared, rising…high into the sky,” Whymper later wrote. “Pale, colourless, and noiseless, but perfectly sharp and defined, except where it was lost in the clouds, we watched with amazement the development of two vast crosses, one on either side.” Awestruck, Whymper recognized the phenomenon to be a type of fog-bow that was formed in the opposite (antisolar) direction to the Sun. Although the apparition had no link with the accident, the timing seemed supernatural.
5 Whymper apparition
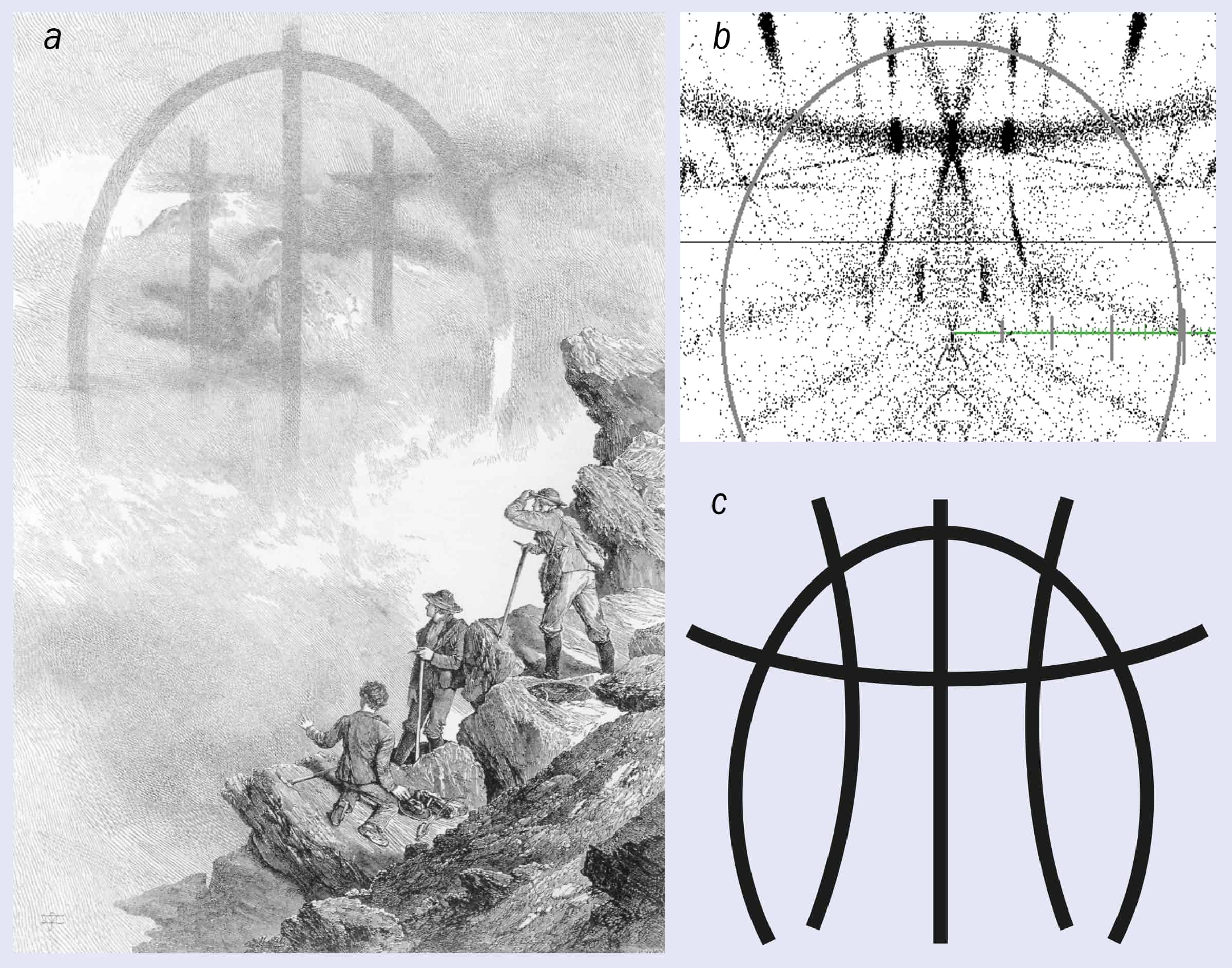 (a) This woodcut from The Ascent of the Matterhorn (1880, John Murray) shows the magnificent apparition that was reported by Edward Whymper shortly after the first successful ascent of the mountain in 1865. The apparition may have been created by a combination of a fog-bow and ice-crystal arcs. (b) This computer simulation of the Whymper apparition, which was generated using the HALO3 software developed by Les Cowley and Michael Schroeder, was created by the author by tracking the path of light through various arrangements of hexagonal ice crystals (see main text for details). (c) Whymper later drew this sketch of the apparition, which the simulation matches a little better than the woodcut.
(a) This woodcut from The Ascent of the Matterhorn (1880, John Murray) shows the magnificent apparition that was reported by Edward Whymper shortly after the first successful ascent of the mountain in 1865. The apparition may have been created by a combination of a fog-bow and ice-crystal arcs. (b) This computer simulation of the Whymper apparition, which was generated using the HALO3 software developed by Les Cowley and Michael Schroeder, was created by the author by tracking the path of light through various arrangements of hexagonal ice crystals (see main text for details). (c) Whymper later drew this sketch of the apparition, which the simulation matches a little better than the woodcut.
In a recent paper I have speculated on the possible origins of the Whymper apparition (J Hardwick 2002 Simulation of the Whymper apparition Weather 57 457). Using the HALO3 software developed by physicists Les Cowley and Michael Schroeder, I suggest that it was created by a combination of a fog-bow and ice-crystal arcs. Their program is based on a Monte Carlo technique that tracks rays at a specific solar angle through an ensemble of ice crystals, where the shapes and orientations of the crystals can be chosen. My simulation (figure 5b) tracked rays via the various reflections and refractions of light through cylindrical crystals with hexagonal cross-sections and through others that were a slight variation of these.
The Whymper apparition includes the antisolar horizontal arc and central cross, which can occur if the long axes of the hexagonal cylinders become horizontally aligned. Whymper also observed two bright vertical strips that intersected the horizontal arc to create the two vast crosses. I discovered that these features could be created with hexagonal cylinders that were capped with pyramids – a form of ice crystal known to occur at low temperatures. The cylinder axis pointed horizontally, while two of the six sides were oriented vertically.
Taken together with a fog-bow, the computed result is not dissimilar to the picture that appears in Whymper’s The Ascent of the Matterhorn, especially a later sketch that he derived while writing the book (figure 5c). Although the simulation may seem somewhat contrived, a similar alignment of hexagonal cylinders with two opposite hexagonal faces horizontal was required to explain the features of an intricate halo observed by Captain W E Parry in 1820 during his search for the North West Passage.
The glory of glories
Three days after the Matterhorn tragedy, a separate Italian team made the second ascent from the opposite side of the mountain. During their descent – and at about the same time and altitude that the Whymper apparition had been seen – the party found itself above thick cloud when the climbers observed another strange phenomenon. What they saw this time were their own shadows projected onto the cloud, with rainbow-like rings around their own heads. Known as the “Brocken spectre”, the shadow is said to have been named after an incident involving a climber on the Brocken in the Harz Mountains of Germany. Startled by the appearance of his shadow on a cloud, the climber allegedly fell to his death.
The bright, coloured rings are known collectively as a “glory”. Glories are created when light is backscattered from small water droplets in a cloud. It is a complicated process, but one of the major mechanisms occurs when light strikes a spherical water droplet almost tangentially. The light refracts into the drop and is then internally reflected. But rather than refracting out again when it strikes the surface, it can then travel as a surface wave on the droplet, before emerging at the opposite side of the drop at 180° to the direction in which it arrived (figure 6a). The coloured rings are formed when light that has been backscattered in this way from different parts of the droplet edge interferes (H Bryant and N Jarmie 1974 The glory Scientific American July pp60–71).
Glories are not uncommon. While climbing in Snowdonia in north Wales, for example, I and my fellow climbers emerged from a cloud layer into the Sun, where we were greeted by a glory beneath us. At least three orders of interference rings were visible (figure 6b). The rings are much smaller than those of a rainbow but grow bigger as the droplets shrink in size. Distinct glories – like supernumerary rainbows – therefore require a uniform droplet size. A detailed mathematical explanation of the glory only became possible once physicists had worked out how electromagnetic radiation scatters from spheres, the theory of which is usually attributed to Gustav Mie, who published his work in 1908. However, it was not until 1947 that Hendrik van de Hulst suggested the surface-wave interpretation.
6 Gorgeous glories
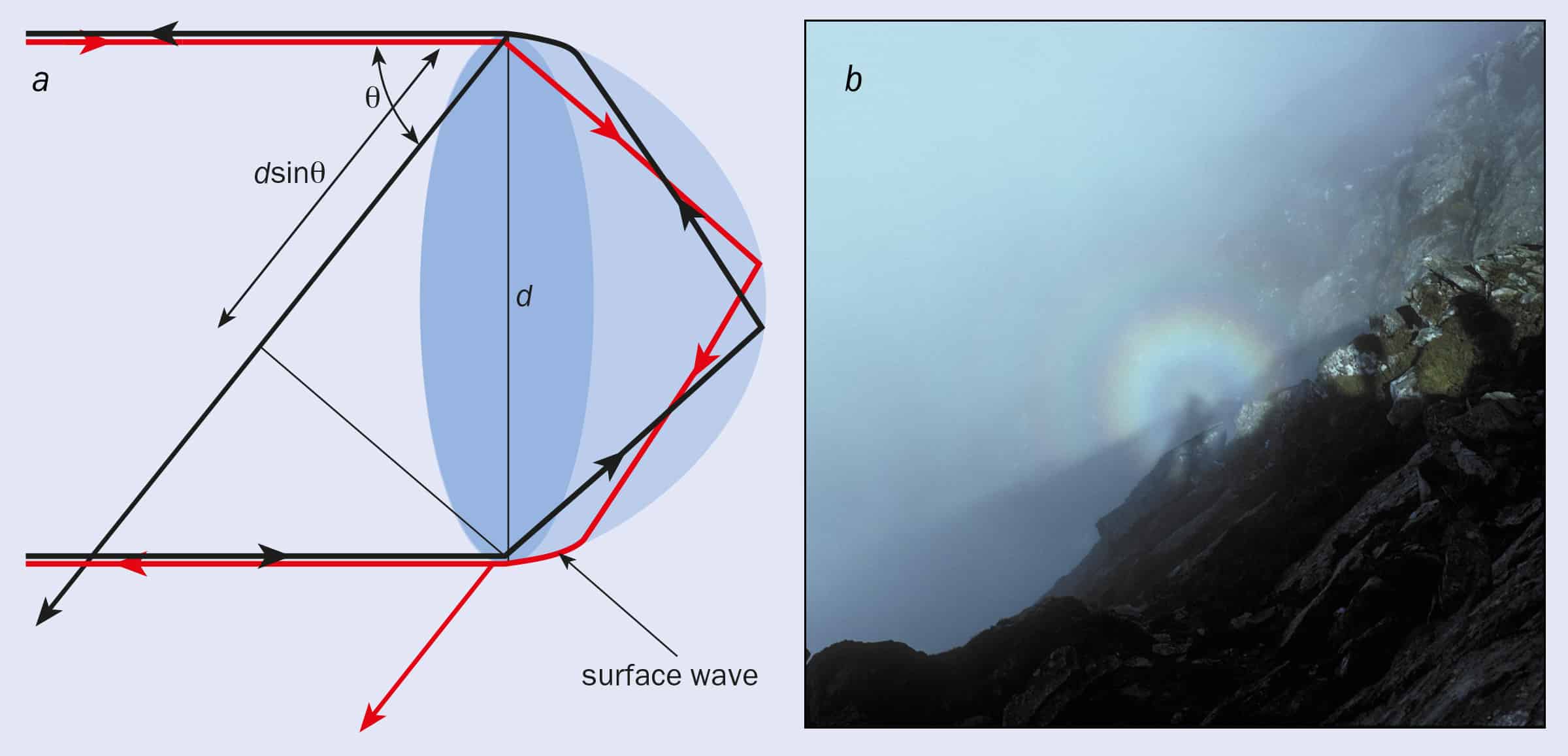 (a) Light rays that strike a water droplet at grazing incidence refract into the droplet before being internally reflected and re-emerging from a surface wave 180° opposite. The edge of the droplet can therefore be considered as a coherent source of light, which means that diffraction from an ensemble of such droplets can produce coloured rings, known as a “glory”. (b) This glory was observed by the author while climbing Pen yr Ole Wen – or “hill of the white light” – in Snowdonia, north Wales, in 1993. Analysis of the photograph shows that the first red ring in the picture is at angle, θ, of about 4° from the antisolar direction. Simple diffraction suggests that sinθ≈λ/d. With red light at wavelength λ= 0.65 µm, the diameter, d, of the droplets that created the glory will be about 10 µm. This agrees well with the typical size of mist droplets.
(a) Light rays that strike a water droplet at grazing incidence refract into the droplet before being internally reflected and re-emerging from a surface wave 180° opposite. The edge of the droplet can therefore be considered as a coherent source of light, which means that diffraction from an ensemble of such droplets can produce coloured rings, known as a “glory”. (b) This glory was observed by the author while climbing Pen yr Ole Wen – or “hill of the white light” – in Snowdonia, north Wales, in 1993. Analysis of the photograph shows that the first red ring in the picture is at angle, θ, of about 4° from the antisolar direction. Simple diffraction suggests that sinθ≈λ/d. With red light at wavelength λ= 0.65 µm, the diameter, d, of the droplets that created the glory will be about 10 µm. This agrees well with the typical size of mist droplets.
Dew-bows at dawn
Another strange optical phenomenon that can occasionally be seen is the “dew-bow”, which was the subject of a letter last year from Physics World reader and golf enthusiast John Wesson (“Golfing beauty”, March 2003). Wesson described a dew-bow that he had seen while out on a golf course early one morning. “Its hyperbolic shape extended into the distance and its vertex was a short distance from my feet,” he wrote. “As I walked forward, my rainbow moved with me – lasting perhaps 15 minutes.”
A dew-bow is created when light refracts from water droplets located on a horizontal plane, such as the grass of a golf course. As with a standard rainbow, the observer can be pictured as standing at the vertex of a cone and receiving the rainbow light from angles along the cone’s surface. The observer interprets the shape of the light source as the cross-section that is cut through the cone by the plane containing the droplets. So if sunlight strikes the plane at a very shallow angle, for example in early morning, the dew-bow has a hyperbolic shape. Later in the day, if the droplets are still present, the dew-bow will become an ellipse.
Wesson asks why, given that dew is so common, are dew-bows so rare? He has only ever seen one dew-bow, despite being a regular on the golf course. If he had seen many dew-bows of different brightnesses, we might conclude that their formation depends on dew density. But I do not think that the density of dewdrops plays the key role. Dew-bows probably form only when spherical water droplets are present. As with a standard rainbow, this allows sunrays to be internally reflected from the back of the drops. However, experiments with a blade of grass suggest that most drops of water attached to grass are not spheres but hemispheres. Internal reflection would therefore not be possible for the range of angles needed for a complete hyperbola to be seen.
In his classic book Light and Colour in the Open Air, which was originally published in 1954, Marcel Minnaert claims that dew-bows can originate from the fine spherical droplets of dew on cobwebs. But spiders make webs every morning, so why are dew-bows not then seen more often? Maybe it depends on the size of the drops. Perhaps dew-bows are formed only if fine spherical dewdrops condense on and cling to the edges or tip (rather than the faces) of blades of grass. The mystery remains.
Keats’ unweaved rainbow
So has cold philosophy unweaved the rainbow? It seems to me that a fuller understanding of the physical basis of this intricate phenomenon can lead to a proper appreciation of it and also shed light on other, yet more subtle effects that lie outside what Keats called the “dull catalogue of common things”. Each rainbow, halo and glory is unique in that each results from a never-to-be-repeated ensemble of raindrops or ice crystals of particular shapes and sizes. Some forms, like the Whymper apparition, are so rare that you will be lucky to ever seen one in your lifetime.
The physics of the rainbow is perhaps like particle physics, in that each deeper explanation reveals yet another mystery. However, unlike particle physics, we have the final word with Mie scattering theory, which as well as explaining the glory gives a complete theory of the rainbow. But questions still persist. Why, for example, are dew-bows so rare? And why does lightning destroy a rainbow? It appears that some subtleties surrounding the rainbow continue to remain a mystery.
- This article first appeared in the February 2004 issue of Physics World. Since then both third-order and fourth-order rainbows have been photographed.