Time crystals break time-translational symmetry rather than spatial symmetry, as ordinary crystals do. Peter Hannaford and Krzysztof Sacha look at how this exotic state could have similar applications to condensed-matter devices

Look at a computer processor or a superconducting device and imagine what’s inside – countless electrons flying between the ions that form a solid-state crystal. Now try to imagine it’s all happening not in space but in the fourth dimension of time. Is it possible that condensed-matter devices and conventional electronics can enter the time dimension?
In 2012 the Nobel-prize-winning physicist Frank Wilczek published his seminal article on “quantum time crystals”, in which he posed the provocative question of whether time-translational symmetry – where one instant in time is equivalent to any other – can be spontaneously broken in the lowest-energy state of a quantum-mechanical system (Phys. Rev. Lett. 109 160401). Such symmetry breaking would lead to the spontaneous emergence of a “time crystal”, just as spontaneous translational symmetry-breaking leads to the formation of an ordinary crystal in space (see “In search of time crystals” by Philip Ball, July 2018),
It was a weird idea, and almost no-one understood it. Indeed, the suggested model turned out to be wrong. That’s because in the thermodynamic limit of a large number of particles, in order to minimize energy, quantum particles prefer to stop, rather than to move, even in the presence of a magnetic field (Phys. Rev. Lett. 111 070402, Phys. Rev. Lett. 119 250602). So it’s not easy to see how particles can spontaneously exhibit periodic motion in time by a self-organization process, like they do in space, while they remain at equilibrium, in the state with the lowest possible energy (Phys. Rev. Lett. 114 251603, Phys. Rev. Lett. 123 210602).
The rise of discrete time crystals
Wilczek’s idea did, however, trigger new thinking about whether there might be other ways that crystalline behaviour could be hosted in the time dimension. In 2015 one of us (Sacha) proposed that a periodically driven (and thus non-equilibrium) quantum many-body system – such as a Bose–Einstein condensate (BEC) of ultracold atoms bouncing on an oscillating atom mirror (figure 1) – can spontaneously break discrete time-translational symmetry, due to interactions between the particles. The atoms would start to evolve with a period twice as long as the period of the driving force, to create what is known as a “discrete” time crystal (Phys. Rev. A 91 033617). Classically, such “period-doubling” of a driven oscillatory system is well known. However, in the quantum world, stationary solutions of the Schrödinger equation must follow the period of the force. If a system spontaneously chooses stationary motion with a different period, the discrete time-translational symmetry is broken. We call the symmetry discrete because not every point in time is equivalent to any other for the periodically changing force. The only points that are equivalent are those that correspond to a discrete jump in time by the period of the force.
1 Bouncing on mirrors
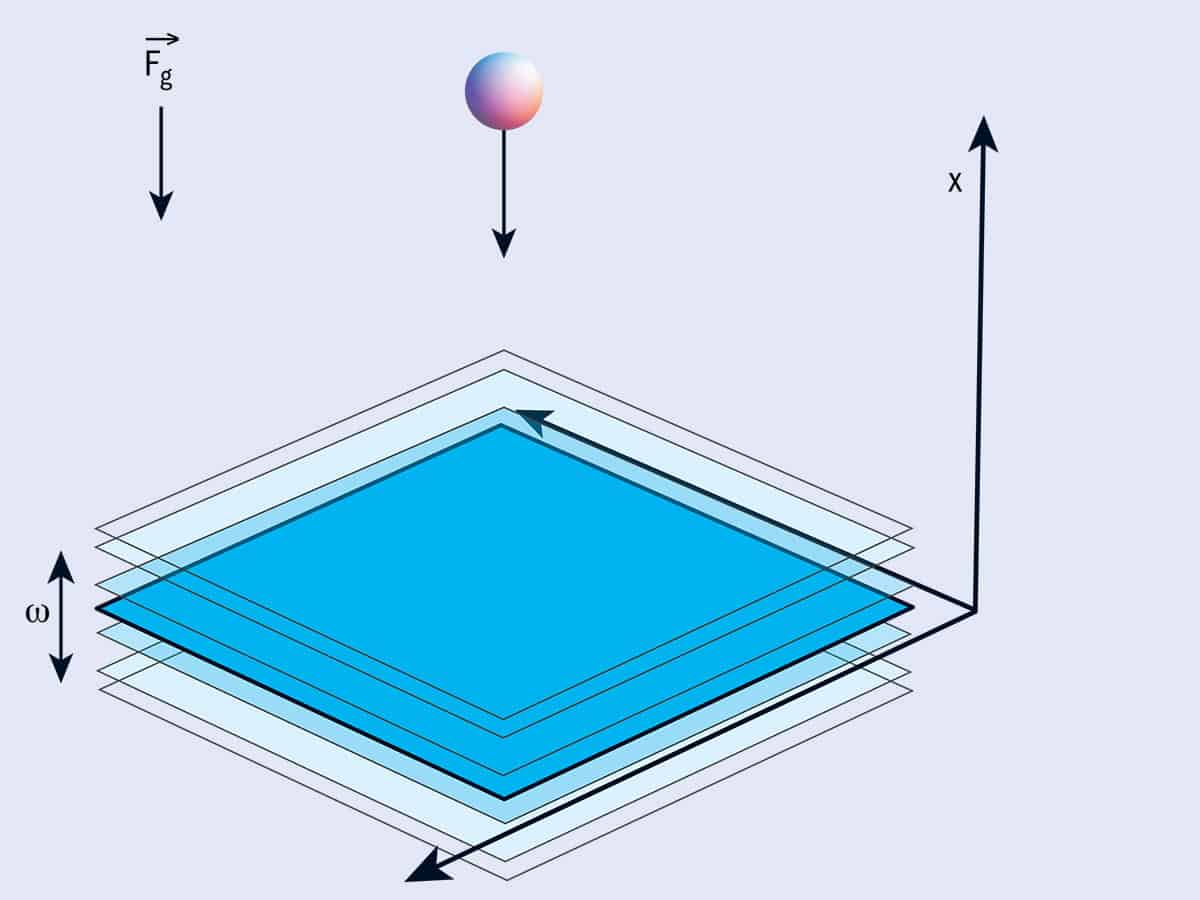 Bouncing ultracold atoms on an oscillating atom mirror (with period T = 2π/ω) is one way of producing a discrete time crystal. The atom mirror could be, for example, a blue-detuned repulsive light sheet (adapted from original figure by Artur Miroszewski).
Bouncing ultracold atoms on an oscillating atom mirror (with period T = 2π/ω) is one way of producing a discrete time crystal. The atom mirror could be, for example, a blue-detuned repulsive light sheet (adapted from original figure by Artur Miroszewski).
Similar ideas were later proposed that involve periodically driven systems of spins, by teams at Princeton University in the US and the Max Planck Institute for Physics of Complex Systems in Germany (Phys. Rev. Lett. 116 250401), and the University of California, Santa Barbara (Phys. Rev. Lett. 117 090402) and Berkeley (Phys. Rev. Lett. 118 030401). These proposals considered a 1D chain of spins – such as a string of ions in electromagnetic traps – which are first prepared in a polarized spin state. The ions are then subjected to a periodic spin-flip driving pulse in the presence of spin–spin interaction and controlled spin disorder, which induces a quantum effect that prevents the system of spins from absorbing energy and heating up. Despite the fact that the driving pulses dictate a certain period, the spin system self-organizes its motion with a period twice as long as the drive. Discrete time crystals break “ergodicity”, according to which a generic periodically driven many-body system should heat up to an infinite temperature. In the proposed spin system, disorder in the presence of particle interaction is expected to be responsible for many-body localization effects, which prevent heat from being freely redistributed and account for the lack of heating.
Within a few months of these initial proposals, preliminary experimental evidence for such discrete time crystals in spin systems was reported by Chris Monroe’s group at the University of Maryland in the US, using a 1D chain of interacting ytterbium-171 ions (Nature 543 217), and by Mikhail Lukin’s group at Harvard University, using 3D ensembles of interacting nitrogen-vacancy spin centres in diamond (Nature 543 221). Similar observations have since been made in NMR experiments by Ganesh Sreejith and colleagues at the Indian Institute of Science Education and Research in Pune, using nuclear spins in organic molecules in solution (Phys. Rev. Lett. 120 180602), and by Sean Barrett and colleagues at Yale University in the US, using phosphorus-31 spins in ordered crystals of ammonium dihydrogen phosphate (Phys. Rev. Lett. 120 180603). In a different kind of system, Peter van der Straten and co-workers at Utrecht University in the Netherlands created a “space–time crystal”, with periodic structure in both space and time (Phys. Rev. Lett. 121 185301). In this experiment a BEC of ultracold sodium-23 atoms was prepared in an elongated trap, and the vibrational motion of the condensate along the radial direction – induced by suddenly changing the radial trap frequency – acted as a driving force. Again, time-periodic oscillations of the atomic density along the longitudinal direction were observed with a period twice the length of the period of the driving force. The atomic density also revealed a spatial periodic structure in the longitudinal direction; in other words, it was a crystal in both space and time.
Ultracold atoms bouncing on an oscillating mirror seem to be much more flexible for realizing discrete time crystals than spin systems do. They could let us create discrete time crystals with dramatic breaking of time-translational symmetry; for example, they can evolve with periods more than an order of magnitude longer than the driving period (Phys. Rev. A 98 013613), thereby creating lots of available “lattice sites” in the time dimension.
Time vs space
Discrete time crystals demonstrate a very important property of solid-state systems: the formation of periodic structures due to spontaneous breaking of translational symmetries. Space crystals can possess a variety of very different and useful properties: they can be insulators, conductors and even superconductors. Can we realize the equivalent of such phenomena in the time dimension?
Take a space crystal that is not perfect because the position of the ions is somewhat random or disordered. If the disorder is sufficiently strong, the electrons can’t form an electric current due to destructive interference between different scattering paths. Instead, they become localized and unable to propagate in space in a way predicted by the physicist Philip Anderson in 1958. But such “Anderson localization” can occur in the time dimension too. To understand why, imagine bouncing a ping-pong ball on a bat. If we were a bad table-tennis player, we’d probably lose the ball because our hand is shaking randomly. However, if the ball were a quantum object – like a BEC of ultracold atoms – quantum mechanics would help us, because the time disorder from our shaking hand would result in Anderson localization in the time dimension (Sci. Reports 5 10787). This is an example of a condensed-matter phenomenon that can be observed in the time dimension when a space crystal is exchanged with a time crystal and disorder in space is substituted by disorder in time (figure 2).
2 Anderson localization
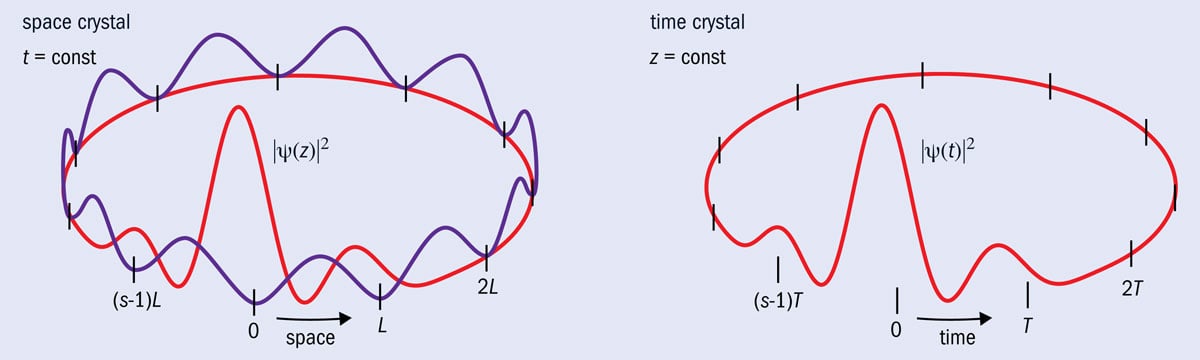 Comparison of the well-known phenomenon of Anderson localization in a 1D space crystal having periodic boundary conditions (a, left) with Anderson localization in the time dimension (b, right). In order to switch from a space crystal to a time crystal we have to exchange the role of space, z, and time, t; that is, we fix the position in space and ask if the probability of the detection of a particle at this point in space |Ψ(t)|2 is Anderson-localized around a certain moment of time.
Comparison of the well-known phenomenon of Anderson localization in a 1D space crystal having periodic boundary conditions (a, left) with Anderson localization in the time dimension (b, right). In order to switch from a space crystal to a time crystal we have to exchange the role of space, z, and time, t; that is, we fix the position in space and ask if the probability of the detection of a particle at this point in space |Ψ(t)|2 is Anderson-localized around a certain moment of time.
In an actual experiment, the probability density of the bouncing ultracold atoms at a particular point in space is recorded, and the atoms appear here with an exponentially localized profile in time (Phys. Rev. A 98 013613). An advantage of studying Anderson localization in the time dimension is that it is relatively straightforward to introduce disorder in a highly controlled way, simply by applying some disorder to the oscillation of the atom mirror. In practice, Anderson localization in the time dimension can be used to control the time of the appearance of a quantum system at a given position by means of a fluctuating force.
Child on a swing
The multidimensionality (3D, 2D or 1D) of space crystals and the interactions between the particles are all elements of condensed-matter systems that physicists can use to build useful devices and to provide scope for inventing novel devices in the future. The analogues of these variables are also available in time crystals – in other words, the degrees of freedom in the time dimension offer an additional “knob” to control the properties of physical systems.
Periodically driven systems have been known for centuries, but not every system perturbed by a periodically changing force would appear to have much to do with condensed-matter systems. For example, a swing driven periodically by a child sitting on it and swinging their legs doesn’t appear to have much in common with an electron moving in a space crystal. But, in fact, there is an analogy between the two. There are resonances when a child on a swing is pushing their legs backwards and forwards with a frequency ω that is an integer multiple of the frequency Ω of the oscillations of the swing (i.e. ω = sΩ, where s is an integer and denotes an s: 1 resonance between the driving force and a system evolving along a periodic trajectory). The behaviour of the swing in the vicinity of the resonant periodic trajectory (the periodic “orbit” in a plot of position against time) is well understood in the theory of dynamical systems. In the reference frame moving with the swing, this behaviour can be described by a model similar to that of an electron in a 1D ring-shaped periodic lattice. For values of s >> 1, in the quantum description, electron energy bands (or more precisely “quasi-energy bands”) form (Phys. Rev. Lett. 111 205303). In other words, a time-periodic crystalline structure is created along a resonant periodic orbit, similar to the periodic lattice in a space crystal.
In space crystals, we usually ask how a system behaves or is structured in space at a given moment of time. In time crystals, we are interested in how a system behaves in time when we focus on its appearance at a given position in space
There is another important property of such a periodic system: any condensed-matter behaviour that we can describe by means of the theory of dynamical systems in the frame moving with the swing is observed in the time domain when we return to the laboratory frame. Thus, in order to observe condensed-matter phenomena in the time dimension, we have to ask the child to push (or drive) resonantly s times faster than the swing’s natural period and we need to stand next to the swing, at some particular position in space, and observe if it is behaving in time like an electron in a space crystal. That is, if we want to switch from space crystals to time crystals we have to exchange the role of space and time. In space crystals, we usually ask how a system behaves or is structured in space at a given moment of time. In time crystals, we are interested in how a system behaves in time when we focus on its appearance at a given position in space. However, condensed-matter phenomena – like an electron in a solid-state system – are described by quantum mechanics. Thus, in order to realize condensed-matter physics in the time dimension, the child needs to drive not a classical swing but a “quantum swing”. This could take the form of any quantum system that in the classical description reveals so-called nonlinear resonances, meaning any periodically driven system except a harmonic oscillator (for which the restoring force is linearly proportional to the displacement). For example, we can exchange the swing with ultracold atoms and the child with a periodically oscillating atom mirror to realize condensed-matter physics in the time dimension (figure 1).
Can we realize non-trivial condensed-matter phases – such as topological insulating phases – in the time dimension? Topological insulators are condensed-matter systems that are insulators in their interior but, by virtue of the topological properties of the electronic structure, have conducting surface (edge) states. They are characterized by global topological invariants. An example of a topological invariant is the number of holes a surface has: a sphere has no holes while a torus has one. It is hard to change such a topological invariant because it is not possible to gradually introduce a hole in a sphere in order to change it to a torus – either there is a hole or there is no hole, but there is nothing like a fraction of a hole. Even the vacuum (empty space) has trivial topological invariants. In order to reconcile a change of this invariant at the interface between the vacuum and a topological insulator, there are surface (edge) states that close the gap between the energy bands of the insulator, thereby producing conducting behaviour.
Can a quantum swing behave like an electron in a topological insulator? Yes, for example if we ask the child to push with a combination of a resonant frequency ω and a sub-harmonic frequency ω/2 (Optica 5 1390, New J. Phys. 21 052003). Then the motion of the swing effectively creates a chain of lattice sites along the resonant orbit with staggered hopping amplitudes, and thus reproduces an example of a topological system, called the Su–Schrieffer–Heeger lattice. In order to observe the edge states, we need to create an “edge” in the motion of the swing and then check if there are quantum states that are localized close to it. How can we create an edge in time? We ask the child to jump on the swing from time to time, which introduces a barrier in the chain of lattice sites along the resonant orbit and consequently breaks the time-translational symmetry along the orbit, similar to how a surface breaks spatial-translational symmetry in an ordinary topological insulator. When we stand next to the swing and the edge of a time lattice is passing by, we can observe that the swing follows the edge if the swing is prepared in a quantum edge state. By contrast, other quantum states of the swing are delocalized along the entire resonant orbit, similar to what bulk states do in ordinary topological insulators.

Classical time crystals could exist in nature, say physicists
In a similar way, we can use ultracold atoms bouncing on an oscillating mirror to create a time-crystal equivalent of a topological insulator (New J. Phys. 21 052003). Spatial topological insulators are currently a hot topic in condensed-matter physics, and they have potential applications in many areas such as electronics, spintronics and quantum computers. We now see that topological insulating phases can also be realized in the time dimension and the playground for novel applications is broadened.
From one to many
So far we have discussed how single-particle condensed-matter phenomena can be realized in the time dimension, which can be demonstrated with the help of a BEC of non-interacting atoms, where the BEC acts like a single quantum entity even though it’s a many-particle system. But is many-body physics of interacting particles available in time crystals? Again, the answer is yes, because time crystals built with interacting ultracold atoms bouncing on an oscillating mirror can be effectively described by the Bose–Hubbard model, which is widely used to describe the dynamics of interacting ultracold atoms trapped in a spatially periodic lattice. Modulating the mirror’s motion lets you control and engineer properties of the Bose–Hubbard model, such as the tunnelling rate of particles between neighbouring temporal lattice sites. Furthermore, the application of a magnetically tunable “Feshbach resonance” – which occurs when two colliding atoms resonantly couple to a molecular bound state – allows the interaction between atoms to be precisely controlled.
Even though ultracold (neutral) atoms interact via a short-range potential, interactions in the effective Bose–Hubbard models that describe time crystals can be long-ranged and, moreover, they can be controlled and engineered. Atoms occupying a given localized wave-packet that is evolving along a resonant trajectory interact via short-range interactions in the effective Bose–Hubbard model. However, additionally, atoms occupying different localized wave-packets also interact because the different wave-packets pass each other during the course of the time evolution along a resonant orbit – such transient interactions between atoms result in long-range interactions in the effective Bose–Hubbard model that describes the resonant bouncing of atoms on an oscillating mirror. Moreover, if the original short-range contact interaction is properly modulated in time, by varying the Feshbach magnetic field, one can control the effective interactions and engineer very exotic long-range interactions not available in nature (Phys. Rev. Lett. 120 140401). Implementation of exotic long-range interactions may allow the realization of novel quantum phases and phenomena that are not attainable in conventional systems with crystalline structures in space. Again, the playground for novel applications becomes broader.
Time is a single degree of freedom, so it’s hard to imagine what multi-dimensional time crystals might be. However, time crystals with the properties of 2D or 3D space crystals can nonetheless be created
Time is a single degree of freedom, so it’s hard to imagine what multidimensional time crystals might be. However, time crystals with the properties of 2D or 3D space crystals can nonetheless be created. If, instead of a single oscillating mirror, we prepare two orthogonal oscillating mirrors with atoms bouncing resonantly between them, the resonant dynamics is described by a Bose–Hubbard model corresponding to 2D time lattices, and 2D condensed-matter phenomena can then be investigated in the time dimension (figure 3). When we place a detector at a certain point between the mirrors, the clicking of the detector in time will reproduce the behaviour of a system along a cut of a lattice described by the Bose–Hubbard model. Different locations of the detector correspond to different cuts of the lattice. Such a detection of system behaviour in time allows one to investigate 2D condensed-matter behaviour that emerges in the dynamics of a driven system.
3 Degrees of freedom
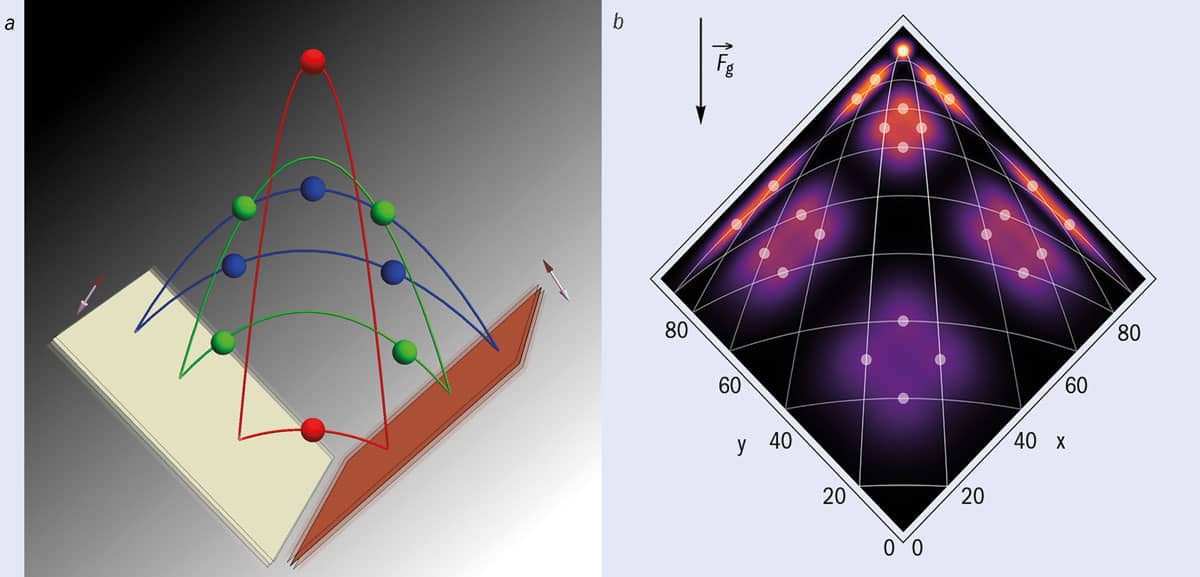 (a) Atoms bouncing resonantly between two orthogonal oscillating mirrors (graphic courtesy: Artur Miroszewski). (b) Single-shot photo of a time lattice which is effectively described by the 2D Bose–Hubbard model (reprinted from Phys. Rev. Lett. 120 140401).
(a) Atoms bouncing resonantly between two orthogonal oscillating mirrors (graphic courtesy: Artur Miroszewski). (b) Single-shot photo of a time lattice which is effectively described by the 2D Bose–Hubbard model (reprinted from Phys. Rev. Lett. 120 140401).
Suitable modulation of the mirror’s motion also allows one to realize not only time crystals but also quasicrystalline structures in time, which exhibit long-range order but without any periodicity. An example of a quasicrystal is the Fibonacci quasicrystal, like the pattern of florets in the head of a sunflower. A 1D Fibonacci quasicrystal can be created when a suitably chosen line cuts a periodic square lattice. It turns out it’s possible to generate either a 1D Fibonacci quasicrystal in time using atoms bouncing on a single oscillating mirror or to observe the spontaneous formation of a Fibonacci sequence in the time dimension by bouncing atoms between a pair of orthogonal oscillating mirrors (Phys. Rev. B 99 220303).
The world of condensed matter is now entering the fourth dimension of time. Not only is this intriguing in its own right, but it also opens possibilities for novel research directions and maybe new applications and devices. Physicists have predicted that time crystals could be used to experimentally realize exotic long-range interactions that are not available in nature or even in the quantum simulation of condensed-matter systems based on ultracold atoms in spatial optical lattices. The realm of “time engineering” has opened. It’s hard to predict what will emerge in the future. Combining crystalline structures in space and in time should allow novel devices to be built, because processes that cannot be performed together in space dimensions can be realized separately in space and time. In other words, some processes can be performed by the internal dynamics of a system where importantly there is also crystalline structure. Crystalline structures in four dimensions should open new possibilities. Is time–space electronics just around the corner?