Dreamt up by the physics Nobel laureate Frank Wilczek in 2012, the notion of “time crystals” is now moving from theory to experiment – and could also lead to applications such as a new kind of atomic clock. Philip Ball explains
There’s no point in denying that the appeal of an idea in science can depend on finding a catchy name for it. Just think of the Big Bang, black holes or dark matter. None of those, however, comes close to the Doctor Who-style resonance of the phrase “time crystals”. But this concept, first proposed in 2012 by the Nobel-prize-winning physicist Frank Wilczek (Phys. Rev. Lett. 109 160401), is more than a case of canny packaging. It toys with some deep themes in physics – the symmetry of time, quantum mechanics and the role of disorder – to come up with a counterintuitive new proposal for how matter can behave.
Ordinary crystals consist of atoms or molecules arranged regularly in space. But rather than having a periodicity in space, time crystals exhibit a periodicity in time. They display a dynamical, ever-changing mode of behaviour that repeats regularly. Although Wilczek’s original concept of time crystals as materials that show spontaneous temporal periodicity has been invalidated, it’s possible to produce a variant of what he had in mind by driving a system out of equilibrium. Last year time crystals of this other kind were demonstrated for the first time in the lab. And very recently two more varieties have been spotted, raising the possibility that time-crystal behaviour might be a rather common property of materials.
That’s all very well, but are time crystals actually of any use? Some researchers think they could be used to make highly sensitive magnetic-field detectors or possibly even components of quantum computers. Their real value, however, could be to furnish a broader picture of how condensed states of matter can behave. For theorists exploring that question, says Norman Yao of the University of California at Berkeley, “all of a sudden we have a new playground”.
Time for a break
To understand time crystals, let’s remind ourselves about ordinary crystals. Diamond, say, breaks spatial symmetry because not every location is equivalent. Some locations have carbons atoms; others don’t. If you shift, or “translate”, the diamond lattice by some arbitrary amount, it won’t superimpose on the original lattice; the crystal structure has broken the translational symmetry of uniform space. But if you shift the lattice by some integer multiple of the spacing between atoms, it does superimpose, which means that the broken translational symmetry is periodic.
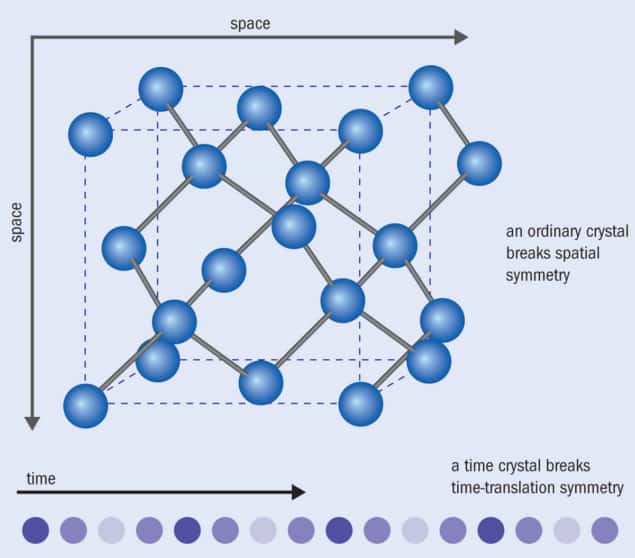
But what if a material could break “time-translation” symmetry – the symmetry that makes the system unchanged if you shift it forward by an arbitrary amount of time? In his original 2012 proposal, Wilczek considered a ring of quantum particles – the simplest 1D system without edges. He asked if there might be circumstances in which the lowest-energy state of this ring breaks time-translational symmetry such that it changes in time, but returns to the original state at periodic intervals (figure 1).
If a system could indeed break time symmetry, Wilczek reasoned, that periodic change might not necessarily entail the motion of the atoms themselves. Instead, it could perhaps be a periodic cycling of some other property, such as the orientation of their spins. Just as moving through space in an ordinary crystal seems to take you away from and then back to where you started – you come to another atom identical to the one you began at – so moving through time at some location in a time crystal will trigger a periodic departure from and return to your initial state.
Such spontaneous, continual change sounds “perilously close to fitting the definition of a perpetual motion machine”, Wilczek admitted in his 2012 paper. But it needn’t actually be that. After all, we already know of one type of quantum-mechanical ground state that supports a kind of motion indefinitely: a current circulating forever around a ring of superconducting material. But that’s uniform motion. In a time crystal, the motion would oscillate – like, say, a Mexican wave of flipped spins circulating around Wilczek’s ring of spins forever.
Question time
So far so good for time crystals, but in 2015 physicists Haruki Watanabe from the University of California, Berkeley, and Masaki Oshikawa from the University of Tokyo argued that the idea won’t stack up. They showed that no physical system in its lowest-energy state can form a time crystal of the kind envisaged by Wilczek (Phys. Rev. Lett. 114 251603). A similar objection had been previously stated more briefly by Patrick Bruno of the European Synchrotron Radiation Facility in Grenoble, France (Phys. Rev. Lett. 110 118901).
The argument against time crystals is that there is no way to prevent such an oscillating system from dissipating energy, meaning that the oscillating state must gradually decay – it’s not in equilibrium. Systems in thermal equilibrium cannot therefore have any interesting time dependencies – there will be nothing interesting that changes with time. So were time crystals just the futile fantasy of a Nobel-prize-winning theorist?
Not quite. Watanabe and Oshikawa admitted that there is a loophole in their argument against the existence of time crystals. Periodic “time-crystal” behaviour could exist, they said, in a system that is pushed out of equilibrium by some driving force. In effect, says David Huse of Princeton University, Watanabe and Oshikawa showed that to break time symmetry (and so get time-crystal behaviour) you’d also have to break some other symmetry too, as with a periodic driving force.
The fact that you could get time-periodic behaviour out of equilibrium might not seem that surprising. After all, oscillatory non-equilibrium states are well known already, as Watanabe and Oshikawa pointed out. Such states occur, for example, in the population cycles of ecosystems and in oscillating chemical reactions such as the well-known “clock reaction”, which can keep switching states (and colours) indefinitely if continuously supplied with fresh reagents.
Given that such states exist, they shouldn’t be awarded this fancy new label of time crystals “without a further justification”, the two physicists warned. And in fact, quantum systems subject to some periodic driving force had been thought about long before Wilczek came to the idea of time crystals. They belong to a broader class known as “Floquet systems”, named after the 19th-century French mathematician Gaston Floquet who worked out the maths needed to analyse them.
A discrete business
In one of those delightful “something in the air” convergences that science occasionally produces, the states that Floquet systems can adopt were being clarified at just the same time as, but independently of, the notion that such non-equilibrium time crystals can exist. In 2016 a team at Princeton and at the Max Planck Institute for the Physics of Complex Systems in Dresden, Germany, showed that Floquet systems containing disorder can, paradoxically, give rise to phases that are periodically ordered in time (Phys. Rev. Lett. 116 250401).
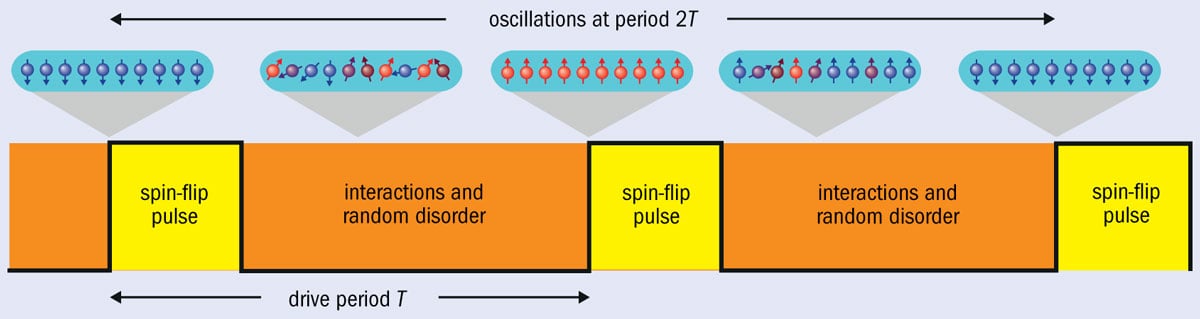
Those researchers considered chains of spins, rather like opened-out versions of Wilczek’s ring of interacting quantum particles. “The authors didn’t notice the connection to Wilczek’s time-crystal discussion,” says Huse, but that was soon pointed out by others – specifically by Chetan Nayak of Microsoft Research in Santa Barbara and co-workers (Phys. Rev. Lett. 117 090402), who also proposed how they might be created (figure 2). Yao and colleagues subsequently dubbed these non-equilibrium states “discrete time crystals”, or DTCs (Phys. Rev. Lett. 118 030401). The “discrete” comes from the fact that their periodicity is a discrete, integer multiple of the driving period.
Discrete time crystals are very subtle. These systems look like they’re in equilibrium, but they’re not really
Chris Monroe, University of Maryland
Despite the reservations of Watanabe and Oshikawa, there is something odd about DTCs in Floquet systems that makes them different from chemical waves or other periodic non-equilibrium states. Although they are being energetically driven, they don’t actually absorb and dissipate any of that energy. “It’s a very subtle concept,” says physicist Chris Monroe of the University of Maryland. “These systems look like they’re in equilibrium, but they’re not really.”

A local affair
This ability to be driven without absorbing energy arises because the disorder in the system makes the energy states isolated from one another. Unable to exchange energy, the system cannot therefore equilibrate. Instead, it gets trapped or “localized” in a particular non-equilibrium state (Ann. Rev. Cond. Matt. Phys. 6 15). This strange situation, dubbed “many-body localization”, goes back to work on disordered systems in the late 1950s by Philip Anderson, who would later go on to win a physics Nobel prize.
Many-body localization, says Huse, arises because of the quantized nature of the energy levels. “If you drive it at a particular frequency, this drive will not be exactly resonant with any energy differences and the system may remain localized and fail to steadily absorb energy from the drive,” he says. That’s crucial, says Yao, because if the system absorbs energy then it slowly heats up until eventually it’s so hot that any possibility of well-ordered phases vanishes.
Such behaviour seemed to require two key ingredients: some disorder among the components, and strong interactions linking their behaviour. That made Monroe think about the kinds of systems in which he specializes: ions held in electromagnetic traps. He and others have manipulated such ions as quantum bits (qubits) for quantum computing, with binary information encoded in their energy levels.
Actually, such systems are rather too perfect, says Monroe: to get DTC behaviour, they needed to inject some disorder in their ion arrays, “making each ion qubit a little different from the others”. It’s precisely because they could introduce this in a controlled way that the trapped ions seemed such an ideal test-bed for comparing with other disordered Floquet systems in which there is more messy, uncontrolled disorder.
Time crystals in the lab
Last year Monroe and his coworkers reported the characteristic signature of a DTC in an array of 10 ytterbium ions held in a trap, where their spins interact with one another (Nature 543 217). When they drove the system with laser pulses to excite transitions between the spin states of the ions, the spin orientation of each atom in the chain started oscillating with a period that was an integer multiple of the driving period. And, crucially, this response frequency is robust. These are the signs of a DTC, says Monroe. “You drive the system in time in a way that’s a bit wobbly, not clean, but it always responds in the same way.”
At the same time, a team at Harvard University led by Mikhail Lukin saw another way to create a quantum system with the requisite disorder: it could come from impurities distributed randomly in a diamond crystal lattice. Lukin and colleagues described a DTC made from coupled electron spins present in defects composed of a nitrogen atom next to a vacant lattice site in diamond at room temperature (Nature 543 221). They used microwaves to manipulate and drive the spin states – basically the procedure used for electron spin resonance (ESR) spectroscopy – in a 300 nm-diameter region of a microscopic beam made of diamond. “It was not fully clear if the DTC phase could even exist in our system,” says Lukin. “But we discovered experimentally that this phase not only exists, but is also remarkably robust.”
We discovered experimentally that discrete time crystals not only exist, but that this phase is also remarkably robust
Mikhail Lukin, Harvard University
The class of materials that act as DTCs has been recently broadened. Earlier this year Ganesh Sreejith and colleagues from the Indian Institute of Science Education and Research in Pune reported it in the interacting nuclear spins of hydrogen, carbon and silicon atoms in three star-shaped organic molecules in solution, probed by nuclear magnetic resonance (NMR) spectroscopy (Phys. Rev. Lett. 120 180602). Given the previous work on spin resonance in diamond defects, says Sreejith, “NMR systems were in some sense a natural place to look for the same physics”.
They saw the tell-tale signature of a DTC phase in the way that the oscillation period of the spins is twice that of the driving pulses. And again, says Sreejith, “the oscillation time period is stable against changes in the pulse properties and other perturbations”. These results, he concludes, “indicate that the phenomena can be observed in simpler systems than what has been studied previously”.

Sean Barrett at Yale University and his colleagues had much the same idea of using NMR, in their case to look at crystals of the salt ammonium dihydrogen phosphate (ADP). When they heard about the earlier experiments last year, Barrett explains, “just by chance we had a nice crystal of ADP already under study in our NMR spectrometer for a completely different purpose, to do with magnetic-resonance imaging of bones”. They have seen DTC behaviour by driving transitions in the phosphorus spins using a sequence of radio-frequency pulses (Phys. Rev. Lett. 120 180603 and Phys. Rev. B 97 184301).
Yao says it’s possible that these NMR systems might prove to be only transient time crystals, since they are expected to eventually relax to thermal equilibrium over long timescales – a process still to be understood. Importantly, however, neither the ADP crystals nor the star-shaped molecules studied by the Pune group have much disorder. “So either many-body localization is a broader phenomenon than previously thought, or it is not required for DTC signatures to be seen,” says Barrett. “I think theorists are working hard to understand what this means.”
This notion of DTCs that don’t depend on disorder is already out there, says Monroe. What you need is merely enough complexity in the interactions. Under certain conditions such a system can never relax to an equilibrium state: a phenomenon called pre-thermalization. Monroe is now seeing if it can be realized with his trapped-ion qubits.
Practical applications
The ability to get such a regular and robust time response out of a disordered system could ultimately point to applications. “In these very messy natural systems with disorder, to have a property emerge that is very stable could point the way to some kind of clock, for example,” Monroe says. Barrett seconds that idea. “The DTC oscillations that all four experiments see is a case where regularly applied pulses make densely packed atoms or spins seem to behave as a synchronized unit,” he says. “If we can understand this behaviour better, then it might be used to improve quantum technologies like atomic clocks.”
If we can understand this behaviour better, then it might be used to improve quantum technologies like atomic clocks
Sean Barrett, Yale University
It would be poetically satisfying if time crystals were to let us measure time more reliably. But Lukin thinks that DTCs might instead be put to a different use, which is that the quantum states between the coupled particles in these systems are so robustly entangled. That means they not only resist the “decoherence” that usually breaks down such states but are also highly sensitive to perturbations such as magnetic fields. They could therefore be used to make tiny magnetic sensors: the more particles there are in the entangled group, the better the sensitivity. Indeed, Lukin, Yao and their collaborator Soonwon Choi reckon that sensors like this could be made either from nitrogen-vacancy defects in diamond or other defects (such as carbon-13 atoms) in layered materials such as graphene (arXiv:1801.00042).
Yao sees another enticing possible application too. Researchers at Microsoft and elsewhere are currently trying to make qubits for quantum computing from quantum states that are rendered stable by “topological protection”: fundamental geometric constraints on the many-body states that would give rise to robust topological qubits. So far, though, making them demands extremely low temperatures, of the order of millikelvins. But Yao says that Floquet phases of DTCs could offer the same benefits at higher temperatures.

Time traders
In fact, he has an even bolder notion: to make DTCs that aren’t quantum mechanical at all, but are governed by classical physics (arXiv:1801.02628). Yao and his coworkers have shown that even in that case, a combination of noise-induced disorder and strong interactions between the components can be enough to induce time-periodic behaviour characteristic of a DTC in a chain of classical particles – balls coupled by springs, say – subject to an oscillatory driving force. Looked at this way, time crystals could have been discovered with the mechanics of the 18th century.
And that’s what’s really exciting about time crystals, Yao says. They show things are possible that you might never have imagined could be. There have even been suggestions of more exotic structures too, such as time quasicrystals and superfluid time crystals (Phys. Rev. Lett. 120 215301). Given the wealth of such paradoxical and surprising substances, time crystals are surely entirely worthy of their Doctor Who style name.